Вступительное испытание по физике в МФТИ

Автор

Четверг, 14 сентября, 2017

В данной статье представлен разбор демонстрационного варианта вступительного испытания по физике в МФТИ. Все решения выполнены профессиональным репетитором по физике и математике, занимающимся подготовкой абитуриентов к поступлению в МФТИ. Представлен также видеоразбор одного из заданий. Статья будет интересна абитуриентам, готовящимся к вступительному испытанию по физике в МФТИ, школьникам и преподавателям, а также всем, кто интересуется решением сложных задач по физике из школьного курса.

Разбор вступительного испытания по физике в МФТИ

1. Шарик скользит по гладкой горизонтальной поверхности и сталкивается с неподвижным шариком. Удар центральный, упругий. После столкновения первый шарик движется назад с кинетической энергией в 9 раз меньшей его начальной кинетической энергии.

1) Найти отношение масс шариков.
2) Найти отношение скорости второго шарика к начальной скорости первого шарика.

Пусть m_1 и m_2 — массы первого и второго шаров, соответственно; \upsilon_1 и \upsilon_2 — скорости движения первого шарика до и после удара, соответственно; u — скорость движения второго шарика после удара.

Определяющая формула кинетической энергии выглядит следующим образом:

    \[ E_K=\frac{m\upsilon^2}{2}. \]

То есть кинетическая энергия пропорциональна квадрату скорости движения тела. Из этого следует, что поскольку после столкновения кинетическая энергия первого шарика стала в 9 раз меньше, то скорость его движения уменьшилась в 3 раза. То есть \upsilon_2 = \frac{1}{3}\upsilon_1.

Запишем закон сохранения импульса в результате столкновения:

    \[ m_1\upsilon_1 = -m_1\upsilon_2+m_2 u. \]

Минус в выражении справа от знака равенства возникает из-за того, что после столкновения первый шарик начинает двигаться в противоположную сторону. После преобразований получаем следующее уравнение:

    \[ \frac{4}{3}m_1\upsilon_1=m_2 u. \]

Из этого уравнения выражаем скорость движения второго шарика после столкновения u через скорость движения первого шарика до столкновения \upsilon_1:

(1)   \begin{equation*} u = \frac{4m_1}{3m_2}\upsilon_1. \end{equation*}

Поскольку удар был упругий, то выполняется закон сохранения механической энергии:

    \[ \frac{m_1\upsilon_1^2}{2}=\frac{1}{9}\cdot\frac{m_1\upsilon_1^2}{2}+\frac{m_2 u^2}{2}. \]

Или после упрощения:

    \[ \frac{8}{9}m_1\upsilon_1^2 = m_2 u^2. \]

Используя уравнение (1), получаем следующий результат:

    \[ \frac{8}{9}m_1\upsilon_1^2 = m_2\cdot \frac{16m_1^2\upsilon_1^2}{9m_2^2}. \]

Далее после несложных преобразований получаем ответ на вопрос под буквой а):

    \[ \frac{m_1}{m_2} = \frac{1}{2}. \]

Далее, используя уравнение (1), получаем ответ на вопрос под буквой б):

    \[ \frac{u}{\upsilon_1} = \frac{4m_1}{3m_2} = \frac{4}{3}\cdot\frac{1}{2} = \frac{2}{3}. \]

2. Идеальный газ является рабочим веществом тепловой машины, работающей по циклу Карно. КПД цикла равен \eta. Найти отношение модуля работы газа при изотермическом сжатии к работе газа за цикл.

Пусть A — работа газа за цикл, A_2 — модуль работы газа при изотермическом сжатии, Q_1 — количество теплоты, переданное газу от нагревателя в процессе изотермического расширения, Q_2 — количество теплоты, отданное газом холодильнику в процессе изотермического сжатия.

В соответствии с 1-ым законом термодинамики имеет место равенство:

    \[ Q_2 = A_2, \]

так как теплота отдаётся холодильнику только в процессе изотермического сжатия газа, при этом изменение внутренней энергии идеального газа равно нулю, поскольку его температура не меняется (процесс изотермический).

Тогда по закону сохранения энергии получаем:

    \[ Q_1=A+Q_2 = A+A_2. \]

Распишем теперь КПД тепловой машины. По определению — это отношение полезной работы (полной работы газа за цикл A) к затраченной энергии (количеству теплоты, которое было передано газу от нагревателя Q_1):

    \[ \eta = \frac{A}{Q_1} = \frac{A}{A+A_2}. \]

Из последнего получаем:

    \[ \frac{1}{\eta} = 1+\frac{A_2}{A}. \]

Выражая искомое отношение, получаем окончательно:

    \[ \frac{A_2}{A} = \frac{1}{\eta}-1 = \frac{1-\eta}{\eta}. \]

3. Параметры цепи указаны на схеме. Источник идеальный. Ключ замыкают.

Электрическая схема из задачи №3 вступительного экзамена по физике в МФТИ

1) Найти установившееся напряжение на конденсаторе.
2) Найти ток через источник сразу после замыкания ключа.
3) Найти ток через источник в момент, когда напряжение на конденсаторе станет E/4.

1) После замыкания ключа через некоторое время конденсатор зарядится и ток через него прекратится. Далее ток будет течь только по «верхней» части схемы (через два последовательно соединённых резистора с сопротивлениями R и 2R, а также источник E с нулевым внутренним сопротивлением). Ток в такой цепи по закону Ома для полной цепи будет равен:

    \[ I_1 = \frac{E}{3R}. \]

Тогда напряжение на конденсаторе будет равно напряжению на резисторе 2R, посrольку они соединены параллельно. То есть искомое напряжение в первом случае будет равно:

    \[ U_1=I_1\cdot 2R = \frac{2E}{3}. \]

2) В самый первой момент после замыкания ключа конденсатор не заряжен и накоротко замыкает резистор 2R, поэтому последний не оказывает сопротивления току. Сопротивление оказывает только резистор R. То есть ток в этот момент равен:

    \[ I_2 = \frac{E}{R}. \]

3) В тот момент, когда напряжение на конденсаторе равно E/4, такое же напряжение наблюдается и на резисторе 2R, и на верхнем участке цепи, поскольку все они соединены параллельно. То есть для «верхней» ветки цепи, состоящей из источника E и резистора сопротивлением R, соединённых последовательно, имеет место следующее равенство:

    \[ \frac{E}{4} = E-I_3R. \]

Примечание: иначе можно сказать, что последнее выражение представляет собой запись 2-го правила Кирхгофа для «верхнего» контура, состоящего из источника E, а также двух резисторов R и 2R.

Из этого уравнения получаем:

    \[ I_3 = \frac{3E}{4R}. \]

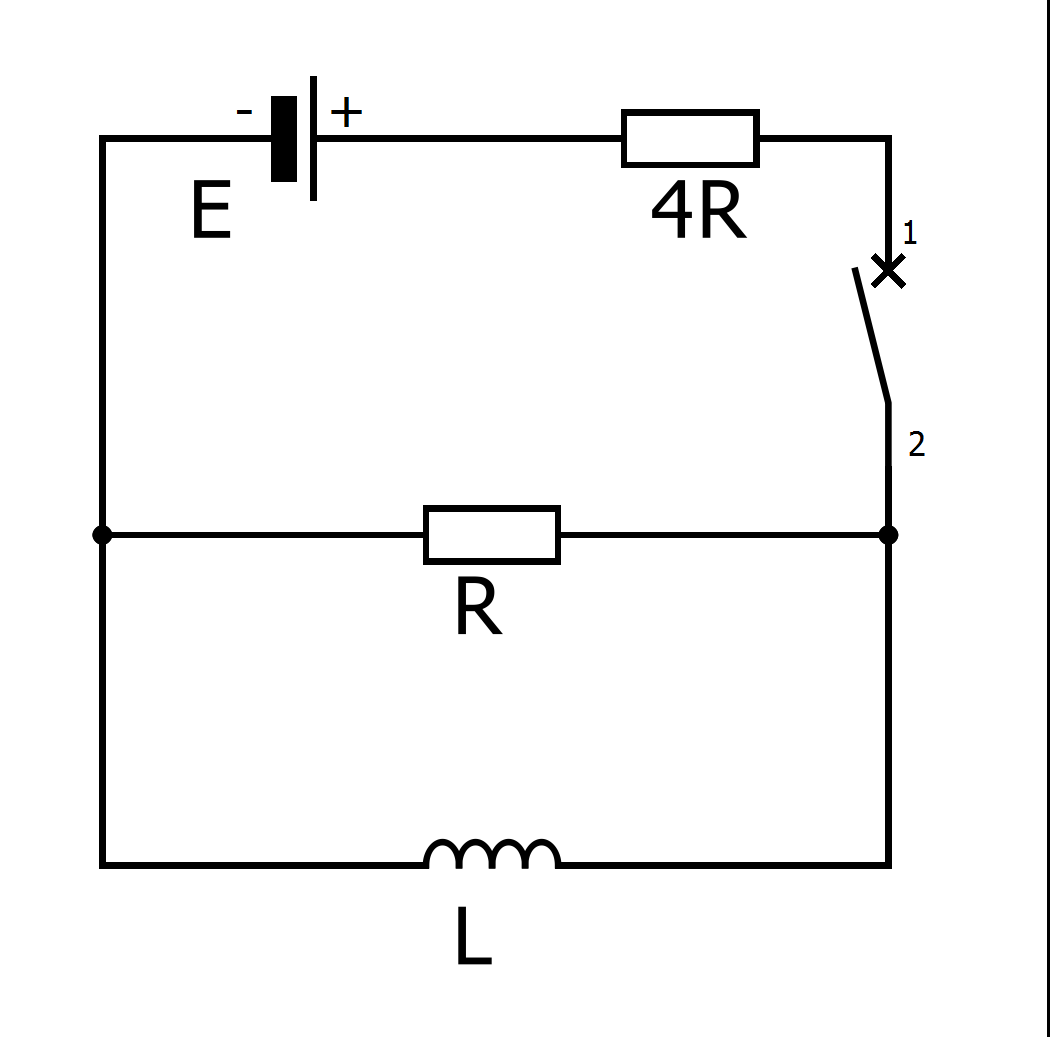
4. В электрической цепи, схема которой показана на рисунке, все элементы идеальные, их параметры указаны. До замыкания ключа ток в цепи отсутствовал. Ключ на некоторое время замыкают, а затем размыкают. Оказалось, что ток через резистор R непосредственно перед размыканием ключа в 3 раза меньше, чем сразу после размыкания.

Электрическая схема из примера вступительного экзамена по физике в МФТИ

1) Найдите ток через резистор R сразу после замыкания ключа.
2) Найдите ток через катушку сразу после размыкания ключа.
3) Какое количество теплоты выделится в цепи после размыкания ключа.

1) Индуктивность — наиболее инерционный элемент электрической цепи, поэтому сразу после замыкания цепи ток через индуктивность будет отсутствовать и затем начнёт постепенно нарастать. То есть в момент сразу после замыкания ключа ток будет протекать только по «верхней» части схемы (через источник и резисторы, соединённые последовательно). То есть ток через резистор R в этом случае равен току во всей цепи и равен:

    \[ I_1 = \frac{E}{5R}. \]

2) Очевидно, что после замыкания ключа экспериментатор не дождался, пока ток в цепи установится, то есть разомкнул ключ до этого момента. Однако, после размыкания ключа, ток через катушку не может уменьшится до нуля мгновенно из-за того, что у катушки есть отличная от нуля индуктивность. В этом смысле катушка в цепи ведёт себя как КАМАЗ (или любой другой тяжёлый грузовик) на дороге, который, разогнавшись до большой скорости, остановиться мгновенно не сможет из-за своей большой массы. То есть индуктивность — это некий аналог массы в механике.

То есть сразу после того, как ключ разомкнут, ток I_2, который до этого тёк через катушку, станет течь в «нижней» части цепи (из последовательно соединённого резистора R и катушки индуктивности L). Этот ток нам и нужно найти. Из условия известно, что этот ток в три раза больше тока, который протекал через резистор R непосредственно перед размыканием. Отметим также, что в соответствии с 1-м правилом Кирхгофа ток через резистор 4R в момент непосредственно перед размыканием ключа равен сумме токов I_2 (ток через катушку L) и \frac{1}{3}I_2 (ток через резистор R). Тогда можно записать 2-е правило Кирхгофа для «верхнего» контура в момент непосредственно перед размыканием ключа:

    \[ E=\left(I_2+\frac{1}{3}I_2\right)\cdot 4R+\frac{1}{3}I_2\cdot R. \]

После несложных преобразований получаем искомое значение тока:

    \[ I_2 = \frac{3}{17}\frac{E}{R}. \]

3) По закону сохранения энергии количество теплоты, которое выделится на резисторе R после размыкания ключа равно запасу энергии, которым будет обладать катушка в момент непосредственно перед размыканием ключа:

    \[ Q = \frac{LI_2^2}{2} = \frac{9}{578}\frac{LE^2}{R^2}. \]

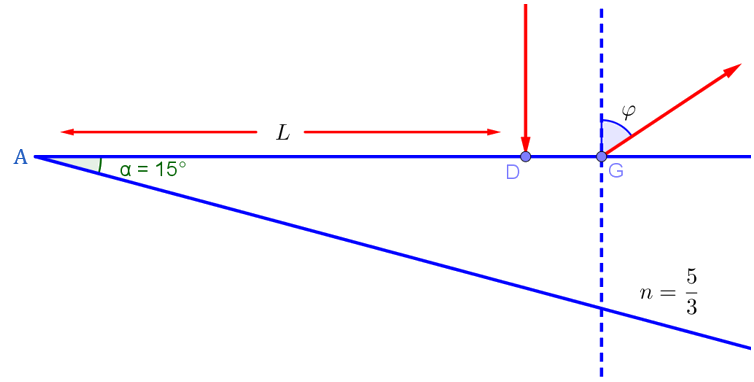
5. Угол при вершине стеклянного клина α = 15ᵒ, показатель преломления стекла n = 5/3. Луч света падает по нормали на верхнюю поверхность клина на расстоянии L от ребра клина (см. рис.). После отражения от нижней зеркальной поверхности клина и преломления на верхней луч выходит из клина под некоторым углом φ к нормали.

Задача по геометрической оптике из вступительного экзамена по физике в МФТИ

1) Найти угол φ.
2) Найти расстояние между точкой выхода луча из клина и ребром клина.


Изобразим оптический ход луча при его прохождении сквозь клин:

Оптический ход луча при его прохождении по стеклянному клину

1) В треугольниках AFE и EDF равны по два угла: ∠F — общий, ∠AEF = ∠FDE = 90º. Значит, оставшиеся два угла также равны. То есть ∠A = ∠DEF = 15º. По закону отражения ∠DEF = ∠FEG = 15º. Значит, ∠DEG = 30º. Кроме того, ∠DEG = ∠η = 30º, так как эти углы являются накрест лежащими при параллельных прямых.

По закону преломления луча в точке G имеет место равенство:

    \[ \frac{\sin\eta}{\sin\varphi} = \frac{1}{n}=\frac{\sin 30^{\circ}}{\sin\varphi}\Rightarrow\frac{1}{2\sin\varphi}=\frac{3}{5}. \]

Понятно, что угол \varphi — острый, поэтому из последнего равенства находим \varphi = \arcsin\frac{5}{6}.

2) Наша цель состоит в нахождении расстояния AG. Ищем сперва расстояние ED из треугольника ADE:

    \[ ED = L\tan 15^{\circ}=L\left(2-\sqrt{3}\right). \]

Доказательство того, что \tan 15^{\circ}=2-\sqrt{3} предлагаю читателю провести самостоятельно, либо посмотреть в видеоразборе выше.

Ищем теперь расстояние DG из треугольника EDG:

    \[ DG = DE\tan 30^{\circ} = L\frac{2-\sqrt{3}}{\sqrt{3}}. \]

Окончательно, находим расстояние AG:

    \[ AG = AD + DG = L + L\frac{2-\sqrt{3}}{\sqrt{3}} = \frac{2L}{\sqrt{3}}. \]

Подготовка к вступительному испытанию по физике в МФТИ

Если вам требуется подготовка к вступительному испытанию по физике в МФТИ, наиболее эффективным способом являются индивидуальные занятия с профессиональным репетитором по математике и физике в Москве, который специализируется на подготовке к этому экзамену. Контакты репетитора вы можете найти на этой странице. Удачи вам и успехов в подготовке к вступительному испытанию по физике в МФТИ!

Метки: , , , ,
Опубликовано в категории Методическая копилка | 2 комментария »

Комментарии

  1. Наталья:
    07.05.2018 в 21:40

    Добрый день.
    Проверьте пжта в 5й задаче у Вас опечатка скорее всего.последняя строчка-должно быть AG=AD+DG=L+L (2-корень из 3/корень из 3), тогда ответ получается.
    Спасибо.

    1. Сергей:
      08.05.2018 в 06:43

      Добрый день, да, исправил это. Спасибо!