Очень часто среди заданий ЕГЭ, вступительных экзаменов и олимпиад по математике встречаются задачи, в которых каким-либо образом задаётся положение корней уравнений с параметром на числовой оси и требуется найти все возможные значения параметра, при которых имеет место такое расположение. Данная статья посвящена разбору нескольких заданий такого рода.
|
Пример 1. Найдите все значения параметра |
Пусть ![]() — квадратичная функция, графиком которой является парабола. Поскольку коэффициент при
— квадратичная функция, графиком которой является парабола. Поскольку коэффициент при ![]() в уравнении равен
в уравнении равен ![]() , то ветви этой параболы направлены вверх. Корни уравнения с параметром — это точки, в которых данная парабола пересекает ось OX. Значит, для выполнения заданного условия парабола должна быть расположена относительно оси OX условно следующим образом:
, то ветви этой параболы направлены вверх. Корни уравнения с параметром — это точки, в которых данная парабола пересекает ось OX. Значит, для выполнения заданного условия парабола должна быть расположена относительно оси OX условно следующим образом:
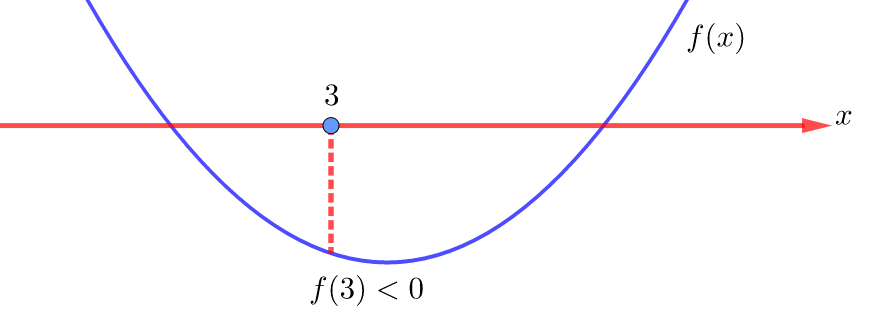
Из рисунка видно, что для выполнения заданного условия необходимо и достаточно, чтобы значение введённой функции было отрицательным в точке ![]() , то есть
, то есть ![]() . Ну действительно, поскольку ветви параболы направлены вверх, то в таком случае она пересечёт ось OX в двух точках, одна из которых находится правее точки
. Ну действительно, поскольку ветви параболы направлены вверх, то в таком случае она пересечёт ось OX в двух точках, одна из которых находится правее точки ![]() , а другая — левее. Итак, имеет место неравенство:
, а другая — левее. Итак, имеет место неравенство:
![]()
![]()
![]()
Ответ: ![]() .
.
|
Пример 2. Найдите все значения параметра |
При ![]() получаем уравнение
получаем уравнение ![]() , которое имеет единственный корень
, которое имеет единственный корень ![]() , поэтому этот случай нам не подходит. Для
, поэтому этот случай нам не подходит. Для ![]() можно поделить обе части данного уравнения на
можно поделить обе части данного уравнения на ![]() . Тогда мы приходим к следующему уравнению:
. Тогда мы приходим к следующему уравнению:
![]()
Теперь мы уверены, что ветви соответствующей параболы направлены вверх, и поэтому мы свели задачу к предыдущей. Пусть ![]() . Тогда требуемое условие будет выполнено тогда и только тогда, когда значение введённой функции в точке
. Тогда требуемое условие будет выполнено тогда и только тогда, когда значение введённой функции в точке ![]() отрицательно, то есть
отрицательно, то есть ![]() :
:
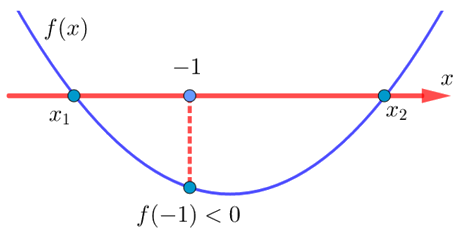
Ну действительно, если ветви параболы направлены вверх, и в точке ![]() она принимает отрицательное значение, то ось OX эта парабола будет пересекать в двух точках
она принимает отрицательное значение, то ось OX эта парабола будет пересекать в двух точках ![]() и
и ![]() , одна из которых находится правее
, одна из которых находится правее ![]() , вторая – левее. Эти точки представляют собой корни уравнения с параметром, которое записано в условии. Тогда точка
, вторая – левее. Эти точки представляют собой корни уравнения с параметром, которое записано в условии. Тогда точка ![]() окажется как раз между корнями уравнения, что нам и нужно. Значит, имеет место неравенство:
окажется как раз между корнями уравнения, что нам и нужно. Значит, имеет место неравенство:
![]()
![]()
![]()
Ответ: ![]() .
.
|
Пример 3. Найдите все значения параметра |
Исследуем сразу случай, когда ![]() , то есть
, то есть ![]() . В этом случае уравнение принимает вид:
. В этом случае уравнение принимает вид: ![]() . Значит, корнем уравнения является число
. Значит, корнем уравнения является число ![]() , что больше
, что больше ![]() . То есть значение
. То есть значение ![]() нам подходит.
нам подходит.
Исследуем теперь случай, когда ![]() . В этом случае обе части уравнения можно поделить на
. В этом случае обе части уравнения можно поделить на ![]() . В результате приходим к следующему уравнению:
. В результате приходим к следующему уравнению:
![]()
Пусть ![]() . Ветви соответствующей параболы направлены вверх, поэтому для того, чтобы выполнялось требуемое условие, эта парабола должна быть расположена относительно оси OX условно следующим образом:
. Ветви соответствующей параболы направлены вверх, поэтому для того, чтобы выполнялось требуемое условие, эта парабола должна быть расположена относительно оси OX условно следующим образом:
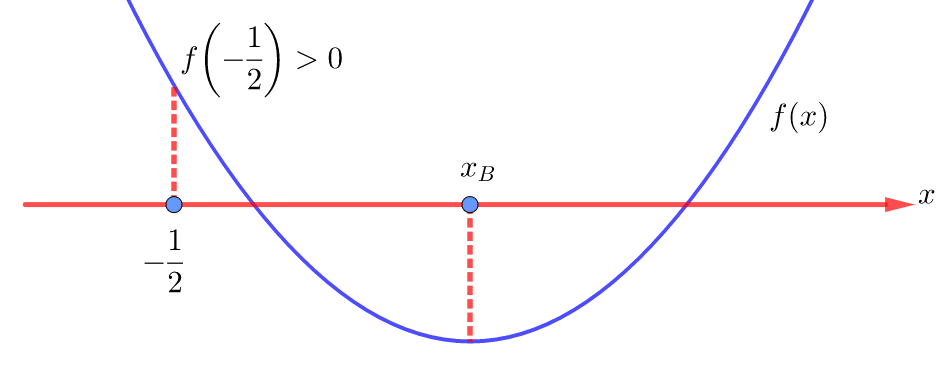
Из рисунка видно, что требуемое условие выполняется только в том случае, если соответствующий квадратный трёхчлен имеет корни (парабола пересекает ось OX или касается её), то есть его дискриминант неотрицателен, значение этого квадратного трёхчлена в точке ![]() положительно, и вершина соответствующей параболы, ветви которой направлены вверх, лежит правее точки
положительно, и вершина соответствующей параболы, ветви которой направлены вверх, лежит правее точки ![]() . То есть имеет место следующая система:
. То есть имеет место следующая система:
![Rendered by QuickLaTeX.com \[ \begin{cases} D\geqslant 0 \\ f\left(-\dfrac{1}{2}\right)>0 \\ x_B >-\dfrac{1}{2} \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-62d66ade0ff750ded93d05b9173e7ee3_l3.png)
Выражаем все величины через параметр ![]() и после всех упрощений получаем следующую систему:
и после всех упрощений получаем следующую систему:
![Rendered by QuickLaTeX.com \[ \begin{cases} \dfrac{a(5a-1)}{(a-1)^2}\geqslant 0 \\ \, \\ \dfrac{11a+1}{a-1}<0 \\ \, \\ \dfrac{3a+1}{a-1}<0 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8c88b7a23e2665cdce4d26ae96df9d8b_l3.png)
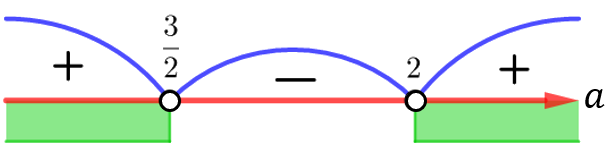
Каждое из неравенство системы решаем методом интервалов, а затем отбираем только те значения параметра ![]() , при которых выполняются все три неравенства системы.
, при которых выполняются все три неравенства системы.
Окончательный ответ к заданию имеет вид: ![]() .
.
|
Пример 4. Найдите все значения параметра |
Рассмотрим сперва случай, когда ![]() . В этом случае записанное уравнение принимает вид:
. В этом случае записанное уравнение принимает вид: ![]() . То есть корнем уравнения является число
. То есть корнем уравнения является число ![]() . Этот корень принадлежит промежутку
. Этот корень принадлежит промежутку ![]() , поэтому данный случай нам подходит.
, поэтому данный случай нам подходит.
Теперь рассмотрим случай, когда ![]() . В этом случае обе части уравнения можно поделить на
. В этом случае обе части уравнения можно поделить на ![]() . Тогда получаем следующее уравнение:
. Тогда получаем следующее уравнение:
![]()
Пусть ![]() . Ветви соответствующей параболы направлены вверх. Значит, для выполнения требуемого условия эта парабола должна быть расположена относительно оси OX условно следующим образом:
. Ветви соответствующей параболы направлены вверх. Значит, для выполнения требуемого условия эта парабола должна быть расположена относительно оси OX условно следующим образом:
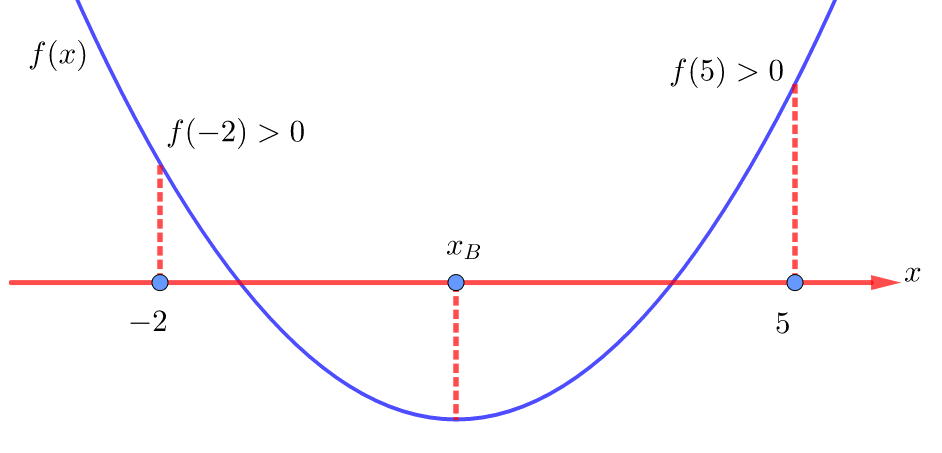
Из рисунка видно, что требуемое условие выполняется тогда и только тогда, когда корни уравнения с параметром существуют (парабола пересекает ось OX или касается её), то есть когда дискриминант соответствующего квадратного трёхчлена положителен или равен нулю, значения этого трёхчлена в точках ![]() и
и ![]() положительны, а вершина соответствующий параболы находится внутри промежутка
положительны, а вершина соответствующий параболы находится внутри промежутка ![]() . То есть имеет место следующая система:
. То есть имеет место следующая система:
![Rendered by QuickLaTeX.com \[ \begin{cases} D\geqslant 0 \\ f(-2)>0 \\ f(5)>0 \\ -2<x_B<5 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-484f344cf8d0bffd45a6e45fa03e7b27_l3.png)
Выражаем все величины через параметр ![]() и упрощаем получившиеся неравенства. В результате получаем следующую систему неравенств:
и упрощаем получившиеся неравенства. В результате получаем следующую систему неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} \dfrac{(2a-9)(2a-1)}{a^2}\geqslant 0 \\ \, \\ \dfrac{2a-1}{a}>0 \\ \, \\ \dfrac{15a+17}{a}>0 \\ \, \\ -2< \dfrac{2a-3}{2a} <5 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4bc436f73446c594cd89905d03508dad_l3.png)
Каждое из неравенств системы решается методом интервалов, после чего отбираются значения параметра ![]() , удовлетворяющие каждому из неравенств.
, удовлетворяющие каждому из неравенств.
В результате получаем окончательный ответ:
![]() .
.
Корни уравнения с параметром для самостоятельного решения
Решите следующие задания самостоятельно для самопроверки понимания изложенного в статье материала. Если при выполнении этих заданий у вас возникнут вопросы, задавайте их в комментариях, а также пишите в них свои попытки и варианты решений.
- Найдите все значения параметра
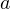 , при каждом из которых один из корней уравнения
, при каждом из которых один из корней уравнения 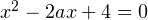 меньше 2, а другой больше 2.
меньше 2, а другой больше 2.
Ответ: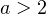 .
. - Найдите все значения параметра
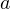 , при каждом из которых один из корней уравнения
, при каждом из которых один из корней уравнения 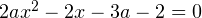 больше 1, а другой меньше 1.
больше 1, а другой меньше 1.
Ответ: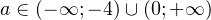 .
. - Найдите все значения параметра
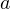 , при каждом из которых уравнение
, при каждом из которых уравнение 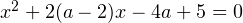 имеет два различных корня, каждый из которых больше -1.
имеет два различных корня, каждый из которых больше -1.
Ответ: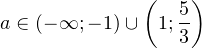 .
.
Материал подготовил репетитор по математике и физике в Москве Сергей Валерьевич

Спасибо. Получила много полезной информации.Все понятно и доступно.
В примере 4 описка в ответе: a не может быть равно 0. В этом месте должно быть а=0.5.
Нет, там всё правильно написано: a может быть равно 0 (первый абзац в решении), a = 0.5 не подходит, так как тогда получается один корень x = 2, который не входит в указанный в условии промежуток.