
В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.
Определение средней скорости
Средней скоростью движения ![]() тела называется отношение пути
тела называется отношение пути ![]() , пройденного телом, ко времени
, пройденного телом, ко времени ![]() , в течение которого двигалось тело:
, в течение которого двигалось тело:
![]()
Научимся ее находить на примере следующей задачи:
| Тело двигалось 3 мин. со скоростью 5 м/с, после чего 7 мин. двигалось со скоростью 3 м/с. Найти среднюю скорость движения тела. |
- Переведем все величины в Международную систему единиц СИ. В этой системе единицей измерения времени является секунда. Следовательно, тело двигалось на первом участке пути в течение
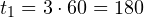 с, а на втором участке пути в течение
с, а на втором участке пути в течение 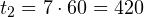 с.
с. - Найдем теперь полный путь, пройденный телом. На первом участке тело прошло
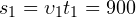 м пути. На втором участке пути тело прошло
м пути. На втором участке пути тело прошло 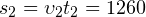 м пути. Следовательно, общий пройденный телом путь составляет
м пути. Следовательно, общий пройденный телом путь составляет 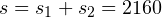 м.
м. - Общее время движения составляет
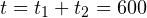 с. Следовательно, средняя скорость движения тела составляет:
с. Следовательно, средняя скорость движения тела составляет:
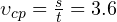 м/с.
м/с.
Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей ![]() и
и ![]() , которое равно:
, которое равно:
![]() м/с.
м/с.
Частные случаи нахождения средней скорости
1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью ![]() , а вторую половину пути — со скоростью
, а вторую половину пути — со скоростью ![]() . Требуется найти среднюю скорость движения тела.
. Требуется найти среднюю скорость движения тела.
- Пусть
 — общая длина пройденного пути. Тогда на первом участке пути тело двигалось в течение интервала времени
— общая длина пройденного пути. Тогда на первом участке пути тело двигалось в течение интервала времени 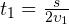 . Аналогично, на втором участке пути тело двигалось в течение интервала времени
. Аналогично, на втором участке пути тело двигалось в течение интервала времени 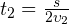 .
. - Тогда средняя скорость движения равна:
![Rendered by QuickLaTeX.com \[ \upsilon_{cp} = \frac{s}{t_1+t_2} = \frac{s}{\frac{s}{2\upsilon_1}+\frac{s}{2\upsilon_2}} = \frac{2\upsilon_1\upsilon_2}{\upsilon_1+\upsilon_2}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7360def65faa837f59240afaf124708c_l3.png)
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью ![]() в течение некоторого промежутка времени, а затем стало двигаться со скоростью
в течение некоторого промежутка времени, а затем стало двигаться со скоростью ![]() в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
- Пусть
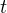 — общее время пути. Тогда путь, пройденный телом в течение первой половины времени движения, равен:
— общее время пути. Тогда путь, пройденный телом в течение первой половины времени движения, равен: 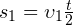 . Аналогично, путь, пройденный телом в течение второй половины времени движения, равен:
. Аналогично, путь, пройденный телом в течение второй половины времени движения, равен: 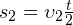 .
. - Тогда средняя скорость движения равна:
![]()
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей ![]() и
и ![]() на двух участках пути.
на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
| Тело двигалось |
Пройденный телом путь составляет: ![]() м. Можно найти также путь, который прошло тело за последние
м. Можно найти также путь, который прошло тело за последние ![]() с своего движения:
с своего движения: ![]() м. Тогда за первые
м. Тогда за первые ![]() с своего движения тело преодолело путь в
с своего движения тело преодолело путь в ![]() м. Следовательно, средняя скорость на этом участке пути составила:
м. Следовательно, средняя скорость на этом участке пути составила:
![]() м/с.
м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Репетитор по физике на Юго-Западной
Сергей Валерьевич

Добрый день. Подскажите, пожалуйста, почему среднюю скорость нельзя найти как среднее арифметическое скоростей?
Добрый день, потому что для нахождения средней скорости нужно пройденный путь разделить на время, затраченное на его прохождение. В общем случае это отношение не равно среднему арифметическому скоростей.
потому что такие случаи когда формула средней скорости и среднего арифметического совпадают являются частными случаями
Это следует из определения средней сеорости. Можнографически увидеть треугольник, если по абсциссе отложит время, по ординате путь.и мы знаем, что гипотинуза всегда меньше суммы катетов
Не понимаю, что вы имеете в виду. Да, гипотенуза меньше суммы катетов. И что это доказывает?
Как в последнем примере из отношения 40 на 4 получается 2.5?
Это s_1/t_1 = 40/16 =2.5 м/с. Исправлено, спасибо.
Средняя скорость-это отрезок пути с равномерным движением. Начальная скорость= конечной. Это: S/t, или (v+v):2.
Все расчёты на S,t,V,F,m,a надо делать, исходя из СРЕДНЕЙ скорости V ср.
Если S/tt=F/m — значит это движется «конкретное» тело-(машина, человек, яблоко..) V ср. падающего «яблока….»=4,9 м/с. а=4,9 м/сс. (9,8-это конечная скорость)
а что делать если известно 2 скорости одинаковое время и больше неизвестно ничего.
Это частный случай, когда средняя скорость находится как среднее арифметическое двух скоростей. В общем случае так делать нельзя.
при равноускоренном движении v ср=(v+V)/2, а при равномерном движении V нач.=V ср=V кон. V=(V+V)/2
откуда берется магическое число 2
вопрос поставлен верно! S/tt. S/t=V средняя. V ср./t=a. Обратно: a*t=V средняя. V cр.*t=att ……………………………………………………………..V конеч./2=V средней. V ср.=at. Vср(at)*2=V конечной. Или: V конечная=2at.
S=(0+2at)/2*t S=att. a=s/tt (а НЕ 2S/tt)
Ускорение «яблока…»= 4,9/1*1. а=4,9 м*сс. (9,8-это КОНЕЧНАЯ скорость,=2at)
Пожалуйста ответьте мне откуда берём эти цифры там з умножаем на 60 минут или секунд
Секунд, потому что переводим минуты в секунды
Скорость «at»- это СРЕДНЯЯ скорость! Конечная скорость есть 2at.
F/m-то-же «ускорение». Ньютон стремился уравнять S/tt и F/m, но из-за ошибки att/2 равенство не получалось…. Искать ускорение бессмысленно. А вот с помощью «а» можно найти S,t,F,m,V нач.,ср.,конеч.,n,КПД…. S/tt=F/m. Всё можно измерить, а F,n,КПД можно только рассчитать…
….камень весом 35 кг. перенесли на 25 м за 30 с. F=? Решение: 25/900=F/35. F=0,97 кг.м/с.
..машина m=1200 кг. прошла 250 м. за 20 с. КПД ДВС=16% (у ВСЕХ ! бензиновых ДВС) Считаем: n=? 250/400=F/1200. F-750 кг.м/с. Это 10 л.с. при 100% КПД. При 16% КПД n=62,5 л.с. (мотор может быть и 150 сил, но требуется только 62,5 силы…)
чему равна средняя скорость при только известной скрости и одинаковых растояний
Об этом рассказано в пункте №1 «Два одинаковых участка пути.»
Здравствуйте,а что если известна скорость половины пути и серость второй половины пути. Также известно,что половины пути равны. Заранее спасибо!❤️
А что делать если у тебя известно три скорости и больше н чего неизвестно
Что делать если известно только скорости
Об этом указано в первом пункте
Здравствуйте.помогите решить пожалуйста. Велосипедист прошел под путь 12 км/час. Весь путь прошло скоростью 8 км/час. Надо найти с какой скоростью прошел вторую половину пути
Здравствуйте.помогите решить пожалуйста. Велосипедист прошел под путь 12 км/час. Весь путь прошло скоростью 8 км/час. Надо найти с какой скоростью прошел вторую половину пути
vcp=2v1*v2/v1+v2
8=2*12*v2/12+v2
96+8v2=24v2
96=16v2
v2=6 км/ч
Aвтомобиль 2/3 пути проехал 6 м/с а остальную 9 м/с .Найти среднюю скорость.Помогите пожалуста
Что делать если известно что есть две скорости а путь и время неизвестны, то как найти ср. скорость?
Как найти среднюю скорость, если даны три скорости и больше ничего ?
Спасибо большое!!! Супер! Я сама преподаю математику в Казахстане. Успехов Вам
Как найти среднею скорость зная только скорость
скорость (просто) V и есть СРЕДНЯЯ скорость
А как найти среднюю скорость с тремя одинаковыми участками цепи?
По-моему среднюю скорость ВСЕГДА можно найти с помощью среднего арифметического. Просто надо выразить скорости так, чтобы с каждой ехали одинаковое количество времени. К примеру, если с одной V1 ехали t, а с другой V2 — 3t, то Vср=v1 + v2 + v2 + v2/ 4
Если требуется найти среднюю скорость за всё время, то да. Если же требуется найти среднюю скорость только за время, когда он двигался с отличной от нуля скоростью, то нет.
Здраствуйте,
А что если два движущихся тела и одно из них делает остановки?
Здравствуйте. Если даны только две скоростей, а как найти средную скорость? Заранее спасибо.
Здравствуйте! Подскажите, пожалуйста, чайнику. Есть ли формула вычисления скорости двух тел, движущихся в одном направлении, с разными скоростями, сцепленных друг с другом?