Предлагаю на этот раз устроить что-то вроде «доказательного марафона» по решению задач, которые предлагаются девятиклассникам в вариантах ГИА по математике. Связаны они с доказательством несложных, но в то же время очень полезных геометрических фактов. В статье намеренно не приведены подробные решения задач, лишь некоторые наброски и подсказки. Постарайтесь преодолеть эту марафонскую дистанцию самостоятельно, без ошибок и за один подход.
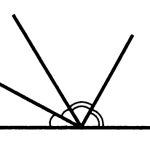
Задача 1. Докажите, что биссектрисы смежных углов перпендикулярны.
Доказательство: из рисунка видно, что α + α + β + β = 2α + 2β = 1800 (развернутый угол), следовательно, α + β = 900. Что и требовалось доказать.
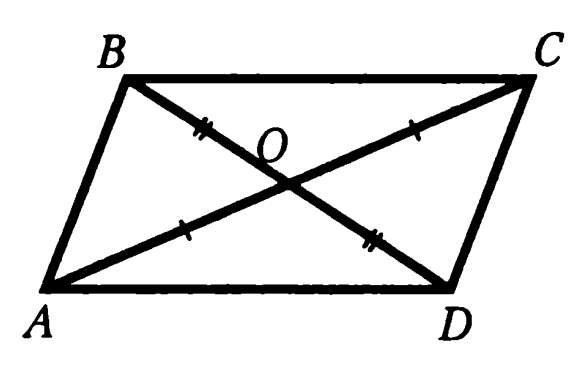
Задача 2. Два отрезка AC и BD пересекаются в точке O, которая является серединой каждого из них. Докажите равенство треугольников ACD и CAB.
Доказательство: боковые треугольники равны по двум сторонам и углу между ними (BO = OD — по условию, AO = OC — по условию, ∠DOC = ∠AOB — вертикальные), то есть ∠ACD = ∠CAB, а поскольку они являются накрест лежащими при прямых AB, CD и секущей AC, то AB параллельна DC. Аналогично доказываем параллельность прямых BC и AD. Итак, ABCD — параллелограмм по определению. BC = AD, AB = CD (в параллелограмме противоположные стороны равны), AC — общая для треугольников ACD и CAB, поэтому они равны по трем сторонам. Что и требовалось доказать.
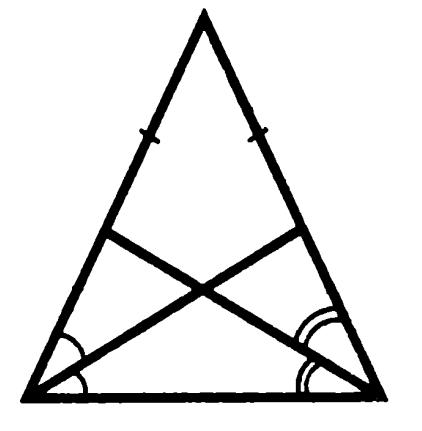
Задача 3. Докажите, что медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой угла, противолежащего основанию, а также перпендикулярна основанию.
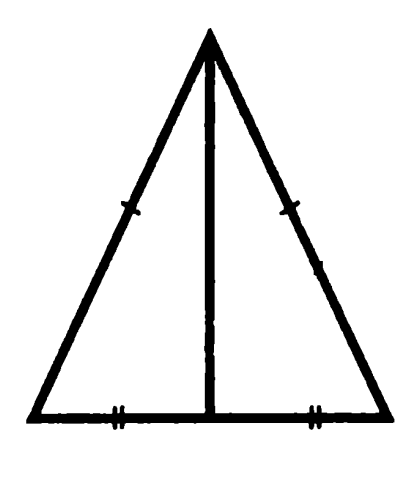
Углы, образованные медианой и основанием, назовем «нижними», медианой и боковыми сторонами — «верхними»
Доказательство: боковые треугольники на рисунке равны по трем сторонам, из чего следует равенство, во-первых, «верхних» углов (доказали, что биссектриса), во-вторых, «нижних» углов, в сумме как смежные дающих 1800, и равных поэтому по 900 каждый (доказали перпендикулярность). Что и требовалось доказать.
Задача 4. Докажите, что медианы, проведенные к боковым сторонам равнобедренного треугольника, равны.
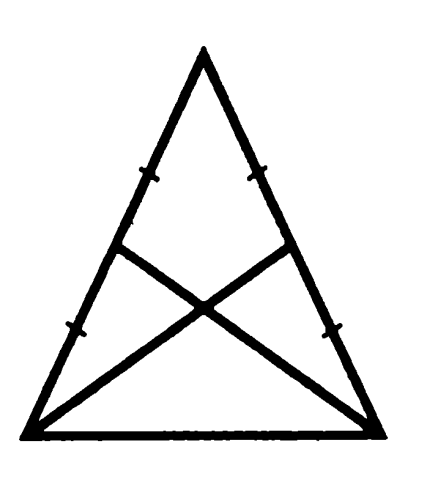
Треугольники, образованные медианами, основанием и нижними половинами боковых сторон исходного треугольника, назовем «нижними»
Доказательство: углы при основании равнобедренного треугольника равны, поэтому «нижние» треугольники равны по двум сторонам и углу между ними, из чего следует равенство проведенных медиан. Что и требовалось доказать.
Задача 5. Докажите, что биссектрисы, проведенные из вершин основания равнобедренного треугольника, равны.
Доказательство: «нижний» треугольник равнобедренный, что следует из равенства углов при его основании, «боковые» треугольники равны по стороне (равные из доказанного выше частички биссектрис) и двум углам (первые равны по условию, вторые как вертикальные), поэтому оставшиеся частички биссектрис также равны друг другу, а значит равны и сами биссектрисы целиком. Что и требовалось доказать.
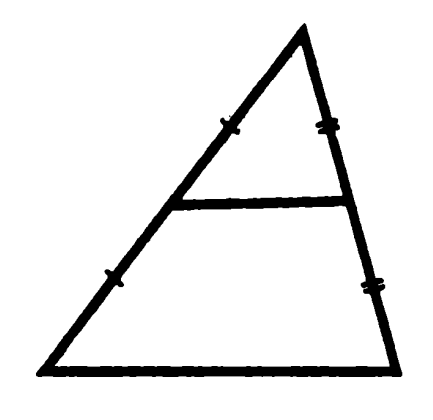
Задача 6. Докажите, что длина отрезка, соединяющего середины двух сторон треугольника, равна половине третьей стороны.
Доказательство: боковые стороны маленького и большого треугольника на рисунке относятся как 1 : 2, кроме того у них есть один общий угол, а значит они подобны по второму признаку с коэффициентом подобия 1 : 2, поэтому и основания относятся как 1 : 2. Что и требовалось доказать.
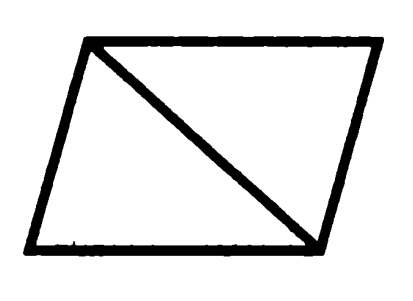
Задача 7. Докажите, что диагональ параллелограмма разбивает его на два равных треугольника.
Доказательство: противоположные стороны параллелограмма равны, диагональ является общей стороной для этих треугольников, поэтому они равны по трем сторонам. Что и требовалось доказать.
Задача 8. Докажите, что медиана, прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство: если вокруг данного прямоугольного треугольника описать окружность, то вписанный в эту окружность прямой угол треугольника будет описаться на полуокружность, поэтому гипотенуза будет диаметром этой окружности, а половинки гипотенузы и данная нам в задаче медиана — радиусами, итак, все они равны. Что и требовалось доказать.
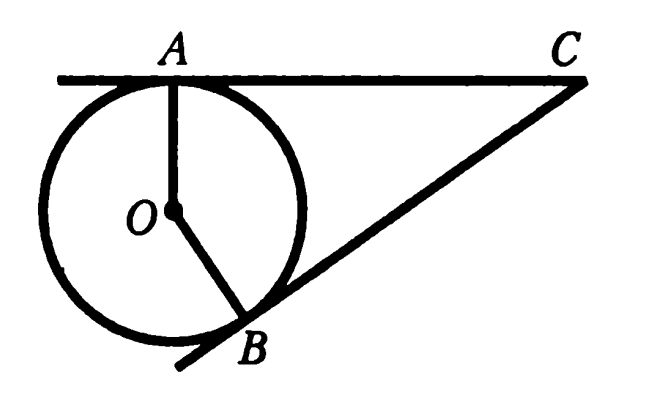
Задача 9. Докажите, что отрезки касательных, проведенных к окружности из одной точки, равны.
Доказательство: углы B и A прямые (радиусы окружности, проведенные в точку качания, перпендикулярны касательным), значит прямоугольные треугольники AOC и BOC равны по гипотенузе (общая для них воображаемая нами сторона OC) и катету (радиусы окружности OB = OA), а значит AC = CB. Что и требовалось доказать.
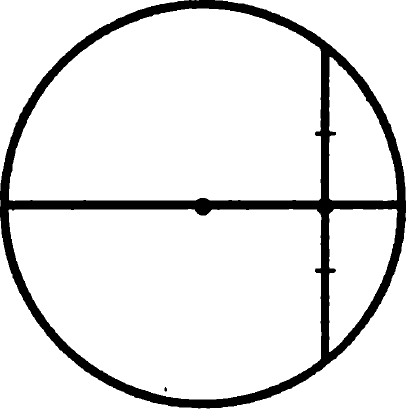
Задача 10. Докажите, что диаметр, проходящий через середину хорды окружности, перпендикулярен ей.
Доказательство: в равнобедренном треугольнике, образованном точками пересечения хорды с окружностью и центром этой окружности, изображенная медиана будет являться высотой, а значит диаметр, содержащий в себе эту высоту, перпендикулярен хорде. Что и требовалось доказать.
Задача 11. Докажите, что если две окружности имеют общую хорду, то прямая, проходящая через центр этих окружностей, перпендикулярна данной хорде.

Мысленно соединяем вместе все отмеченные на рисунке точки, точку пересечения горизонтали и вертикали назовем H
Доказательство: треугольники O1AO2 и O1BO2 равны по трем сторонам, следовательно, ∠HO2A = ∠HO2B, тогда треугольники HAO2 и HBO2 равны по двум сторонам и углу между ними, значит ∠AHO2 = ∠BHO2, а в сумме два равных угла могут давать 1800 только в том случае, если каждый из них равен по 900. Что и требовалось доказать.
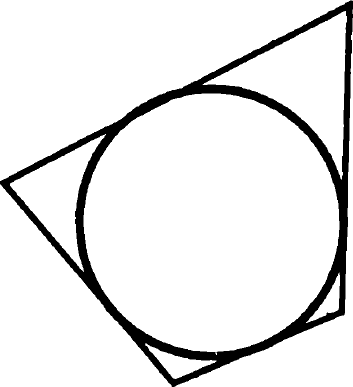
Задача 12. Докажите, что если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.
Доказательство: используем теорему об отрезках касательных (задача 9). ВК = ВР, СР = СН, DX = DL и АТ = АК. Суммируем стороны АВ и CD: AB + CD = (AM + MB) + (DX + XC) = AL + BE + DL + CE = (AL + LD) + (BE + EC) = AD + BC. Что и требовалось доказать.
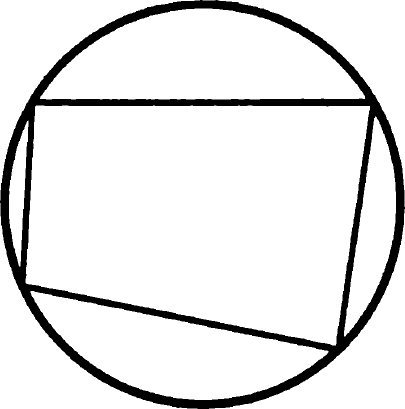
Задача 13. Докажите, что если около четырехугольника можно описать окружность, то суммы его противолежащих углов равны.
Доказательство: по теореме о вписанном угле сумма противолежащих углов этого четырехугольника равна 1800, поскольку вместе они опираются на полную окружность, градусная мера которой 3600. Что и требовалось доказать.
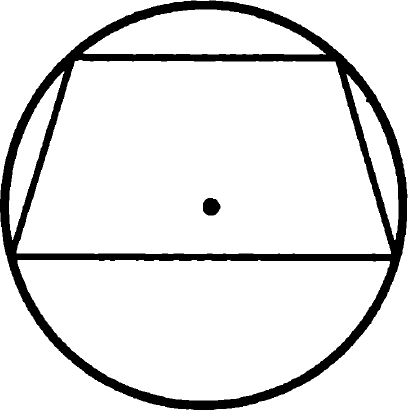
Задача 14. Докажите, что если около трапеции можно описать окружность, то трапеция равнобедренная.
Доказательство: сумма противолежащих углов четырехугольника, вписанного в окружность, равна α + β = 1800 (см. задачу 13), сумма углов при боковой стороне трапеции также равна α + γ = 1800 (эти углы являются односторонними при параллельных основаниях и секущей боковой стороне), из сравнения этих формул получаем, что β = γ, то есть углы при основании такой трапеции равны, и она действительно равнобедренная. Что и требовалось доказать.
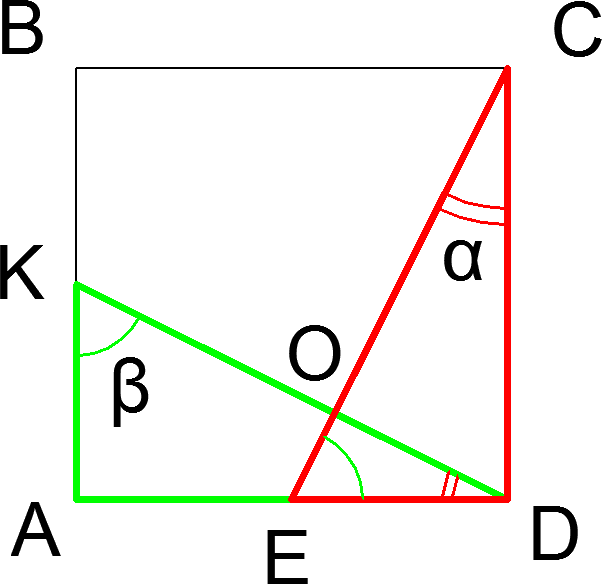
Задача 15. В квадрате ABCD точки К и Е — середины сторон АВ и AD соответственно. Доказать, что КD перпендикулярна CE.
Доказательство. Прямоугольные треугольники AKD и ECD равны по двум катетам, поэтому равны и все их элементы. Пусть ![]()
![]()
Сумма углов в треугольнике равна ![]() Тогда, например, для треугольника AKD имеем
Тогда, например, для треугольника AKD имеем ![]() а значит
а значит ![]() Для треугольника EOD имеем
Для треугольника EOD имеем ![]()
![]() то есть
то есть ![]() а значит
а значит ![]() Что и доказывает перпендикулярность KD и CE.
Что и доказывает перпендикулярность KD и CE.
Доказанные геометрические факты очень важны, их знание будет вам хорошим подспорьем в решении более сложных задач по геометрии, в первую очередь заданий C4 из вариантов ЕГЭ по математике. Изложенные здесь пояснения эталонными решениями, которые нужно приводить на экзамене, конечно, не являются. Это лишь указатели, используя которые, читатель сможет найти решение самостоятельно.
В любом случае умение решать задачи по геометрии является неотъемлемым условием получения высоких баллов на ЕГЭ и ГИА по математике, что будет гарантией поступления во многие престижные вузы. Успехов вам в подготовке к ГИА и ЕГЭ, талантливых наставников и удачи на экзамене! Ваш репетитор по геометрии Сергей Валерьевич.
Понравилась статья? Возможно, это будет вам интересно:


А где треугольник в круге