В задании 18 профильного уровня ЕГЭ по математике школьникам предлагается решить задачу с параметром. Такие задания надо уметь решать. К сожалению, решению именно этого класса задач в школе уделяется очень мало внимания. В данной статье репетитором по математике представлен подробный разбор двух типов заданий 18 профильного ЕГЭ по математике, которые были предложены на экзамене в 2016 году. Имеется видеоразбор решений.
| Найдите значения параметра имеет ровно три различных решения. |
Для тех, кто не хочет читать, доступен видеоразбор:
Чтобы корни существовали, правая часть уравнения должна быть положительной или равно нулю. В этом случае получаем систему:
![Rendered by QuickLaTeX.com \[ \begin{cases} 15x^2+6ax+9 = (x^2+ax+3)^2 \\ x^2+ax+3\geqslant 0 \end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-6f2852af50ab54d24a3cda7cf8dde403_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases} x^2(9-x^2-2ax-a^2) = 0 \\ x^2+ax+3\geqslant 0 \end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f9ca4e950a9e8b32de06fe4fe7909510_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases} x^2(9-(x+a)^2) = 0 \\ x^2+ax+3\geqslant 0 \end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-533e5fe59b47f06aa362a7cf39d45550_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases} x^2(3-x-a)(3+x+a) = 0 \\ x^2+ax+3\geqslant 0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-68ef24b955e6d8ca831b1fce05ad6b69_l3.png)
Находим корни первого уравнения:
![Rendered by QuickLaTeX.com \[ \begin{cases} \left[\begin{array}{l} x_1 = 0 \\ x_2 = -a-3 \\ x_3 = 3-a \end{array} \\ x^2+ax+3\geqslant 0 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-287e2fc76d6807ba49024738ecba88b8_l3.png)
Первый корень удовлетворяет неравенству. Ищем такие значения ![]() , при которых второй и третий корни не совпадают, не равны нулю и удовлетворяют неравенству:
, при которых второй и третий корни не совпадают, не равны нулю и удовлетворяют неравенству:
![Rendered by QuickLaTeX.com \[ \begin{cases} -a-3 \ne 3-a \\ 3-a \ne 0 \\ -a-3 \ne 0 \\ (3-a)^2+a(3-a)+3\geqslant 0 \\ (-a-3)^2+a(-a-3)+3\geqslant 0 \end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5d04c8cac5b2a1abac89f430d6053019_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases} a \ne 3 \\ a \ne -3\\ 12-3a\geqslant 0 \\ 3a+12\geqslant 0 \end{cases}\Leftrightarrow \begin{cases} a \ne 3 \\ a \ne -3\\ a\leqslant 4 \\ a\geqslant -4 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2f952900e53233867c6654eda1d82fe3_l3.png)
Итак, ответ ![]() .
.
| Найдите все значения a, при каждом из которых уравнение
имеет единственный корень. |
Для тех, кто не хочет читать, доступен видеоразбор:
Преобразуем выражение:
![]()
Раскроем скобки и приведём подобные слагаемые, после чего получим:
![Rendered by QuickLaTeX.com \[ \frac{x^2-2ax-x+2a^2+2a-2}{(x+2)(x-a)} = 0\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f7594469d88c07f72b3e5e4c65b8eb2e_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{x^2-2ax+a^2-x+a+\frac{1}{4}+a^2+a+\frac{1}{4}-\frac{5}{2}}{(x+2)(x-a)} = 0\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-64013e42bee2366dccf319c2ce488572_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{(x-a)^2-(x-a)+\frac{1}{4}+a^2+a+\frac{1}{4}-\frac{5}{2}}{(x+2)(x-a)} = 0\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-70d13b3d15fa9c509ac1a146f169a438_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{\left(x-a-\frac{1}{2}\right)^2+\left(a+\frac{1}{2}\right)^2-\frac{5}{2}}{(x+2)(x-a)} = 0. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-febd5ba7cbf27271a22d5e139de201c9_l3.png)
Введём замену: ![]() , получаем следующее выражение:
, получаем следующее выражение:
![Rendered by QuickLaTeX.com \[ \frac{\left(y-\frac{1}{2}\right)^2+\left(a+\frac{1}{2}\right)^2-\frac{5}{2}}{y(y+a+2)} = 0. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8711b5069bbf3bc5f43bf367cff8080a_l3.png)
Теперь задание сводится к тому, чтобы найти такие ![]() , при которых полученное уравнение имеет единственное решение
, при которых полученное уравнение имеет единственное решение ![]() , отличное от
, отличное от ![]() и
и ![]() .
.
Геометрическим местом точек, удовлетворяющих условию
![Rendered by QuickLaTeX.com \[ \left(y-\frac{1}{2}\right)^2+\left(a+\frac{1}{2}\right)^2=\frac{5}{2}, \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f4dfa4da27958a374072f0a5176f7e89_l3.png)
является окружность в плоскости aOy с центом в точке ![]() и радиусом
и радиусом ![]() . Путём подстановки в уравнение можно убедиться, что этой окружности принадлежат точки
. Путём подстановки в уравнение можно убедиться, что этой окружности принадлежат точки ![]() ,
, ![]() и
и ![]() .
.
Из этой окружности нужно удалить точки, удовлетворяющие условию ![]() и
и ![]() . При этом возможны только следующие значения
. При этом возможны только следующие значения ![]() , при которых
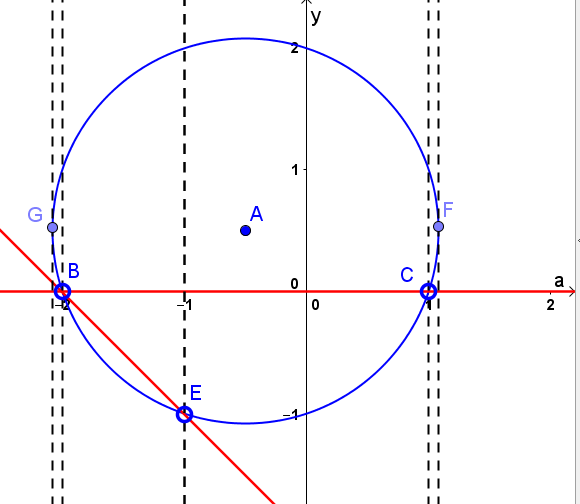
, при которых ![]() будет единственным (пунктирные линии на рисунке):
будет единственным (пунктирные линии на рисунке):
Ищем абсциссы точек F, C, E, B, G:
- абсцисса точки F равна
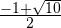 ;
; - абсцисса точки C равна 1;
- абсцисса точки E равна -1;
- абсцисса точки B равна -2;
- абсцисса точки G равна
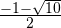 .
.
Репетитор для подготовки в ЕГЭ по математике, Сергей Валерьевич

Здравствуйте, Сергей! Я рассмотрела уже несколько решений подобных заданий и поняла, что все они очень разные и по разному решаются. Скажите, можно ли вообще научиться их решать? И если да, то есть ли какая-то методика? или сайт? или книга? Заранее благодарю за ответ.
Здравствуйте, Вероника. Универсальной методики, которая бы подходила всем, конечно, нет. Но если задаться целью и решать такие задачи каждый день по 1-2 штуки, то научиться их решать можно. А книг по этой тематике с разбором самых разнообразных примеров очень много. Начать можно с классического пособия Ткачука «Математика абитуриенту», к примеру.
Вероника, чтобы «научиться» решать такие задачи, есть 2 пути (ИМХО).
1. (малоэффективный, но ведущий к интеллектуальному росту) Каждый день решать по две задачи из Ткачука (варианты: Потапов-Олехник-Нестеренко, … …)
2. Получить полноценное высшее техническое образование, проскочив ЕГЭ, впоследствии стать преподавателем университета с продвинутой математикой (для гонора) и репетитором (для хлеба). Тогда никто не сможет Вас обмануть, делая вид, что задача замышлялась в таком виде. как была подана. С точки зрения школьника «№18» — это трудная задача с параметром. С точки зрения «повара» кухни, где готовилось блюдо — скучное нагромождение кусков гипербол и частей прямых в плоскости (x,a). То решение, которое (почти) верно изложено в приведённом видео, есть перевод простой и всем (репетиторам) понятной образной геометрической логики на неповоротливый русский математический подъязык.
По-русски: тупая задача.
Дело не в том, что задача тупая. Дело в том, что весь ЕГЭ такой. Но сдавать его всё равно надо. Вопрос в том, как подготовиться. В школе — не вариант. Научат решать только самые простые задачи. Курсы — сомнительный вариант. Тот же учитель у доски, тот же класс, те же проблемы. Можно пробовать самостоятельно. Способ очень хороший, но слишком долгий. Вот в чём корень зла. Времени всегда не хватает. Да и как готовиться? Решать задачи в случайном порядке в надежде извлечь из этого хаоса что-то рациональное? Это ж годы уйдут! А вот репетитор знает, как нужно готовить. Если он профессионал, конечно. Как бы пафосно это ни звучало, репетитор — это тот самый проводник, который ведёт ученика сквозь дебри разрозненных фактов, теорем, доказательство, задач с параметрами, тригонометрических уравнений и т.д., и т.д. А на выходе — знания, умения и навыки, необходимые для сдачи экзамена. Просто не всегда есть возможность заниматься с репетитором. Но это проблема очень многих в нашей стране. Тут уже только на себя приходится надеяться. Нужно пытаться подготовиться самостоятельно.
Здравствуйте. Начал рассматривать первый пример и задался вопросом: «Почему правая часть должна быть больше либо равна нулю???» Правая часть может принимать какие угодно значения, а вот подкоренное выражение в левой части должно быть больше либо равно нулю
Здравствуйте. Правая часть, поскольку она равна левой, в обязательном порядке должна быть больше либо равна нулю.
Я бы написал левая часть больше или равна нулю и правая… Почему так нельзя?
Потому что это дополнительное неравенство в системе, которое нужно решать. Ошибки не будет, если так написать. Результат решения будет тем же самым. Но это лишняя бессмысленная работа. Любой более-менее знающий математику специалист скажет Вам, что это математически неграмотно.
разве уравнение вида √а=b не имеет ограничений a≥0 b≥0 ?
Достаточно только одного ограничения b≥0. Потому что в этом случае a=b^2, и условие a≥0 следует из этого автоматически.
Было (x+2)(x-a). КАК после замены получилось у(у+а+2)????
Замена была y=x-a. Ну и подставьте это в выражение y(y+a+2). Получите (x+2)(x-a).
Почему нет проверки на ОДЗ во втором примере? x=-2 — посторонний корень.
Подставьте вместо a значение -2 в исходное уравнение и увидите, что это не постороннее решение.
Почему в конце х не должен быть = 0, т. е. — 3-a не равно 0 и 3-a не равно нулю, если подставить вместо х 0, то решение, вроде, получается, например, вначале корень из 9=3, а позже 0+0+3 больше 0???
Потому что один нулевой корень уже есть, остальные должны быть другими.
здравствуйте. я посмотрела первое видео. и не могу кое-что понять. два момента. почему у вас на времени 1.27 в правой системе получилось -9х^2? там же получается после переноса влево, что из 15 вычитаем 6. а 15 положительное… почему минус?
и второй момент. на времени 2.16, где раскладывали разность квадратов, не пониманию, почему в скобке (3-х-а) вы нашли, что х= -а-3… просто. если эту скобку к 0 приравнять, то х=3-а… объясните, пожалуйста.
из-за того, что у вас знак неправильно написан, (там должен быть +, а не -. и тогда скобка немного по-другому раскроется.) далее решение для тех, кто действительно вдумывается, а не просто палит в экран, не особо связное.
Этот вопрос уже обсуждался. Посмотрите на первый комментарий к видео на канале. А х=-а-3 получается из скобки (3+x+a).
Смотрю разбор первой задачи. Когда вы выносите х², в скобках у вас остаётся 9 со знаком плюс, но изначально оно было отрицательным. Привожу строки уравнения:
1) -х⁴ — 2ах² — 9х² — а²х² = 0
2) х² (9 — х² — 2ах — а²)=0
Да, это опечатка была, но она не повлияла на ход решения.
не поняла, там же явная ошбка, почему у вас получилось — 9? Когда 9 со знаком + идёт
всё, разобралась, опечатка
у вас неправильно решено первое в конце,второе неравенство в системе не такое выходит,пересчитайте
ой,все правильно,извините)
какой метод сложнее аналитический или графоаналитический?