Построение графика квадратичной функции всегда было проблемой для многих школьников. Проблема в том, что на уроках в школе этому важнейшему материалу зачастую уделяют не достаточно внимания. В результате, когда появляется необходимость, ученику очень трудно отыскать в школьном учебнике или интернете чёткий алгоритм построения графика квадратичной функции (параболы), а вместо этого приходится по крупицам выискивать необходимую информацию из множества различных источников. Решим эту проблему раз и навсегда! В данной статье репетитором по математике и физике представлен алгоритм построения параболы.
| Квадратичной называется функция вида:
|
Алгоритм построения графика функции y=ax²+bx+c
Данный алгоритм продемонстрируем на примере построения графика квадратичной функции ![]() . В этом случае:
. В этом случае: ![]() ,
, ![]() и
и ![]() .
.
1. Определим, куда направлены ветви соответствующей параболы. Если ![]() , то ветви параболы направлены вверх, если
, то ветви параболы направлены вверх, если ![]() , то ветви параболы направлены вниз.
, то ветви параболы направлены вниз.
В нашем примере ![]() . Следовательно, ветви параболы направлены вниз.
. Следовательно, ветви параболы направлены вниз.
2. Найдем координаты вершины параболы. Абсцисса вершины параболы определяется по формуле:
![]()
Ордината вершины параболы ![]() определяется путем подстановки
определяется путем подстановки ![]() в уравнение квадратичной функции и вычисления соответствующего значения.
в уравнение квадратичной функции и вычисления соответствующего значения.
В нашем случае абсцисса ![]() вершины параболы равна:
вершины параболы равна:
![]()
Тогда ордината ![]() вершины параболы равна:
вершины параболы равна:
![Rendered by QuickLaTeX.com \[ y_0 = -2\cdot \left(\frac{1}{2}\right)^2+2\cdot \frac{1}{2} + 4 = \frac{9}{2}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-6d250574287aa0ce5cef93877b14e270_l3.png)
3. Определим еще несколько точек вблизи вершины, принадлежащих параболе. Удобнее всего оформить эти точки в виде таблицы.
В нашем случае получаем следующую таблицу значений:
| -2 | -1 | 0 | 1 | 2 | 3 | |
| -8 | 0 | 4 | 4 | 0 | -8 |
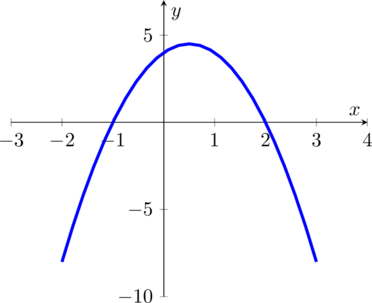
4. Отметить полученные точки и вершину параболы на координатной плоскости и соединить их плавной линией. В результате получится требуемый график квадратичной функции.
В нашем случае получается следующая парабола:
Репетитор по математике и физике
Сергей Валерьевич
| Квадрат — зародыш всех возможностей. (Казимир Малевич) |

Очень полезная инфа, спасибо . Готовлюсь к экзаменам , очень помогли..
Выпускной класс, это сложно(
Спасибо за полезную информацию очень полезно готовлюсь к ОГЕ
оч полезный сайт помог на откром уроке
Спасибо , бро
Не совсем понятно как строится таблица , x понятно , а откуда берутся значения y ?
согласен
А откуда взяты данные таблицы?
Берём произвольный набор значений x, для каждого по записанной формуле считаем y
Спасибо большое за алгоритм!