 Поступить в СУНЦ МГУ хотят многие школьники со всех уголков России, но удаётся это только лучшим из лучших. Для поступления в школу-интернат им. А.Н. Колмогорова нужно успешно сдать вступительные экзамены. Попробуйте решить предложенные в статье задания из типового варианта вступительного экзамена в СУНЦ МГУ по математике для поступающих в 10 класс (физико-математический профиль) и узнайте, готовы ли вы к поступлению в эту школу. Все задания снабжены подробными комментариями и решениями от репетитора по математике.
Поступить в СУНЦ МГУ хотят многие школьники со всех уголков России, но удаётся это только лучшим из лучших. Для поступления в школу-интернат им. А.Н. Колмогорова нужно успешно сдать вступительные экзамены. Попробуйте решить предложенные в статье задания из типового варианта вступительного экзамена в СУНЦ МГУ по математике для поступающих в 10 класс (физико-математический профиль) и узнайте, готовы ли вы к поступлению в эту школу. Все задания снабжены подробными комментариями и решениями от репетитора по математике.
| 1. Велосипедисту надо было проехать расстояние в 30 км. Выехав на 3 минуты позже назначенного срока, он ехал со скоростью на 1 км/час большей, чем планировал, и приехал на место вовремя. С какой скоростью ехал велосипедист? |
Пусть запланированная скорость велосипедиста равна ![]() километр в минуту. Тогда с запланированной скоростью он должен был проехать 30 км пути за
километр в минуту. Тогда с запланированной скоростью он должен был проехать 30 км пути за ![]() минут. Его фактическая скорость равна
минут. Его фактическая скорость равна ![]() километр в минуту. Тогда фактически он проехал расстояние 30 км за
километр в минуту. Тогда фактически он проехал расстояние 30 км за ![]() минут. Известно, что велосипедист реально выехал на 3 минуты позже запланированного срока, то есть двигался на 3 минуты меньше, чем было запланировано изначально. Поэтому имеет место уравнение:
минут. Известно, что велосипедист реально выехал на 3 минуты позже запланированного срока, то есть двигался на 3 минуты меньше, чем было запланировано изначально. Поэтому имеет место уравнение:
![]()
Следовательно, реальная скорость велосипедиста была равна ![]() километров в минуту.
километров в минуту.
| 2. Решить уравнение |
Для ![]() получаем
получаем ![]() , откуда находим
, откуда находим ![]() и
и ![]() .
.
Для ![]() получаем
получаем ![]() , откуда получаем
, откуда получаем ![]() . Второй корень этого уравнения
. Второй корень этого уравнения ![]() .
.
| 3. В геометрической прогрессии |
Из условия известно, что имеет место равенство:
![]()
Ни одно из записанных чисел не равно нулю, поскольку они являются членами геометрической прогрессии. Значит, можно поделить обе части получившегося равенства на выражение ![]() . Тогда получаем следующее выражение:
. Тогда получаем следующее выражение:
![]()
Но любая дробь в этом произведении равна ![]() — знаменателю этой прогрессии. Всего в этом произведении стоит ровно 1008 дробей. Тогда имеет место равенство:
— знаменателю этой прогрессии. Всего в этом произведении стоит ровно 1008 дробей. Тогда имеет место равенство:
![]()
| 4. В остроугольном треугольнике |
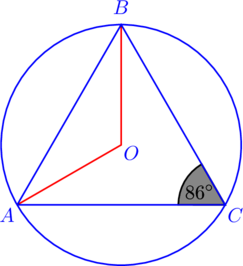
Вписанный угол ![]() опирается на дугу
опирается на дугу ![]() , поэтому градусная мера дуги
, поэтому градусная мера дуги ![]() равна
равна ![]() . Угол
. Угол ![]() является центральным и опирается на ту же дугу, поэтому
является центральным и опирается на ту же дугу, поэтому ![]() .
. ![]() , так как центр описанной около треугольника окружности равноудалён от его вершин. Поэтому треугольник
, так как центр описанной около треугольника окружности равноудалён от его вершин. Поэтому треугольник ![]() — равнобедренный.
— равнобедренный.
Значит ![]() .
.
| 5. Корни квадратного уравнения |
Пусть ![]() и
и ![]() — целочисленные корни уравнения, причём пусть для определенности
— целочисленные корни уравнения, причём пусть для определенности ![]() . Тогда из условия задачи и из теоремы Виета следует следующая система:
. Тогда из условия задачи и из теоремы Виета следует следующая система:
![Rendered by QuickLaTeX.com \[ \begin{cases} a+b = -p \\ ab = q \\ p+q = 112 \end{cases}\Leftrightarrow a+b-ab = -112. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3905d74a58f27791939b073828da59ef_l3.png)
Заметим сразу, что ![]() , поэтому последнее уравнение можно преобразовать к виду:
, поэтому последнее уравнение можно преобразовать к виду:
![]()
Последнее уравнение решается в целых числах при следующих ![]() :
:
![]()
В этих случаях соответствующие значения ![]() и
и ![]() равны:
равны:
![]()
Репетитор по математике и физике, осуществляющий подготовку к поступлению в СУНЦ МГУ, Сергей Валерьевич
