 В данной статье представлен разбор примера варианта вступительного испытания по математике в РЭУ им. Г.В. Плеханова от профессионального репетитора, занимающегося подготовкой абитуриентов к поступлению в этот университет. Все решения снабжены подробными комментариями и пояснениями, так что при желании каждый сможет самостоятельно разобраться со всеми заданиями.
В данной статье представлен разбор примера варианта вступительного испытания по математике в РЭУ им. Г.В. Плеханова от профессионального репетитора, занимающегося подготовкой абитуриентов к поступлению в этот университет. Все решения снабжены подробными комментариями и пояснениями, так что при желании каждый сможет самостоятельно разобраться со всеми заданиями.
Разбор варианта вступительного экзамена по математике в РЭУ им. Г.В. Плеханова
| 1. Вычислить
Варианты ответов: |
Вычислим значение, используя стандартные правила преобразования выражений, содержащих радикалы:
![]()
| 2. Корнем какого уравнения является число 2?
Далее идут варианты ответов с длинными уравнениями, которые я не буду здесь переписывать. |
Правильный ответ в):
![]()
поскольку из предложенных вариантов только для данного уравнения при подстановке вместо ![]() везде числа 2, оно обращается в верное равенство.
везде числа 2, оно обращается в верное равенство.
| 3. 25% учащихся 11 класса учатся только на отлично, а 50% учится только на хорошо. Число учащихся, имеющих удовлетворительные результаты, в 3 раза больше числа неуспевающих учеников. Сколько учеников в классе, если не успевают только 2 ученика? |
Приходится предположить, что в классе нет учеников, которые учатся на отлично и хорошо, иначе задача не имеет решения. Поскольку неуспевающих двое, то число учеников, которые имеют удовлетворительные результаты, равно 6. Пусть всего учеников в классе ![]() . Тогда число учащихся, которые учатся только на отлично, равно, очевидно,
. Тогда число учащихся, которые учатся только на отлично, равно, очевидно, ![]() . А число учащихся, которые учатся только на хорошо, соответственно,
. А число учащихся, которые учатся только на хорошо, соответственно, ![]() . Тогда имеет место равенство:
. Тогда имеет место равенство:
![]()
| 4. Решить уравнение
|
Введём замену ![]() и рассмотрим функцию
и рассмотрим функцию
![]()
Данная функция является возрастающей, так как равна сумме двух возрастающих функций. Это значит, что если эта функция принимает значение 7, то в при единственном значении ![]() . Это значение легко угадать:
. Это значение легко угадать: ![]() . То есть
. То есть ![]() , откуда получаем, что
, откуда получаем, что ![]() .
.
| 5. Решите неравенство
|
Переносим все члены в левую сторону неравенства и приводим всё к общему знаменателю:
![]()
Раскрываем скобки в числителе и приводим подобные слагаемые:
![]()
Воспользуемся в числителе формулой сокращённого умножения «квадрат разности»:
![]()
Теперь видно, что полученная дробь равна нулю при ![]() , а отрицательна она может быть только при отрицательном знаменателе, то есть при
, а отрицательна она может быть только при отрицательном знаменателе, то есть при ![]() , ибо в числителе выражение стоит в квадрате. Итак, окончательный ответ:
, ибо в числителе выражение стоит в квадрате. Итак, окончательный ответ: ![]() .
.
| 6. Боковое ребро правильной четырёхугольной пирамиды длиной 2 наклонено к плоскости основания под углом 30º. Найти объём пирамиды. |
1. В прямоугольном треугольнике AFE против угла A в 30º лежит катет EF, который равен половине гипотенузы AE. То есть ![]() . Высоту пирамиды нашли. Из того же прямоугольного треугольника по теореме Пифагора находим теперь
. Высоту пирамиды нашли. Из того же прямоугольного треугольника по теореме Пифагора находим теперь ![]() .
.
2. В основании правильной четырёхугольной пирамиды лежит квадрат ABCD. Ищем его сторону. ![]() . Записываем теорему Пифагора для прямоугольного треугольника ACD:
. Записываем теорему Пифагора для прямоугольного треугольника ACD: ![]() , где
, где ![]() — сторона квадрата. Значит,
— сторона квадрата. Значит, ![]() . Это есть площадь основания пирамиды.
. Это есть площадь основания пирамиды.
3. Объём пирамиды равен одной трети от произведения площади её основания на высоту. Значит, искомый объём равен 2.
| 7. Решить уравнение
|
Область допустимых значений данного уравнения определяется следующей системой неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} 2+5x-3x^2\geqslant 0 \\ x^2+x-6\geqslant 0 \\ x-1>0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ebe1f01393deed743ea90ea2dd1bd909_l3.png)
Решая эту систему. Первые два неравенства легко решаются методом интервалов. Последнее неравенство решается автоматически:
![Rendered by QuickLaTeX.com \[ \begin{cases} -\frac{1}{3}\leqslant a\leqslant 2 \\ a\in(-\mathcal{1};-3]\cup[2;+\mathcal{1}) \\ x>1. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-edf656ffcbcd06a8c1992d65d38ca128_l3.png)
В результате получаем, что в область допустимых значений входит одно единственной число ![]() . Прямой подстановкой убеждаемся, что это корень данного уравнения.
. Прямой подстановкой убеждаемся, что это корень данного уравнения.
| 8. Решить неравенство
|
Пусть ![]() . При этом сразу замечаем, что
. При этом сразу замечаем, что ![]() . Действительно, минимальное значение выражение
. Действительно, минимальное значение выражение ![]() принимает при
принимает при ![]() . Это минимальное значение равно 5. При всех остальных значениях
. Это минимальное значение равно 5. При всех остальных значениях ![]() значение выражения будет больше 5.
значение выражения будет больше 5.
С учётом этой замены неравенство можно переписать в следующем виде:
![]()
Начнём с того, что значения ![]() удовлетворяют этому неравенству. При всех остальных
удовлетворяют этому неравенству. При всех остальных ![]() выражением
выражением ![]() положительно. Значит, для
положительно. Значит, для ![]() мы может разделить обе части последнего неравенства на это выражение, не меняя при этом знак неравенства:
мы может разделить обе части последнего неравенства на это выражение, не меняя при этом знак неравенства:
(1) ![]()
Преобразуем полученное слева выражение при ![]() :
:
![]()
![]()
Определим, какие значения может принимать полученное выражение при ![]() :
:
![]()
![]()
Итак, получили:
![]()
Но, как мы выяснили раньше, ![]() , поэтому неравенство (1) не выполняется ни при каких
, поэтому неравенство (1) не выполняется ни при каких ![]() .
.
Итак, получается, что исходное неравенство выполняется только при ![]() .
.
| 9. В треугольнике ABC сторона AB = 1, сторона |
Для треугольника ACO имеем:
(2) ![]()
Для треугольника ABC имеем:
(3) ![]()
Из уравнения (2) получаем:
![]()
Подставляем этот результат в уравнение (3) и получаем:
![]()
Для нахождения стороны AC используем теперь теорему косинусов:
![]()
![Rendered by QuickLaTeX.com \[ =\sqrt{3-2\cdot\sqrt{2}\cdot\frac{\sqrt{2}}{2}} = 1. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-af68049ad2ec1f0dcab2d1d9bc017f98_l3.png)
Примечание. Параллельно, кстати, получилось, что треугольник ABC — равнобедренный и прямоугольный с прямым углом A. Но для изложенного решения это не потребовалось.
| 10. Найти все значения больше 1, а другой меньше 1. |
Заметим сразу, что ![]() нам не подходит, ибо в этом случае мы получаем линейное уравнение относительно
нам не подходит, ибо в этом случае мы получаем линейное уравнение относительно ![]() , которое не может иметь ровно двух корней.
, которое не может иметь ровно двух корней.
Тогда при ![]() разделим обе части уравнения на
разделим обе части уравнения на ![]() :
:
![]()
Для того, чтобы данное уравнение имело два корня, один из которых больше 1, а другой меньше 1, нужно чтобы соответствующая парабола, ветви которой направлены вверх, пересекала прямую ![]() в точке, ордината которой лежит ниже оси OY. То есть должно быть выполнено условие:
в точке, ордината которой лежит ниже оси OY. То есть должно быть выполнено условие:
![]()
После всех преобразований получаем:
![]()
Решением этого неравенства является промежуток:
![]() .
.
Подготовка к вступительному экзамену по математике в РЭУ им. Г.В. Плеханова
Если вам требуется подготовка к вступительному экзамену по математике в РЭУ им. Г.В. Плеханова, вы можете обратиться к репетитору, профессионально занимающемуся подготовкой абитуриентов к этому экзамену. Возможны как очные занятия, так и занятия через интернет.


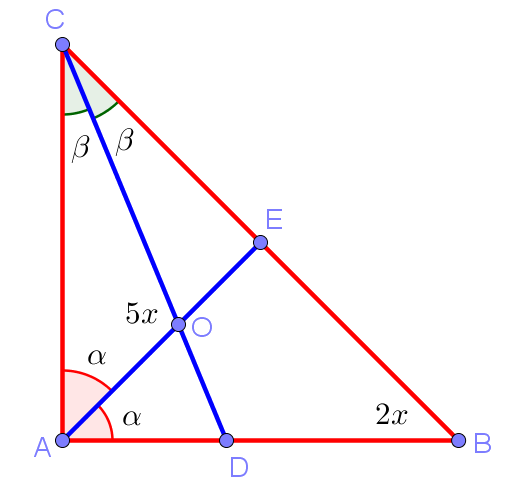
в 9 задаче ****Биссектрисы AP и CM пересекаются в точке O****
описка : точки D и Е
Да, спасибо, исправил в условии.
Очень интерсено,толково ,обстоятельно Спасибо.
Я Ваши ролики советую своим ученикам.
Рад, что Вы меня смотрите и советуете своим ученикам. Скоро выйдут новые ролики по методу рационализации в логарифмических неравенствах и в неравенствах с модулем. Как раз для новоиспечённых одиннадцатиклассников, чтобы к ЕГЭ по математике готовились)
я не понял
10 той задаче вы сказали что ветви параболы направлены вверх.
но по ответу (-бесконечность;-4)
ветви параболы направлены вниз
как это?
Ветви параболы, которая получилась после деления обеих частей на 2a, направлены вверх.
Добрый вечер, Сергей Валерьевич. Вероятно, мой вопрос покажется глупым, но всеже. Я все никак не возьму в толк, как Вы в первом задании получили 27/8 под корнем из дроби 3 целых 3/8. Если я правильно помню, при умножении целого числа на дробь, умножается только числитель, а знаменатель остается неизменным. В таком случае, должно получиться 9/8 (3*3=9) или я что-то перепутал? Спасибо.
есть 3 целых. Если у нас стоит дробь 3/8, значит 1 целая равна 8/8. Так как их у нас 3, то мы просто 8*3, получаем число 24 и складываем с 3 и получаем 27/8. Да, если бы мы умножали целое число на дробь, то получилось бы 9/8, как ты написал выше, но это число скорее, как 2,5, а не 2*0,5.
Сообразил, прошу прощения, это было не умножение а число :))
Не важно