Вступительный экзамен по математике в МГУ

Автор

Четверг, 2 августа, 2012

Поступление в МГУ - экзамен по математике

Стать студентом МГУ мечтают многие школьники и абитуриенты. Этот университет по праву считается первым вузом страны. При этом известно, что диплом Московского государственного университета котируется не только в России, но и за рубежом. Всё это, безусловно, не может не отразиться на конкурсе при поступлении. Одним из вступительных экзаменов на механико-математический, экономический и ряд других факультетов МГУ является экзамен по математике. В 2012 году приемные комиссии университета принимали результаты Единого государственного экзамена (ЕГЭ). Однако, помимо этого, абитуриенты традиционно сдавали внутренний вступительный экзамен по математике, который проводился в письменной форме и оценивался, как и ЕГЭ, по 100-балльной шкале.

В 2012 году вступительный экзамен по математике в МГУ проводился централизованно для абитуриентов всех факультетов и засчитывался на все специальности, на которые абитуриент подал документы о поступлении. По словам организаторов, на экзамене к поступающим не предъявлялось никаких требований, выходящих за рамки программы средней школы. Однако было также отмечено, что уровень сложности предлагаемых заданий был достаточно высок. Предлагаю вам оценить его самостоятельно. В данной статье приведен подробный разбор заданий одного из вариантов вступительного экзамена по математике в МГУ в 2012 году.

Задание 1. Найдите многочлен второй степени, если известно, что его корни равны -\frac{5}{7} и \frac{9}{4}, а свободный член равен -5.

Решение. Многочлен второй степени, у которого свободный член равен -5, имеет вид: ax^2+bx-5. При этом a\ne 0, поскольку в противном случае у него не могло бы быть двух корней. Поскольку -\frac{5}{7} и \frac{9}{4} — корни многочлена, то согласно теореме Виета имеет место система:

    \[ \begin{cases} \frac{25}{49}a-\frac{5}{7}b-5 = 0, \\ \frac{81}{16}a+\frac{9}{4}b-5 = 0\end{cases}\Leftrightarrow \begin{cases}a=\frac{28}{9}, \\ b=-\frac{43}{9}.\end{cases} \]

Ответ: \frac{28}{9}x^2-\frac{43}{9}x-5.

Задание 2. Вычислите:

    \[ \log_3\left(-\log_6\frac{7}{1512}\right). \]

Решение. Тут нужно просто правильно посчитать:

    \[ \log_3\left(-\log_6\frac{7}{1512}\right) = \log_3\left(-\log_6\frac{1}{216}\right) = \]

    \[ = \log_3\left(-\log_6 6^{-3}\right) = \log_3 3 = 1.\right) \]

Задание 3. Решите неравенство:

    \[ (4^x-2^{x+3}+15)\sqrt{3^x-9}\geqslant 0. \]

Решение. Подкоренное выражение не может принимать отрицательных значений. Сам корень также неотрицателен, значит неотрицательным должно быть выражение, стоящее в скобках. Таким образом исходное неравенство равносильно следующей системе неравенств:

    \[ \begin{cases} 4^x-2^{x+3}+15\geqslant 0, \\ 3^x-9\geqslant 0\end{cases}\Leftrightarrow\begin{cases}2^{2x}-8\cdot 2^x+15\geqslant 0, \\ x\geqslant 2\end{cases} \]

    \[ \begin{cases}\left[\begin{array}{l}2^x\leqslant 3, \\ 2^x\geqslant 5,\end{array} \\ x\geqslant 2\right.\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l}x\leqslant \log_2 3, \\ x\geqslant \log_2 5,\end{array} \\ x\geqslant 2\right.\end{cases}\Leftrightarrow \left[\begin{array}{l}x = 2, \\ x\geqslant\log_2 5.\end{array}\right. \]

Ответ: x\in\{2\}\cup\left[\log_2 5;+\mathcal{1}\right).

Задание 4. Решите уравнение:

    \[ \cos 4x+\cos 2x-\cos 3x\cdot \sqrt{2}=0. \]

Решение. Используем формулу суммы косинусов:

    \[ 2\cos 3x\cos x-\sqrt{2}\cos 3x = 0\Leftrightarrow \]

    \[ \cos 3x (2\cos x-\sqrt{2})=0\Leftrightarrow\left[\begin{array}{l}\cos 3x = 0, \\ \cos x = \frac{\sqrt{2}}{2}.\end{array}\right. \]

Ответ: \frac{\pi}{6}+\frac{\pi k}{3},\,\pm\frac{\pi}{4}+2\pi n.

Задание 5. Найдите площадь фигуры, состоящей из множества всех точек (x;y), удовлетворяющих уравнению:

    \[ |2x+y|+|y|+2|x-1|=2. \]

Решение. При любом раскрытии модулей получается уравнение прямой линии, площадь которой равна 0. Кроме случая, когда:

    \[ \begin{cases}2x+y>0, \\ x-1<0, \\ y<0\end{cases}\Leftrightarrow \begin{cases}y>-2x, \\ x<1, \\ y<0.\end{cases} \]

Этими условиями определяется следующая область на координатной плоскости:

Рисунок к задаче №5 из вступительного экзамена в МГУ по математике в 2012 году

Область на координатной плоскости, определяемая данной системой

В этом случае при раскрытии модулей получается 0=0, то есть все точки полученной области удовлетворяют данному уравнению. Площадь соответствующего треугольника равна 1.

Ответ: 1.

Задание 6. Центр окружности лежит на стороне BC треугольника ABC. Окружность касается сторон AB и AC в точках D и E соответственно и пересекает сторону BC в точках F и G (точка F лежит между точками B и G). Известно, что BF=1, а \frac{BD}{DA}=\frac{AE}{EC}=\frac{1}{2}. Найти отрезок CG.

Решение.

Рисунок к задаче по планиметрии из вступительного экзамена по математике в МГУ 2012

Рисунок к задаче

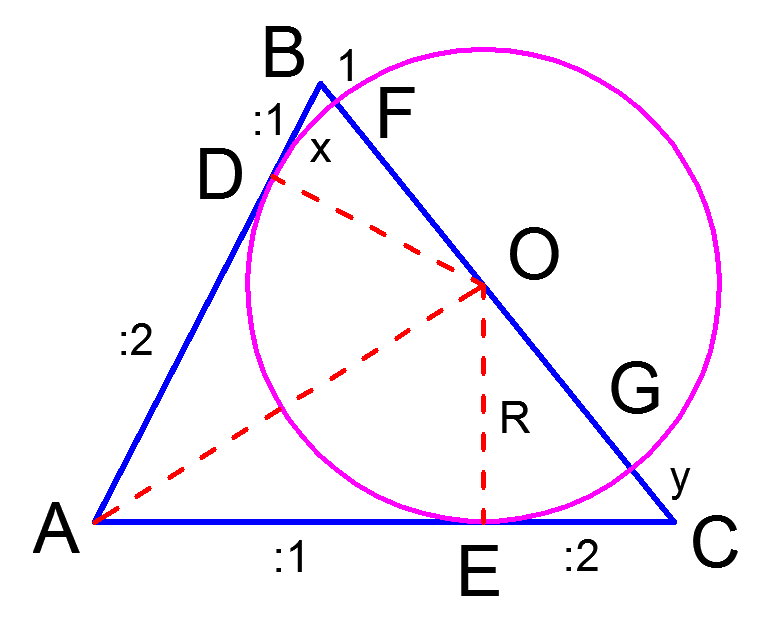
Центр вписанной в угол окружности O лежит на биссектрисе AO угла A. Биссектриса треугольника делит противолежащую сторону треугольника на отрезки, пропорциональные сходственным сторонам, то есть \frac{BO}{AB} = \frac{OC}{AC}. Радиус окружности, проведенный в точку качания, перпендикулярен касательной, то есть \angle ODB = 90^0, \angle OEC = 90^0.

Введем обозначения: R — радиус окружности, BD = x, y — длина искомого отрезка GC. AD = 2 BD = 2x. AD = AE = 2x — отрезки касательных. EC = 2AE = 4x. Из теоремы Пифагора для прямоугольных треугольников BDO и OEC и упомянутой выше теоремы о биссектрисе треугольника получаем следующую систему уравнений:

    \[ \begin{cases}R^2+x^2 = (R+1)^2, \\ R^2+16x^2=(R+y)^2, \\ \frac{R+y}{R+1}=2.\end{cases} \]

Из последнего уравнения получаем: R+y = 2(R+1), подставляем это выражение во второе уравнение системы и получаем:

    \[ \begin{cases}R^2+x^2 = (R+1)^2, \\ R^2+16x^2=4(R+1)^2.\end{cases} \]

Из первого уравнения получаем: x^2 = (R+1)^2-R^2 = 2R+1. Подставляем это во второе уравнение и получаем:

    \[ R^2 +16(2R+1) = 4(R+1)^2. \]

После всех преобразований и вычислений получаем: R = 4+2\sqrt{5}, ну а тогда с учетом R+y = 2(R+1) получаем y = R+2 = 6+2\sqrt{5}.

Ответ: 6+2\sqrt{5}.

Задание 7. Определите, при каких значениях параметра a уравнение

    \[ a\sqrt{x+y}=\sqrt{x}+\sqrt{3y} \]

имеет единственное решение (x;y).

Решение. Заметим, что пара (0;0) является решением исходного уравнения при любом значении a. Поэтому выясним, при каком значении параметра a исходное уравнение имеет единственное решение (0;0).

1. При a\leqslant 0 левая часть исходного уравнения неположительна, а правая — неотрицательна. Поэтому решение может быть только в том случае, если обе части равны нулю. Это условие выполняется только при x=0 и y=0. Итак, при a\leqslant 0 исходное уравнение имеет единственное решение.

2. При a>0 имеем:

    \[ \left(a\sqrt{x+y}\right)^2=\left(\sqrt{x}+\sqrt{3y}\right)^2\Rightarrow \]

    \[ \left(a^2-1\right)x+\left(a^2-3\right)y=2\sqrt{3xy}. \]

Можно показать, что при a>0 последнее уравнение имеет отличное от (0;0) решение при a\in [1;2]. Итак, при a>0 исходное уравнение имеет единственное решение (0;0) при a\in(0;1)\cup(2;+\mathcal{1}).

Объединяя полученные в п.1 и п.2 решения, получаем окончательный ответ a\in(=\mathcal{1};1)\cup(2;+\mathcal{1}).

Ответ: a\in(=\mathcal{1};1)\cup(2;+\mathcal{1}).

Задание 8. В основании пирамиды лежит правильный треугольник АВС со стороной, равной \sqrt{3}, боковые ребра AS, BS, CS пирамиды равны соответственно 4, 4 и 5. Прямой круговой цилиндр расположен так, что окружность его верхнего основания имеет ровно одну общую точку с каждой из боковых граней пирамиды, а окружность нижнего основания лежит в плоскости АВС и касается ровно одного из ребер основания пирамиды. Найти радиус основания цилиндра.

Решение. Чертеж — самая сложная часть решения данной задачи:

Вступительный экзамен МГУ (стереометрия) - чертеж к заданию

Чертеж к задаче

Итак, пусть M — точка касания нижнего основания цилиндра с ребром AB пирамиды SABC. Верхнее основание цилиндра вписано в равносторонний треугольник A1B1C1, следовательно, центр верхнего основания лежит на биссектрисе C1N угла A1C1B1, а значит и центр нижнего основания лежит на биссектрисе CM угла ACB, то есть CM — одновременно и медиана, то есть M — середина стороны AB.

Из теоремы Пифагора для треугольников ACM и SAM находим CM = \frac{3}{2} и SM = \frac{\sqrt{61}}{2}. По теореме косинусов для треугольника SCM находим \cos\angle C = \frac{4}{5}, откуда SO = 3, CO = 4, MO = \frac{5}{2}, \operatorname{tg}\angle SMO = \frac{6}{5}. (все промежуточные вычисления рекомендуется проделать самостоятельно).

Пусть искомый радиус равен r, тогда NK = CO-CM-ME = 40-\frac{3}{2}-2r = \frac{5-4r}{2}. SK = NK\operatorname{tg}\angle SMO = \frac{15-12r}{5}. Из подобия треугольников SC1N и SCM подучаем, что \frac{C_1N}{CM}=\frac{SK}{SO}, то есть \frac{2\cdot 3r}{3}=\frac{15-12r}{5\cdot 3}, откуда получаем r = \frac{5}{14}.

Ответ: \frac{5}{14}.

Сергей Валерьевич
Репетитор для подготовки к вступительному
экзамену по математике в МГУ

Метки: , ,
Опубликовано в категории Методическая копилка | 5 комментариев »

Комментарии

  1. Асель:
    05.07.2013 в 14:16

    Спасибо за полезную информацию!

  2. Эльвин:
    05.07.2013 в 19:38

    Спасибо большое!Все четко и понятно.

  3. ivan:
    23.11.2013 в 01:02

    а разве можно пользоваться производной?

    1. Sergey Seliverstov:
      23.11.2013 в 10:46

      А почему нельзя? Там в решении нет ничего такого, что не изучалось бы в школьном курсе математики.

  4. Мария:
    15.07.2014 в 16:08

    Спасибо