
История школы №1535 берёт своё начало в 1929 году, когда её здание было построено по проекту известного советского архитектора Михаила Ивановича Мотылева. Новейшая история школы 1535 началась в 1991, когда был открыт лицей с направлениями подготовки в сфере востоковедения при Институте Стран Африки и Азии МГУ. Численность обучающихся достигала 350 человек, а лицей был открыт в качестве эксперимента.
В 2004-2005 годах учреждение было основательно модернизировано, было достроено 2 дополнительных корпуса, укреплены стены и заменены старые перекрытия. Количество учеников постоянно росло. После соединения со школой №35 в 2010 году оно составило около 1000, а в 2017 году — уже 1300.
Школа №1535 сменила 6 человек на посту главного директора. На данный момент им является Сергей Сергеевич Сехин, который ранее заведовал школой №1210 Северо-Западного АО Москвы.
Образовательное учреждение на сегодняшний день предоставляет на выбор 3 профиля обучения для обучающихся 7-9 классов:

Для абитуриентов, поступающих в 10 и 11 классы, спектр доступных профилей обучения существенно расширяется:

Качество образования в школе №1535 представлено на высоком уровне. Учреждение занимало первое место в рейтинге по предоставляемому качеству образования среди школ Москвы и России в 2006, 2011, 2013 и 2018 годах. Также образовательное учреждение занимало призовые места в конкурсах лучших школ в 2010, 2017 годах. Школа стабильно поддерживает высокие баллы ЕГЭ учеников и раскрывает потенциал каждого представленного направления.
Такой результат сложился благодаря высокому уровню организации обучения, ориентированности преподавателей на плодотворную работу с учениками и готовности учеников к тяжелому умственному труду, а также помощи администрации города в развитии школы.

Поступление в школу 1535 осуществляется на конкурсной основе и сопровождается из года в год огромной конкуренцией среди абитуриентов. Из-за этого на вступительном экзамене недостаточно будет решить пару задач. Необходимо выжать максимум из своих знаний.
Типы вступительных экзаменов варьируются в зависимости от выбранного направления подготовки, но основными являются экзамен по русскому языку и математике. На сайте школы есть демонстрационные варианты экзаменов, а в арсенале профессиональных репетиторов, осуществляющих подготовку к поступлению в школу 1535, есть примеры экзаменов предыдущих лет, которые помогут сделать подготовку к сдаче вступительных экзаменов максимально эффективной.
После сдачи экзаменов на сайте школы можно узнать результаты. Если поступающий не достиг проходного балла по какому-либо из вступительных испытаний, то его номер абитуриента будет скрыт в личном кабинете. В случае возникновения проблем и вопросов по поступлению вы можете обратиться в приёмную комиссию, при этом указав имя, фамилию и номер класса, в который поступаете.
Даты проведения вступительных испытаний устанавливаются приёмной комиссией и обычно находятся в промежутке март-апрель текущего года. План набора в образовательное учреждение на текущий год публикуется на сайте школы не позднее пятнадцатого января текущего года приёма, а окончание утверждения плана набора производится после завершения вступительных испытания и до публикации решения приёмной комиссии. При поступлении также учитываются индивидуальные достижения и льготы, а также результаты участия в различных олимпиадах.

Для подготовки к поступлению в школу №1535 можно воспользоваться специальными платными образовательными курсами, описание и стоимость которых можно найти в Интернете в открытом доступе. Однако, как показывает практика, такая форма подготовки мало чем отличается от обычных школьных занятий и редко позволяет ученику достичь требуемого уровня. Фактически, большинство учащихся на этих курсах так и не становятся учениками школы 1535, поскольку не сдают вступительные экзамены на должном уровне.
Самостоятельной подготовки также может оказаться недостаточно. В силу отсутствия опыта или высокой загруженности при обучении в другом образовательном учреждении абитуриент может не суметь правильно организовать учебный процесс самостоятельно. В таких случаях на помощь придёт репетитор, имеющий определённый опыт и методику образования.
Поступление в школу 1535 с репетитором может стать осуществимым благодаря грамотному распределению времени и структурированию информации. Опытный репетитор имеет в своём распоряжении проверенную годами методику подготовки абитуриентов к поступлению в школу 1535, которая позволяет подготовиться к успешной сдаче вступительных экзаменов за ограниченный промежуток времени. Также опытный репетитор имеет множество варианты заданий вступительных экзаменов прошлых лет, решая которые ученик получит дополнительную тренировку.
В помощь тем, кто готовится к вступительным экзаменам в школу 1535, ниже приведён разбор демонстрационного варианта вступительного экзамена в 10 класс от профессионального репетитора по математике, занимающегося подготовкой школьников к поступлению в школу 1535. Его контакты можно найти на этой странице. Изучите представленный разбор. Это будет очень полезно.
Задание 1. Упростите выражение 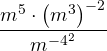 , приведя его к виду , приведя его к виду |
Не ошибитесь! Обратите внимание, что ![]() , так как в квадрат возводится только число
, так как в квадрат возводится только число ![]() , а не число
, а не число ![]() . Тогда, используя свойства степеней, получаем следующее:
. Тогда, используя свойства степеней, получаем следующее:
![]()
Ответ: 15.
| Задание 2. Вычислите
|
Считаем числитель:
![]()
Считаем знаменатель:
![Rendered by QuickLaTeX.com \[ \left(\dfrac{1}{2}\right)^{-2}-5\cdot \dfrac{1}{(-2)^2}+\left(\dfrac{3}{2}\right)^2 = \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-cefcfafbca5d924f414d0cdf0f060137_l3.png)
![]()
Тогда получаем окончательный ответ:
![]()
Ответ: 0.25.
Задание 3. На рисунке изображён график движения туриста из города A в город B. Определите скорость туриста (в км/ч) после привала.
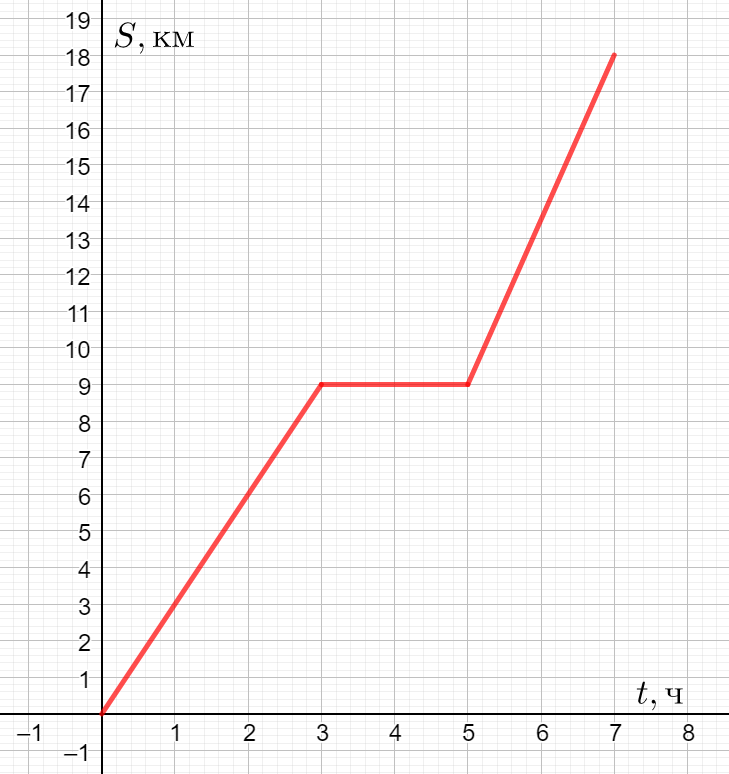 |
Привал был во временном промежутке с 3 до 5 ч. Далее за промежуток времени с 5 до 7 часов, то есть за 2 ч, турист прошёл 18-9 = 9 км. Значит, его скорость была равна 9 : 2 = 4.5 км/ч.
Ответ: 4.5.
| Задание 4. Найдите значение выражения |
Упрощаем выражение:
![]()
Ответ: -5.
| Задание 5. Чему равно наименьшее значение выражения |
Рассмотрим функцию ![]() . Графиком этой функции является парабола, ветви которой направления вверх. Значит, своё наименьшее значение эта функция достигает в вершине данной параболы.
. Графиком этой функции является парабола, ветви которой направления вверх. Значит, своё наименьшее значение эта функция достигает в вершине данной параболы.
Ищем абсциссу этой вершины:
![]()
Подставляем это значение в уравнение параболы и находим ординату вершины. Это и будет наименьшее значение исходного выражения:
![]()
Ответ: -5.
| Задание 6. Найдите сумму всех различных корней уравнения
|
Знаменатель не может обращаться в нуль, поэтому данное уравнение имеет смысл только при ![]() , то есть при
, то есть при ![]() . Для этих значений исходное уравнение эквивалентно следующему:
. Для этих значений исходное уравнение эквивалентно следующему:
![]()
То есть либо ![]() , то есть
, то есть ![]() . Либо
. Либо ![]() . Для решения последнего уравнения используем замену:
. Для решения последнего уравнения используем замену: ![]() . Тогда получаем уравнение
. Тогда получаем уравнение ![]() , единственным положительным корнем которого является число
, единственным положительным корнем которого является число ![]() . Возвращаясь к исходной переменной, получаем, что
. Возвращаясь к исходной переменной, получаем, что ![]() , то есть
, то есть ![]() или
или ![]() . Корень
. Корень ![]() не входит в область допустимых значений.
не входит в область допустимых значений.
Итак, у исходного уравнения ровно 2 корня: 0.03 и -5. Сумма полученных корней равна -4.97.
Ответ: -4.97.
| Задание 7. Решить систему уравнений
|
Выразим из второго уравнения системы ![]() . Получаем, что
. Получаем, что ![]() . Теперь подставим полученное значение
. Теперь подставим полученное значение ![]() в первое уравнение:
в первое уравнение:
![]()
![]()
Получаем, что ![]() и
и ![]() . Соответствующие значения
. Соответствующие значения ![]() равны
равны ![]() и
и ![]() . Значит, решениями системы являются пары чисел
. Значит, решениями системы являются пары чисел ![]() и
и ![]() . Так как
. Так как ![]() , то ответ
, то ответ ![]() .
.
Ответ: 1.5.
| Задание 8. В растворе спирта и воды спирта в четыре раза меньше, чем воды. Когда к этому раствору добавили 20 литров воды, получили 12%-ый раствор спирта. Сколько литров воды было в исходном растворе? |
Пусть в исходном растворе было ![]() л воды. Тогда спирта в нём
л воды. Тогда спирта в нём ![]() . Так как после добавления 20 л воды концентрация спирта составила 12%, то имеет место уравнение:
. Так как после добавления 20 л воды концентрация спирта составила 12%, то имеет место уравнение:
![Rendered by QuickLaTeX.com \[ 0.12 = \dfrac{\dfrac{x}{4}}{\dfrac{x}{4}+x+20} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-23afc27e759cc4d5e18b888f5dd61bb7_l3.png)
![]()
![]()
![]()
Ответ: 24.
| Задание 9. Упростить выражение
|
Выполняем действия в скобках:
![]()
![Rendered by QuickLaTeX.com \[ = \dfrac{(m+1)^2-(m+3)}{(m-1)(m+1)(m+3)} =\]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-d4a539451060c6f2cf25b8b490440f48_l3.png)
![Rendered by QuickLaTeX.com \[ = \dfrac{m^2+2m+1-m-3}{(m-1)(m+1)(m+3)} = \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-04a88a6e0b7863a87c78b046fcf1fbe3_l3.png)
![Rendered by QuickLaTeX.com \[ =\dfrac{m^2+m-2}{(m-1)(m+1)(m+3)} = \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3e3b0b06624fdd3ad376d2390a27ba0c_l3.png)
![]()
Выполняем деление:
![]()
![]()
То есть в области допустимых значений результат не зависит от ![]() и всегда равен.
и всегда равен.
Ответ: 1.
| Задание 10. В прямоугольную трапецию вписана окружность. Точка касания окружности с боковой стороной делит эту сторону на отрезки 4 и 9. Найдите площадь трапеции. |
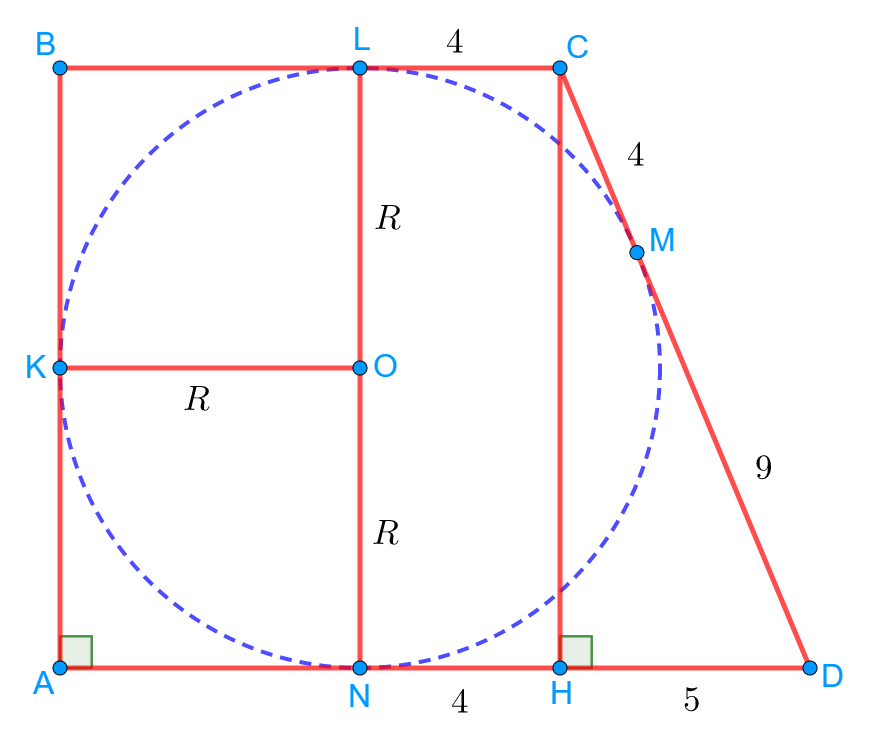
Проведём высоту CH данной трапеции. Так как ND = DM = 9 (теорема об отрезках касательных), и LC = NH (так как четырёхугольник LCHN является прямоугольником), то HD = ND — NH = 5.
Тогда из прямоугольного треугольника CHD находим по теореме Пифагора, что CH = 2R = 12, где R = 6 — радиус вписанной окружности. Тогда BC = R + LC = 10. Аналогично, AD = R + ND = 15. Тогда искомая площадь трапеции равна CH ⋅ (AD + BC) / 2 = 150.
Ответ: 150.
| Задание 11. А) Решите систему неравенств
|
А) Так как ![]() , то исходная система эквивалентна следующей:
, то исходная система эквивалентна следующей:
![Rendered by QuickLaTeX.com \[ \begin{cases} t^2-6t+5\leqslant 0 \\ t^2-8t+15 > 0 \end{cases}\Leftrightarrow \begin{cases} (t-1)(t-5)\leqslant 0 \\ (t-3)(t-5) > 0 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b44fbb479a427222e6d8fd6d0127783b_l3.png)
Пересечение решений каждого из неравенств даёт результат: ![]() .
.
Б) Сумма целочисленных решений системы неравенств равна: ![]() .
.
Ответ: А) ![]() ; б) 3.
; б) 3.
| Задание 12. Первый тракторист вспахивает поле на 2 часа быстрее второго. А, работая вместе, эти трактористы вспахивают то же поле за |
Кажется, что задача выглядит сложно, но всё станет проще, если готовиться к поступлению в школу 1535 с репетитором.
Пусть второй тракторист может вспахать поле за ![]() часов. Тогда первый тракторист может вспахать поле за
часов. Тогда первый тракторист может вспахать поле за ![]() часа. Значит, за 1 час первый тракторист вспахивает
часа. Значит, за 1 час первый тракторист вспахивает ![]() часть поля, а второй —
часть поля, а второй — ![]() часть поля. Значит, работая вместе, трактористы вспахивают
часть поля. Значит, работая вместе, трактористы вспахивают ![]() часть поля. Так как, работая вместе, трактористы могут вспахать поле за
часть поля. Так как, работая вместе, трактористы могут вспахать поле за ![]() часа, то имеет место уравнение:
часа, то имеет место уравнение:
![]()
![]()
![Rendered by QuickLaTeX.com \[ \dfrac{8x^2-46x+30}{15x(x-2)}=0 \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3af51fdc9770c45d4cbc7143a00c498e_l3.png)
![]()
Последнее уравнение имеет два корня: ![]() и
и ![]() , но корень
, но корень ![]() не подходит по смыслу задачи (иначе время работы первого тракториста отрицательно). Итак, второй тракторист справится с работой за 5 ч.
не подходит по смыслу задачи (иначе время работы первого тракториста отрицательно). Итак, второй тракторист справится с работой за 5 ч.
Ответ: 5.
| Задание 13. На стороне AB параллелограмма ABCD как на диаметре построена окружность, проходящая через точку пересечения диагоналей и через середину стороны AD. Найдите градусную меру угла ACB. |
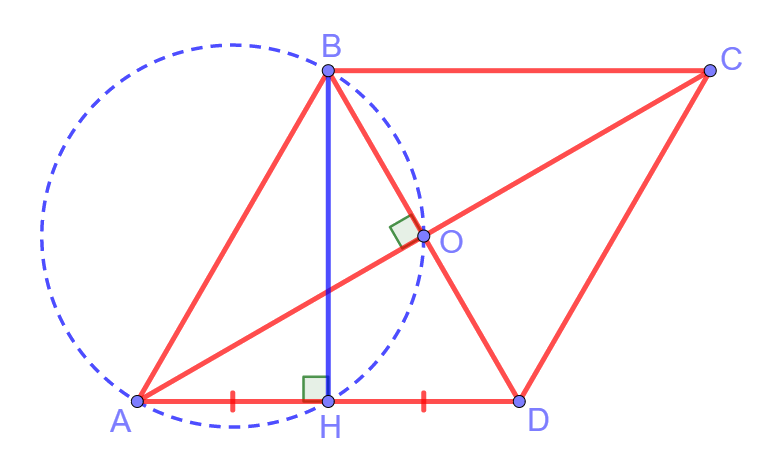
Вписанные углы AHB и AOB прямые, так как они опираются на диаметр. В треугольнике ABD высота BH является медианой. Значит, треугольник ABD равнобедренный с основанием AD, и AB = BD. Диагонали параллелограмма точкой пересечения делятся пополам, поэтому BO = OD. То есть в треугольнике ABD высота AO является медианой. Значит, треугольник DAB равнобедренный с основанием BD, и AD = AB. Итак, получили AB = BD = AD, то есть треугольник ABD равносторонний.
То есть угол A равен 60 градусам. Так как AO является высотой равностороннего треугольника, то она также является и биссектрисой угла A. То есть угол OAB равен 30 градусам. Кроме того, угол OAD равен углу ACB, так как они являются накрест лежащими при параллельных прямых AD, BC и секущей AC. Итак, градусная мера угла ACB равна 30 градусам.
Ответ: 30.
| Задание 14. а) Найдите значение б) Постройте график функции в) Укажите промежуток убывания функции г) Найдите все значения параметра |
а) Иными словами требуется найти значение ![]() , при котором абсцисса вершины параболы равна
, при котором абсцисса вершины параболы равна ![]() . То есть имеет место уравнение:
. То есть имеет место уравнение:
![]()
Из этого уравнения получаем, что ![]() .
.
б) При данном значении ![]() получаем следующую функцию:
получаем следующую функцию: ![]() , график которой изображен на рисунке:
, график которой изображен на рисунке:
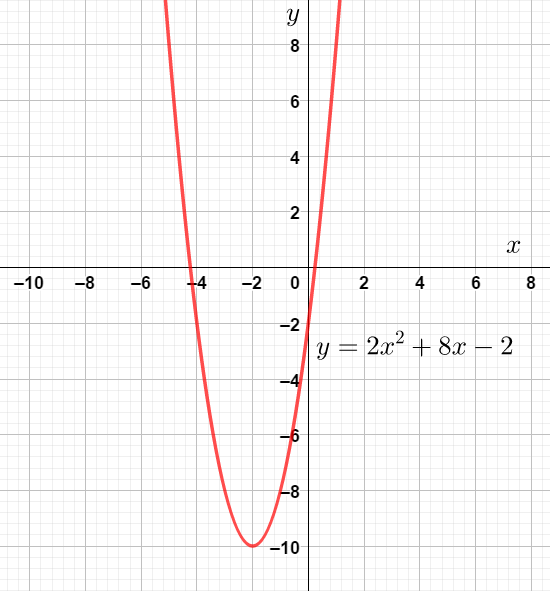
в) Из графика видно, что функция убывает при ![]() .
.
г) Ищем значения параметра ![]() такие, что уравнение
такие, что уравнение
![]()
имеет единственное решение. После упрощения получаем следующее уравнение:
![]()
Его дискриминант должен быть равен нулю. То есть получаем уравнение: ![]() , откуда
, откуда ![]() . Значит, при этом значении
. Значит, при этом значении ![]() прямая
прямая ![]() касается графика функции f (имеет с ним одну единственную общую точку. При бОльших значениях
касается графика функции f (имеет с ним одну единственную общую точку. При бОльших значениях ![]() прямая будет находиться ниже графика функции f и не будет иметь с ним ни одной общей точки. Этот случай также подходит. При остальных значениях
прямая будет находиться ниже графика функции f и не будет иметь с ним ни одной общей точки. Этот случай также подходит. При остальных значениях ![]() будет две точки пересечения.
будет две точки пересечения.
Итак, прямая ![]() имеет с графиком функции ( f ) не более одной общей точки при
имеет с графиком функции ( f ) не более одной общей точки при ![]() .
.
Если вам требуется подготовка к вступительным экзаменам по математике в школу 1535, обращайтесь ко мне. Я являюсь репетитором и профессионально занимаюсь такого рода подготовкой уже много лет. Мои контакты вы найдёте на этой странице.
Материал подготовил репетитор для подготовки к поступлению в школу 1535 в Москве Сергей Валерьевич