 Статья посвящена разбору примеров решения неравенств методом интервалов. При том, что этот метод решения неравенств достаточно универсален, важно помнить, что не всегда применение данного метода оправдано с точки зрения объема вычислений. Иногда бывает удобнее воспользоваться некоторыми другими методами решения неравенств. Все рассмотренные в статье неравенства взяты из реальных вариантов ЕГЭ по математике разных лет. Присутствует подробный видеоразбор одного из заданий.
Статья посвящена разбору примеров решения неравенств методом интервалов. При том, что этот метод решения неравенств достаточно универсален, важно помнить, что не всегда применение данного метода оправдано с точки зрения объема вычислений. Иногда бывает удобнее воспользоваться некоторыми другими методами решения неравенств. Все рассмотренные в статье неравенства взяты из реальных вариантов ЕГЭ по математике разных лет. Присутствует подробный видеоразбор одного из заданий.
Метод интервалов
Пусть заданное неравенство имеет вид: ![]() Для решения этого неравенства используется так называемый метод интервалов (метод промежутков), который состоит в следующем.
Для решения этого неравенства используется так называемый метод интервалов (метод промежутков), который состоит в следующем.
Во-первых, на числовую ось наносят точки ![]() разбивающие ее на промежутки, в которых выражение
разбивающие ее на промежутки, в которых выражение ![]() определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений
определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений ![]() и
и ![]() Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками — точки, удовлетворяющие заданному неравенству, а светлыми кружками — не удовлетворяющие ему.
Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками — точки, удовлетворяющие заданному неравенству, а светлыми кружками — не удовлетворяющие ему.
Во-вторых, определяют и отмечают на числовой оси знак выражения ![]() для значении
для значении ![]() , принадлежащих каждому из полученных промежутков. Если функции
, принадлежащих каждому из полученных промежутков. Если функции ![]() и
и ![]() являются многочленами и не содержат множителей вида
являются многочленами и не содержат множителей вида ![]() где
где ![]() то достаточно определить знак функции
то достаточно определить знак функции ![]() в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.
в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.
Если же в числителе или знаменателе дроби ![]() имеется множитель вида
имеется множитель вида ![]() где
где ![]() то непосредственной проверкой выясняют, удовлетворяет ли значение
то непосредственной проверкой выясняют, удовлетворяет ли значение ![]() заданному неравенству.
заданному неравенству.
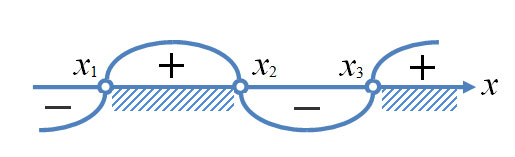
Изменение знаков удобно иллюстрировать с помощью волнообразной кривой (кривой знаков), проведенной через отмеченные точки и лежащей выше или ниже числовой оси в соответствии со знаком дроби ![]() в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. На ту же ось помещают и точки, соответствующие
в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. На ту же ось помещают и точки, соответствующие ![]() Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству.
Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству.
Примеры решения неравенств методом интервалов
![]()
Решение. Упрощаем неравенство путем равносильных преобразований:
![Rendered by QuickLaTeX.com \[ \frac{1}{x^2-5x+6}-\frac{1}{2}\leqslant 0\Leftrightarrow \frac{2-(x^2-5x+6)}{2(x^2-5x+6)}\leqslant 0\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-730734e93796110ee25c6fc4704ef9cd_l3.png)
![]()
Выражения, стоящие в числителе и знаменателе, можно разложить на множители, тогда неравенство примет вид:
![]()
Далее по алгоритму решения неравенств методом интервалов находим корни уравнений ![]() и
и ![]() . Из первого получаем
. Из первого получаем ![]()
![]() Из второго получаем
Из второго получаем ![]()
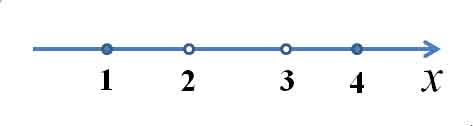
![]() Наносим на числовую прямую получившиеся точки, причем точки
Наносим на числовую прямую получившиеся точки, причем точки ![]() и
и ![]() обозначаем закрашенными кружочками (для них неравенство выполняется), а точки
обозначаем закрашенными кружочками (для них неравенство выполняется), а точки ![]() и
и ![]() — светлыми (для них неравенство не выполняется, при этих значениях, выражение, стоящее слева от знака неравенства, вообще не имеет смысла):
— светлыми (для них неравенство не выполняется, при этих значениях, выражение, стоящее слева от знака неравенства, вообще не имеет смысла):
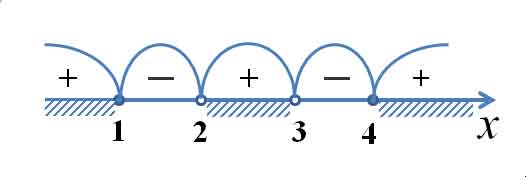
Определяем теперь знаки выражения ![]() на полученных промежутках (подставляем любое значение
на полученных промежутках (подставляем любое значение ![]() из каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется:
из каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется:
Итак, исходному неравенству удовлетворяют следующие значения: ![]()
Ответ: ![]()
Задача для самостоятельного решения №1. Решите неравенство:
![]()
Показать ответ
![]()
Решение. Подкоренное выражение, как известно, не может принимать отрицательных значений, также не допускается нахождение в знаменателе дроби нуля. Следовательно, область допустимых значений данного неравенства определяется неравенством ![]() и тем условием, что
и тем условием, что ![]() Решаем уравнения
Решаем уравнения ![]() и
и ![]() Из первого уравнения получаем, что
Из первого уравнения получаем, что ![]() Из второго уравнения получаем, что
Из второго уравнения получаем, что ![]() Наносим область допустимых значений неравенства и полученные точки на числовую прямую, причем эти точки будет светлыми, поскольку ни одно из значений
Наносим область допустимых значений неравенства и полученные точки на числовую прямую, причем эти точки будет светлыми, поскольку ни одно из значений ![]() и
и ![]() не удовлетворяет неравенству. Сразу определяем знаки выражения
не удовлетворяет неравенству. Сразу определяем знаки выражения ![]() в каждом из полученных промежутков и рисуем кривую знаков:
в каждом из полученных промежутков и рисуем кривую знаков:
Верхней стрелкой на рисунке обозначена область допустимых значений неравенства. Ответом к неравенству будет являться промежуток, соответствующий на рисунке заштрихованной области.
Ответ: ![]()
Задача для самостоятельного решения №2. Решите неравенство:
![]()
Показать ответ
![]()
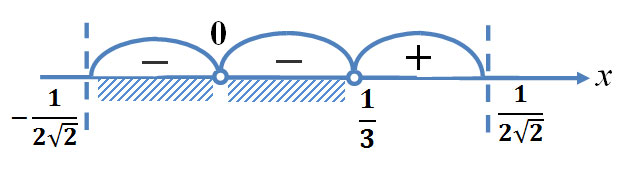
Решение. Подкоренное выражение не может принимать отрицательных значений, а в знаменателе дроби не должно быть нуля. Следовательно, область допустимых значений неравенства определяется следующей системой:
![Rendered by QuickLaTeX.com \[ \begin{cases}1-8x^2\geqslant 0, \\ x\ne 0\end{cases}\Leftrightarrow \begin{cases}-\frac{1}{2\sqrt{2}}\leqslant x\leqslant \frac{1}{2\sqrt{2}}, \\ x\ne 0.\end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c5e2e667374a38c67f95ae6d66f3e3ff_l3.png)
![]()
Решаем уравнение ![]() и
и ![]() Из первого получаем, что
Из первого получаем, что ![]() и
и ![]() Из второго получаем, что
Из второго получаем, что ![]() Наносим полученные точки на числовую прямую, не забывая о том, какие из них следует закрасить, а какие осветлить. Изображаем также на ней область допустимых значений и изображаем кривую знаков:
Наносим полученные точки на числовую прямую, не забывая о том, какие из них следует закрасить, а какие осветлить. Изображаем также на ней область допустимых значений и изображаем кривую знаков:
Пунктирные лини на рисунке ограничивают область допустимых значений неравенства. Заштрихованная область соответствует решению неравенства.
Ответ: ![]()
Задача для самостоятельного решения №3. Решите неравенство:
![]()
Показать ответ
Метод интервалов — универсальный, но не единственный метод решения неравенств. Уметь использовать этот метод, конечно, необходимо, но не достаточно для успешного решения задач по математики. Как репетитор по математике советую вам освоить и другие более частные методы решения неравенств. Успехов вам!
Сергей Валерьевич
Преподаватель математики и физики
© Латинская пословица

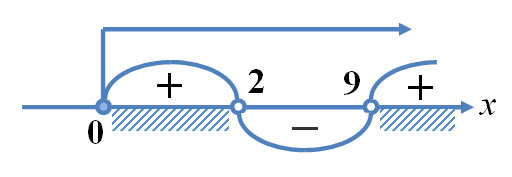
как тут понять если у меня не нуль
Что значит «не нуль»?
не равно нулю,тоесть его нельзя брать,исключи его
Можно написать решения подробней? Плохо понятно,особенно как в третьем получили 1/3:-)
Ну это стандартное иррациональное уравнение. Переносим корень в другую часть уравнения, возводим обе части в квадрат. Получаем квадратное уравнение, решаем его, получаем два корня. Поскольку после возведения обеих частей уравнения в квадрат могут появится посторонние корни, прямой подстановкой в исходное уравнение убеждаемся, что оба полученных корня подходят.
как решить неравенство общего вида?
Методом интервалов.
В третьем примере -1/sqrt(8) тоже должно входить в ответ.
Да, спасибо, исправил.
А почему простого линейного уравнения нету? Можете написать пример линейного уравнения, пожалуйста?
Могу. Ну, например, 4x + 2 > 4. Решаем: 4x > 4 — 2, 4x > 2, x > 0.5
Как определить знаки кривого знаков?
x+4/3+6x<0 ответ (-0.5; 4) ? или я не права?
К неравенству, которое Вы записали, ответ x<-4/21.
Пример1.
Как числитель (и знаменатель) разложить на множители?
Стандартным методом разложения квадратного трехчлена на множители.
в первом примере ,куда мы дели двойку в знаменателе,должны же были умножить эту двойку на скобку
Умножили обе части неравенства на 2, и она сократилась.
Тут неправильно. Знаменатель не может равняться нулю, а значит сразу нужно приравнивать знаменать к нулю, а то, что вы нашли — это неправильно. Посторонние корни
О каком примере речь идет?
ага
Спасибо!!! Очень помогли))
подскажите пож, если в неравенстве в числит и знаменателе квадр. уравнения, в числит имеет реш, а в знаменателе дискрем отриц, получается просто наносим корни числителя и выбираем промежутки?
Если при x^2 коэффициент в знаменателе положительный, то да, так как знаменатель всегда положительный. Если отрицательный — надо ещё поменять знак неравенства, так как знаменатель всегда отрицательный.
А если наоборот: числитель нн имеет корней?
Можете написать как решить неравенство: (х+1-√3)^2 × (х+2-√6) больше 0. Методом интервалов
Корни уравнения (х+1-√3)^2 × (х+2-√6) = 0 равны √3-1 и √6-2. Причём √6-2 находится левее, чем √3-1 на координатной прямой. Определяем знаки на промежутках, на которые эти числа разбивают числовую прямую. Слева направо это будут знаки — + +. Сами точки √6-2 и √3-1 должны изображаться выколотыми, поскольку неравенство строгое. Значит ответ √6-2√3-1.
запишите неравенство, решением которого является объединение числового промежутка и точки. Можете объяснить о чем речь?
Ну, например, вот такое: x^2(x+2)<=0. Его решением является объединение промежутка и точки: x∈(-∞;-2]U{0}.
Что делать, если в числителе кв. уравнение не имеет корней?
В этом случае, если коэффициент a>0, то числитель принимает только положительные значения, если a<0, то только отрицательные. Надо это учесть при расстановке знаков на числовой прямой.
А не подскажите, если в числителе x^3+2x^2+x, то он будет равен 1?
Здравствуйте
Здравствуйте, Алия
Помогите срочно пожалуйста 4х-х-3= >0
Почему нет кв. неравенства вида
(3x + 2)(x — 5)(4x — 1) > 0
Сколько промежутков :
(х-1)(х-2)(х-3)(х-4)(х-55)=0