Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению показательных уравнений и неравенств. В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе.
Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике «Методическая копилка репетитора по физике и математике» в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Прежде чем приступить к разбору конкретных показательных уравнений и неравенств, как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится.
Показательная функция
Что такое показательная функция?
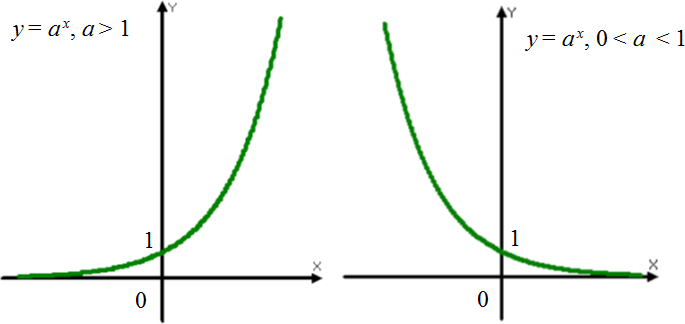
Функцию вида y = ax, где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции y = ax:
| Свойство | a > 1 | 0 < a < 1 |
| Область определения | D(f) = (-∞; +∞) | D(f) = (-∞; +∞) |
| Область значений | E(f) = (0; +∞) | E(f) = (0; +∞) |
| Монотонность | Возрастает | Убывает |
| Непрерывность | Непрерывная | Непрерывная |
График показательной функции
Графиком показательной функции является экспонента:
Решение показательных уравнений
Показательными называются уравнения, в которых неизвестная переменная находится только в показателях каких-либо степеней.
Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
Теорема 1. Показательное уравнение af(x) = ag(x) (где a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).
Помимо этого, полезно помнить об основных формулах и действиях со степенями:
![Rendered by QuickLaTeX.com \[ \fbox{\begin{array}{l} a>0,\, b>0: \\ a^0 = 1, 1^x = 1; \\ a^{\frac{k}{n}}=\sqrt[n]{a^k} \, (k\in Z,\, n\in N);\\ a^{-x} = \frac{1}{a^x}; \\ a^x\cdot a^y = a^{x+y}; \\ \frac{a^x}{a^y}=a^{x-y}; \\ (a^x)^y = a^{xy}; \\ a^x\cdot b^x = (ab)^x; \\ \frac{a^x}{b^x}=\left(\frac{a}{b}\right)^x.\\ \end{array}} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-0e6e38f6336c562d6f1acb899c3f4131_l3.png)
Пример 1. Решите уравнение:
Решение: используем приведенные выше формулы и подстановку:
Уравнение тогда принимает вид:
Дискриминант полученного квадратного уравнения положителен:
![]()
Это означает, что данное уравнение имеет два корня. Находим их:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l} t_1 = \frac{-b+\sqrt{D}}{2a} = \frac{-(-5)+\sqrt{729}}{2\cdot 2}} = 8, \\ t_2 = \frac{-b-\sqrt{D}}{2a} = \frac{-(-5)-\sqrt{729}}{2\cdot 2}} = -5,5. \\ \end{array}\right. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-621cf4590fe29349cf9707d9550ba16f_l3.png)
Переходя к обратной подстановке, получаем:
![]()
Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:
![]()
С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию.
Ответ: x = 3.
Пример 2. Решите уравнение:
Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 94-x положительна и не равна нулю).
Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней:
Последний переход был осуществлен в соответствии с теоремой 1.
Ответ: x = 6.
Пример 3. Решите уравнение:
Решение: обе части исходного уравнения можно поделить на 0,2x. Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид:
Ответ: x = 0.
Пример 4. Решите уравнение:
Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней:
Деление обеих частей уравнения на 4x, как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x.
Ответ: x = 0.
Пример 5. Решите уравнение:
Решение: функция y = 3x, стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет.
Ответ: x = -1.
Пример 6. Решите уравнение:
Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи:
![]()
Ответ: x = 2.
Решение показательных неравенств
Показательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней.
Для решения показательных неравенств требуется знание следующей теоремы:
Теорема 2. Если a > 1, то неравенство af(x) > ag(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 < a < 1, то показательное неравенство af(x) > ag(x) равносильно неравенству противоположного смысла: f(x) < g(x).
Пример 7. Решите неравенство:
Решение: представим исходное неравенство в виде:
Разделим обе части этого неравенства на 32x, при этом (в силу положительности функции y = 32x) знак неравенства не изменится:
Воспользуемся подстановкой:
Тогда неравенство примет вид:
Итак, решением неравенства является промежуток:
переходя к обратной подстановке, получаем:
Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:
Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательно получаем ответ:
Пример 8. Решите неравенство:
Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде:
Введем новую переменную:
С учетом этой подстановки неравенство принимает вид:
Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство:
Итак, неравенству удовлетворяют следующие значения переменной t:
Тогда, переходя к обратной подстановке, получаем:
Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству:
Окончательно получаем ответ:
Пример 9. Решите неравенство:
![]()
Решение:
![]()
Делим обе части неравенства на выражение:
![]()
Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем:
![Rendered by QuickLaTeX.com \[ 2\cdot\left(\frac{2}{3}\right)^{2x^2-6x+2}+\left(\frac{2}{3}\right)^{x^2-3x+1}-3\geqslant 0. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e1c87f6809ab3de421fbe72676d1d91e_l3.png)
Воспользуемся заменой переменной:
![Rendered by QuickLaTeX.com \[ t = \left(\frac{2}{3}\right)^{x^2-3x+1}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-350dbbf42f1fab4293b6b269c81ab926_l3.png)
Исходное уравнение тогда принимает вид:
![]()
Итак, неравенству удовлетворяют значения t, находящиеся в промежутке:
![]()
Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая:
![Rendered by QuickLaTeX.com \[ \left[\begin{matrix}\left(\frac{2}{3}\right)^{x^2-3x+1}\leqslant -\frac{3}{2}, \\ \left(\frac{2}{3}\right)^{x^2-3x+1}\geqslant 1\end{matrix}\right. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8090e063d15eae87eea18c1385077c24_l3.png)
Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе:
![Rendered by QuickLaTeX.com \[ \left(\frac{2}{3}\right)^{x^2-3x+1}\geqslant 1\Leftrightarrow \left(\frac{2}{3}\right)^{x^2-3x+1}\geqslant \left(\frac{2}{3}\right)^{0} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-6b98b335a32d075bae321b66303d251c_l3.png)
Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству:
![]()
Итак, окончательный ответ:
![Rendered by QuickLaTeX.com \[ x\in\left[\frac{3-\sqrt{5}}{2};\frac{3+\sqrt{5}}{2}\right]. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-70f642f908cd4359530ce2c04c6f83dd_l3.png)
Пример 10. Решите неравенство:
![]()
Решение:
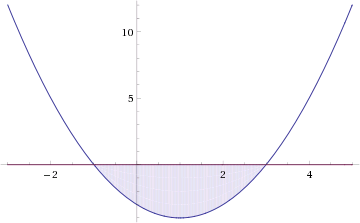
Ветви параболы y = 2x+2-x2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:
![]()
Ветви параболы y = x2-2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:
![]()
Вместе с этим ограниченной снизу оказывается и функция y = 3x2-2x+2, стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 31 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1.
Ответ: x = 1.
Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене.
Репетитор по математике в Тропарёво
Сергей Валерьевич
P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.

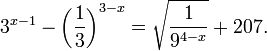
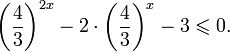
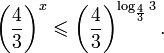
На самом деле понятно, только я все равно не могу разобраться с некоторыми уравнениями.
Спрашивайте, постараюсь объяснить.
Здравствуйте. Есть неравенство, вызывающее вопрос.
2^(x-1)>(1÷16)^(1÷x)
Надеюсь, пример понятен. Проблема в том, что когда я решаю его традиционным методом, то часть решений не подходит непонятно почему. Если можете, объясните, буду очень благодарен!
Здравствуйте, напишите, как вы его решаете традиционным способом, тогда я смогу объяснить, что и почему там не подходит.
Подскажите пожалуйста, если решаем уравнение, и в показателе модуль, рассматриваем два случая раскрытия, с плюсом и минусом? и оба числа будут являться решением?
Да, конечно. Все корни, которые получатся, будут корнями исходного показательного уравнения.
2 в степени (икс квадрат + икс по модулю) умножить на 3 в степени (- модуль икс) меньше или равно 1. Решить слабо?
Да ни разу: [0; логарифм по основанию 2 от 1.5]
не могу разобрать неравенство 2х во второй степени умнож на 49 больше 16 умножить на 7 в степени(х в квадрате минус2) помогите,пожалуйста,если сможете
извините,а как долго ждать результат?
При решении приходим к уравнению вида: 8*7^(t-4)=t, которое в элементарных функциях не решается. Так что, если это школьное задание, дальше тут обсуждать нечего, если нет — отпишитесь, можно продолжить.
Помогите решить до конца не могу разобраться
25^х + 175*5^х-2 — 60 = 0
Вообще это стандартное показательное уравнение. 25^x = (5^2)^x = (5^x)^2, 5^(x-2) = 5^x/5^2 = 5^x/25. Решается заменой переменной t = 5^x. В чем конкретно сложность возникла?
как решить?
4^х-3*6^х+9^х<0
Представить 4^x = 2^(2x), 6^x=2^x*3^x, 9^x=3^(2x) и разделить обе части уравнения на 3^(2x). Получится неравенство, которое заменой t=(2/3)^x приводится к квадратному и дальше легко решается. Посмотрите пример 7 в статье.
честно, все эти замены, уууух, какие непонятные. при попытке решать задачи по вашему примеру, учительница наорала и попросила слушать больше ее, нежели интернетовских «умников», даа, вот такая вот учительница. и вопрос:возможно ли выучить ВСЕ это, будучи при этом морковкой полной?
Могу сказать из личного опыта, что для учительницы надо решать так, как учит учительница, а на ЕГЭ или вступительном экзамене — надо решать правильно:-). А по поводу вопроса о том, можно ли всё это выучить и научиться решать, ответ — да, если действительно перед собой такую цель поставить. И можно при этом быть хоть морковкой, хоть Чипполиной.
Пример 1. Решите уравнение:
2^{2x+1}-5*2^x-88=0.
Простите, почему Вы раскрываете это уравнение как
2t^2-5t+88=0 ?
Первая часть раскроется как 4t^2, в скобке ведь два слагаемых — то есть 2^2x * 2, разве нет?
Правильно:. 2*2:(2x). Если ввести подстановку t=2^x, то как раз 2*t^2 и получатся. Откуда там четверке взяться?
О, точно, спасибо.
На лишнюю двойку умножил
3^x²-7.2x>1/3×9^1/5 как решить неравенство. Бред у меня получается
Имеется ввиду это неравенство: http://www.wolframalpha.com/input/?i=3%5E%28x%5E2%29-7.2*x%3E1%2F3%C3%979%5E%281%2F5%29
Или какое-то другое?
Очень информативная статья у вас! Благодарю)
На свой примерчик только ничего не нашла, помогите пожалуйста решить уравнение :
(2-√3)^x+(2+√3)^x — 2 = 0
Рад что Вам понравилась статья. По поводу Вашего примера:
здесь нужно воспользоваться тем, что (2-√3)(2+√3) = 1. То есть (2-√3) = 1/(2+√3). Тогда уравнение принимает вид: 1/(2+√3)^x+(2+√3)^x — 2 = 0. Далее замена: (2+√3)^x = t, t>0. t+1/t-2 = 0, t^2-2t+1 = 0, t = 1. Обратная замена (2+√3)^x = 0, откуда x = 0.
Сергей, спасибо большое за статью. очень помогла. а вот с одним не разобралась. если не трудно, посмотрите. 2 в степени х^2 умножить на 3^х равно 6. один корень равен 1, а другой?
Здравствуйте, рад, что статья оказалась для Вас полезной. По поводу примера. Разделим обе части уравнения на 6, получится 2^(x^2-1)*3^(x-1) = 1, теперь разделим обе части на 3^(x-1) и представим (x^2-1) = (x-1)(x+1), тогда получим: (2^(x+1))^(x-1) = (1/3)^(x-1). Берем логарифм на основанию 2 из обоих частей, тогда получим: (x-1)(x+1) = (x-1)log_2(1/3) или (x-1)(x+1-log_2(1/3))=0, откуда x1 = 1, x2 = log_2(1/3)-1.
благодарю за помощь))) очень тронута.
Всегда пожалуйста, обращайтесь:-)
многое забывается, если долго не заниматься. приходится сейчас наверстывать свои упущения. еще одно задание решала долго. пробовала разными способами получается только один корень, а нужно найти сумму корней. может опечатка ? 9*16^х-7*12^х-16*9^х=0
Да, это правда, если долго не заниматься, все забывается со временем. Это уравнение нужно представить в виде 9*4^(2х)-7*3^х*4^x-16*3^(2х)=0 и поделить обе части на 3^(2x). Тогда получится 9*(4/3)^(2x)-7*(4/3)^x-16 = 0. Дальше замена (4/3)^x = t. То есть 9t^2-7t-16=0, откуда t1 = -1, t2 = 16/9. Обратная замена: (4/3)^x = -1, (4/3)^x = 16/9, x = 2, а в первом, действительно, корней нет. Значит надо писать в ответ 2.
Добрый день! Помогите , пожалуйста, решить неравенство.
2^((1-х)/(3+х))*7^(х+3)=56
Вместо = знак >=
Так как 56 = 2^3*7, то неравенство можно привести к виду: (2^(-4/(3+x)))^(x+2)>=(1/7)^(x+2). Откуда (x+2)*(-4/(3+x)+log_2(7))>=0. Решая методом интервалов, получаем: (-3;-2] U [(4-3*log_2(7))/log_2(7);+∞)
Помогите, пожалуйста, решить неравенство:
4х^4 +2х^3 -8х^2 +х+1 <=0
Если можете, то с подробным решением
Выражение 4х^4 +2х^3 -8х^2 +х+1 можно представить в виде: (x-1)(x-1/2)(x^2+2x+1/2). Как это делать, смотрите в этом видео: https://www.youtube.com/watch?v=neqaS55NJOA. Ну а дальше стандартный метод интервалов (подробнее здесь: https://www.youtube.com/watch?v=d1PGcy-sLl0). Ответ получится: [(-2-корень(2))/2;(-2+корень(2))/2] в объединении с [1/2;2].
Помогите решить
3 в степени (2х минус 6) = 9 в степени (2√х)
Все нужно привести к основанию 3. Получается 3^(2x-6) = 3^(4√х). Откуда 2x-6 = 4√х. Из чего получаем окончательно x = 9.
как решать с модулем, можете объяснить пожалуйста
На эту тему есть специальная статья на сайте: уравнения и неравенства с модулем
помогите решить показательное уравнение. Калькулятор только дает ответ, а мне нужно решение 4*4^x+(4*x-13)*2^x+3-x=0
Берём подстановку 2^x=t, тогда получаем квадратное уравнение 4*t^2+(4*x-13)*t+3-x=0 относительно t с дискриминантом (4x-11)^2. Тогда корни t1 = (13-4x+|4x-11|)/8 или t2=(13-4x-|4x-11|)/8. Дальше обратная постановка, потом корни.
не могу понять как решать уравнения с одинаковым корне
пример:3^x<5^x
Делим обе части на 3^x>0. Получаем (5/3)^x>1 или (5/3)^x>(5/3)^0. То есть x>0.
дано: 5^(х+2)+5^(х+1)-5^х<3^(х/2+1)-3^(х/2)-3^(х/2-1) получил 29*5^х<5/3*3^(х/2), потом… помогите
Дальше можно представить 3^(x/2) в виде (корень(3))^x, после чего делить обе части неравенства на положительное выражение (корень(3))^x. Цель: представить неравенство в таком виде, чтобы с одной стороны была показательная функция (тут получится возрастающая), а с другой — число.
Помогите, пожалуйста, решить уравнение:
(3-sqrt(8))^(x/3) + (3+sqrt(8))^(x/3) =2.5
Домножаю на сопряженное первое слагаемое, делаю подстановку, решаю квадратное уравнение, получаются какие-то неудобные корни, обратная подстановка и логарифмирование ничего хорошего не дает. Как же его решать, это уравнение?! Заранее благодарна.
Здесь нужно использовать то, что (3-sqrt(8))*(3+sqrt(8)) = 1. То есть нужно заменить 3+sqrt(8) на 1/(3-sqrt(8)) и сделать удобную подстановку. Хороших корней здесь не получится, но иррациональные числа ничем не хуже других.
Нашла ошибку, все получилось, извините за беспокойство.
Решила сама.
Уважаемые гости! Пожалуйста, не пишите сюда заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
мне нужно построить график функции y=(1/3) в степени х, минус 3. Если тупо подставлять в уравнение значения х, получается что-то не то. Построила два графика один y=(1/3) в степени х, второй у=-3. Правильно ли это?
Здравствуйте. Помогите пожалуйста решить уравнение 2^(x-1)>(1÷16)^(1÷x)
Буду очень благодарен! Заранее спасибо
пожалуйста помогите как решать эту уравнению; 2^(a+4)= 6; 3^(2b+1)=12 . 3^(ba-2) =?
Спасибо! Очень полезная информация.
Помогите пожалуйста решить! 0,5^х+7 * 0,51-2х=2
Решите пожалуйста эту задачу
Два в степени икс ровно шесть минус икс
И так же
(½) в степени икс=x+6
Спасибо большое!!!!! Очень помогло разобраться в этом во всем, СПАСИБО))))
6^x-3-2^x-0,5*3^x+1,5=0
решите пожалуйста
У меня вопрос по первому примеру, куда делась единица? То есть: 2^(2x+1)-5*2^x-88=0, при подстановке в t=2x, по идее, должно получиться 2t^(2+1)-5t-88=0, разве не так?