Данная статья посвящена разбору решенией неравенств (логарифмических и неравенств с модулем) методом рационализации. Данный метод становится в последнее время всё более популярным, поскольку помогает существенно упростить решение неравенств, которые встречаются во второй части профильного ЕГЭ по математике. Так что, если вы готовитесь к сдаче этого экзамена и не знакомы с решением неравенств методом рационализации, данная статья может оказаться для вас чрезвычайно полезной.
«Стандартный» метод решения логарифмических неравенств
Рассмотрим традиционный метод решения логарифмического неравенства на конкретном примере.
| Пример 1. Решить логарифмическое неравенство:
|
Вне зависимости от того, каким методом вы решаете то или иное логарифмическое неравенство, начинать всегда нужно с области допустимых значений. Основание логарифма должно быть положительным и не равным 1, а выражение, стоящее под знаком логарифма, — положительным. То есть область допустимых значений в нашем примере определяется следующей системой:
![Rendered by QuickLaTeX.com \[ \begin{cases} x>0,\, x\ne 1 \\ x+2>0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e7c22a4ea36d5032b68e7489b0a67a45_l3.png)
Легко видеть, что решением данной системы является промежуток: ![]() .
.
Теперь, используя свойства логарифмов, представим двойку справа в виде логарифма с основанием ![]() . Тогда неравенства примет вид:
. Тогда неравенства примет вид:
![]()
Далее решение неравенства разбивается на два случая:
1) если ![]() . В этом случае в основаниях логарифмов стоят одинаковые числа из интервала
. В этом случае в основаниях логарифмов стоят одинаковые числа из интервала ![]() . Значит, соответствующие логарифмические функции являются убывающими. Поэтому, опуская знаки логарифмов, нам нужно изменить знак неравенства на обратный. В результате в этом случае приходим к следующему неравенству:
. Значит, соответствующие логарифмические функции являются убывающими. Поэтому, опуская знаки логарифмов, нам нужно изменить знак неравенства на обратный. В результате в этом случае приходим к следующему неравенству:
![]()
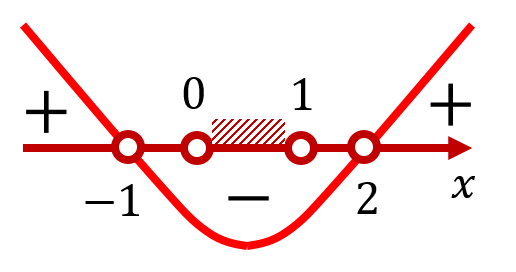
Изобразим соответствующую параболу, ветви которой направлены вверх, пересекающую ось OX в двух точках: ![]() и
и ![]() , являющихся корнями квадратного трёхчлена
, являющихся корнями квадратного трёхчлена ![]() :
:
Тогда с учётом рассматриваемого ограничения на ![]() получаем для этого случая
получаем для этого случая ![]() .
.
2) рассмотрим теперь случай, когда ![]() . В этом случае оба логарифма будут возрастающими, поэтому после ухода от знаков логарифма, знак неравенства останется прежним. То есть в этом случае исходное логарифмическое неравенство можно заменить следующим:
. В этом случае оба логарифма будут возрастающими, поэтому после ухода от знаков логарифма, знак неравенства останется прежним. То есть в этом случае исходное логарифмическое неравенство можно заменить следующим:
![]()
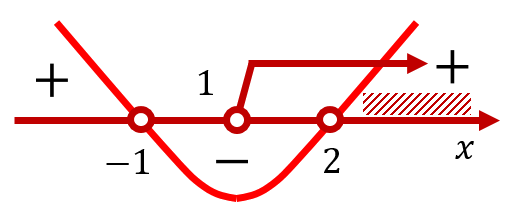
В учётом ограничения на ![]() решение этого неравенства можно проиллюстрировать на числовой прямой следующим образом:
решение этого неравенства можно проиллюстрировать на числовой прямой следующим образом:
То есть решение в данном случае имеет вид: ![]() .
.
Объединяя решения, полученные в пунктах а) и б), приходим к окончательному ответу, который имеет вид: ![]() .
.
Решение логарифмических неравенств методом рационализации
Описанный в предыдущем параграфе способ является правильным, но при этом чрезвычайно неудобным. Как видите, приходится рассматривать два отдельных случая, что существенно повышает вероятность совершения ошибки. Гораздо проще поступить следующим образом. Перепишем исходное логарифмическое неравенства в виде:
![]()
А дальше, в области допустимых значений, то есть при ![]() (это мы установили выше), данное неравенство можно заменить следующим равносильным ему неравенством:
(это мы установили выше), данное неравенство можно заменить следующим равносильным ему неравенством:
![]()
Ну действительно, если ![]() , то первая скобка положительна, и на неё можно разделить, не меняя при этом знак неравенства. Если же
, то первая скобка положительна, и на неё можно разделить, не меняя при этом знак неравенства. Если же ![]() , то первая скобка отрицательна, и при делении на неё, знак неравенства изменится на противоположный.
, то первая скобка отрицательна, и при делении на неё, знак неравенства изменится на противоположный.
То есть мы получили ровно то же самое, что имели в предыдущем пункте. Но при этом нет необходимости рассматривать два случая. Всё решается в рамках одного единственного неравенства. И хотя этот способ не избавляет нас от необходимости определения области допустимых значений, он всё равно приводит к существенному упрощению решения задачи.
Решаем полученное неравенство методом интервалов. Для этого поменяем знаки во второй скобке, разделим обе части неравенства на -1, поменяв знак неравенства:
![]()
Теперь разложим выражение во вторых скобках на множители:
![]()
Изобразим на числовой прямой множество решений полученного неравенства (стрелкой обозначена область допустимых значений исходного логарифмического неравенства):
В результате получаем тот же результат, что и в предыдущем параграфе:
![]() .
.
Итак, метод рационализации логарифмических неравенств состоит в следующем.
![]()
в области его допустимых значений можно заменить равносильным неравенством
![]()
Здесь знак ![]() означает любой из знаков
означает любой из знаков ![]() ,
, ![]() ,
, ![]() или
или ![]() .
.
| Пример 2. Решите неравенство:
|
Область допустимых значений данного неравенства определяется следующей системой неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} 0.25x^2>0 \\ 0.25x^2\ne 1 \\ \frac{x+6}{4}>0 \end{cases}\Leftrightarrow \begin{cases} x\ne 0 \\ x\ne 2,\, x\ne -2 \\ x>-6. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1172b9fae646018e22e73d9a6e17bd12_l3.png)
Итак, область допустимых значений задаётся следующим промежутком:
![]() .
.
Представим единицу справа в виде логарифма с основанием ![]() и перенесём его в левую сторону неравенства:
и перенесём его в левую сторону неравенства:
![]()
Воспользуемся методом рационализации. В области допустимых значений данное неравенство можно заменить следующим:
![]()
Умножим обе части на -4, поменяв при этом знак неравенства:
![]()
Разложим на множители выражение, стоящее в обеих скобках:
![]()
Если умножить обе части на 2 и внести этот множитель во вторую скобку, то получится следующее уравнение:
![]()
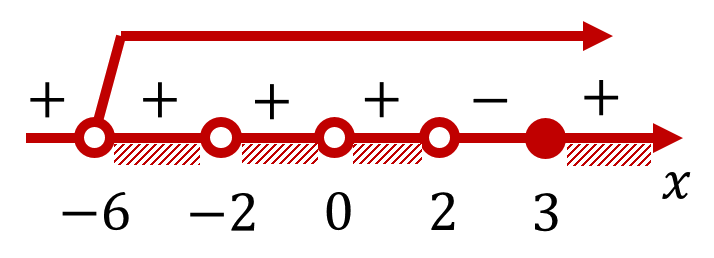
Изобразим на числовой прямой промежутки, на которые разбивают числовую ось корни полученного многочлена слева, определим знаки многочлена в каждом промежутке и выделим решение неравенства с учётом области допустимых значений:
Итак, окончательный ответ:
![]() .
.
Решение неравенств с модулем методом рационализации
Метод рационализации не ограничивается, конечно, возможностью решения лишь логарифмических неравенств. Вообще, суть метода в том, чтобы заменить «неудобные» части в выражении более простыми, которые имеют такой же знак, что и исходные части при тех же значениях ![]() . Поэтому метод рационализации применим к множеству различных неравенств. В том числе, к неравенствам с модулями.
. Поэтому метод рационализации применим к множеству различных неравенств. В том числе, к неравенствам с модулями.
К решению любого неравенства с модулем можно подойти стандартным образом. Раскрывать модули в зависимости от знаков подмодульных выражений при различных значениях ![]() . Однако, можно воспользоваться следующим свойством.
. Однако, можно воспользоваться следующим свойством.
Знак выражения ![]() совпадает со знаком выражения
совпадает со знаком выражения ![]() при любых значениях
при любых значениях ![]() . Это и используется при решении неравенств с модулями методом рационализации.
. Это и используется при решении неравенств с модулями методом рационализации.
![]()
равносильно неравенству
![]()
Здесь знак ![]() означает любой из знаков
означает любой из знаков ![]() ,
, ![]() ,
, ![]() или
или ![]() .
.
Ну действительно, известно, что ![]() и
и ![]() . Тогда обе части неравенства можно возвести в квадрат, перенести всё в одну сторону и воспользоваться формулой «разность квадратов»:
. Тогда обе части неравенства можно возвести в квадрат, перенести всё в одну сторону и воспользоваться формулой «разность квадратов»:
![]()
![]()
![]()
В этом и состоит суть метода рационализации неравенств, содержащих модули. Рассмотрим конкретный пример.
| Пример 3. Решите неравенство:
|
Воспользуемся методом рационализации для решения данного неравенства. Заменим его равносильным и более простым неравенством:
![]()
![]()
Приведём подобные слагаемые в обеих скобках:
![]()
Из первой скобки вынесем множитель -10, а из второй — множитель ![]() и разделим обе части неравенства на -20, поменяв при этом его знак:
и разделим обе части неравенства на -20, поменяв при этом его знак:
![]()
Видно, что выражение слева может быть меньше нуля только при ![]() (так как второй множитель всегда неотрицателен, ибо является полным квадратом), а равно нулю при
(так как второй множитель всегда неотрицателен, ибо является полным квадратом), а равно нулю при ![]() или
или ![]() . Итак, окончательный ответ к данному неравенству:
. Итак, окончательный ответ к данному неравенству:
![]() .
.
Вот такое простое и изящное решение. При этом можете себе представить, что было бы, если бы мы решили воспользоваться стандартным методом решения неравенств с модулями и стали бы раскрывать модули при различных значениях ![]() .
.
Рассмотрим ещё один пример решения неравенства с модулем методом рационализации. На этот раз из реального прототипа заданий для ЕГЭ по математике.
| Пример 4. Найдите все значения выполняется при всех |
Воспользуемся методом рационализации для решения данного неравенства с модулем. Заменим исходное неравенство равносильным ему неравенством без модулей:
![Rendered by QuickLaTeX.com \[ \left(\frac{x^2+ax+1}{x^2+x+1}-3\right)\left(\frac{x^2+ax+1}{x^2+x+1}+3\right)<0. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f1fe1f0e6b58ecf75123d087e0980a97_l3.png)
После преобразования выражений, находящихся в скобках, получаем следующий результат:
![]()
Поскольку ![]() при всех значениях
при всех значениях ![]() , то можно дважды умножить обе части полученного неравенства на
, то можно дважды умножить обе части полученного неравенства на ![]() , не меняя при этом знак неравенства. В результате приходим к следующему неравенству:
, не меняя при этом знак неравенства. В результате приходим к следующему неравенству:
![]()
Или после умножения обеих частей на -1:
![]()
Последнее неравенство может быть выполнено для любых ![]() только в том случае, если обе соответствующие параболы, ветви которых направлены вверх, целиком лежат выше оси OX. Это условие выполняется в том случае, если дискриминанты обоих квадратных трёхчленов отрицательны. То есть имеет место система неравенств:
только в том случае, если обе соответствующие параболы, ветви которых направлены вверх, целиком лежат выше оси OX. Это условие выполняется в том случае, если дискриминанты обоих квадратных трёхчленов отрицательны. То есть имеет место система неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} (a-3)^2-16<0 \\ (a+3)^2-64<0. \end{cases}\Leftrightarrow \begin{cases} (a-3)^2<16 \\ (a+3)^2<64. \end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-efc8827a9daefde7d40388c3f76d9f1a_l3.png)
![Rendered by QuickLaTeX.com \[ \Leftrightarrow \begin{cases} -4<a-3<4 \\ -8<a+3<8. \end{cases}\Leftrightarrow \begin{cases} -1<a<7 \\ -11<a<5. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-35d509efbf7197ab022c7bd2be93020e_l3.png)
Решением этой системы является промежуток: ![]()
Примечание. Предвижу ваши возражения. Да, неравенство типа ![]() можно сразу заменить двойным неравенством
можно сразу заменить двойным неравенством ![]() . Здесь просто для иллюстрации предложен альтернативный способ решения неравенства методом рационализации.
. Здесь просто для иллюстрации предложен альтернативный способ решения неравенства методом рационализации.
На самом деле предложенный метод, конечно, работает не только с неравенствами, но и с уравнениями. Рассмотрим для примера решение следующего примера из реальных прототипов заданий ЕГЭ по математике.
| Пример 5. Найдите все значения имеет более двух различных корней. |
Заменим данное уравнение следующим равносильным ему уравнением:
![]()
![]()
Или после упрощения выражений, стоящих в обеих скобках:
![]()
![]()
После вынесения общих множителей из скобок получаем:
![]()
Заметим, что при ![]() корень
корень ![]() может быть любым числом. Этот случай нам подходит. Для
может быть любым числом. Этот случай нам подходит. Для ![]() разделим обе части этот уравнения на
разделим обе части этот уравнения на ![]() :
:
![]()
Данное уравнение может иметь от 1 до 3 корней. Нам нужны случаи, когда будет 3 различных корня. Один из этих корней обязательно будет равен ![]() . Следовательно, задача сводится к поиску всех значений параметра
. Следовательно, задача сводится к поиску всех значений параметра ![]() , при каждом из которых квадратный трёхчлен, стоящий в скобках имеет два корня, каждый из которых отличен
, при каждом из которых квадратный трёхчлен, стоящий в скобках имеет два корня, каждый из которых отличен ![]() . Это условие достигается тогда и только тогда, когда дискриминант этого квадратного трехчлена положителен и значение многочлена в скобках при
. Это условие достигается тогда и только тогда, когда дискриминант этого квадратного трехчлена положителен и значение многочлена в скобках при ![]() не равно нулю. То есть имеет место система неравенств:
не равно нулю. То есть имеет место система неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} (1-a)^2-4(4 - 3a)>0 \\ 3^2-3(a-1)+4 - 3a\ne 0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-22d764468340a0ded3b1e305d0826df0_l3.png)
Эту систему можно упростить:
![Rendered by QuickLaTeX.com \[ \begin{cases} a^2+10a-15>0 \\ 8-3a\ne 0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2c669c9253e3fe851dcb06bc84ab0878_l3.png)
Решением этой системы является промежуток:
![]() .
.
Домашнее задание по решению неравенств методом рационализации
Итак, из этой статьи вы узнали, в чем состоит суть метода рационализации и научились применять его при решении логарифмических неравенств, а также неравенств, содержащих модули. Для того, чтобы закрепить полученные знания, предлагаю вам решить самостоятельно следующие неравенства:
(1) ![]()
(2) ![]()
Пишите свои варианты ответов и решений в комментариях. Успехов!
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич


![Rendered by QuickLaTeX.com \[ \left|\frac{x^2+ax+1}{x^2+x+1}\right|<3 \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c8d94da927b529311fa0cd4cf16b336a_l3.png)
Трубы готовы. Можете забрать.
почему в егэ 2018 профиль по математике фипи в разобранном примере вариант 27 в задании
15 пишут при решении методом рац онализации (f(x)-1) в степени -1
Нужно увидеть этот разобранный пример, чтобы ответить.
Думаю, что у них опечатка. С какой радости там -1 степень?!!!
в самом конце подставляем -3, тогда 9+3а-3+4-3а не равно 0, 10 не равно 0 при любых а. или я что-то пропустила?
Корень x=3, а не -3, там опечатка была, исправил, спасибо!
Непонятно, почему а = -1 не подходит. Нам же необходимо, чтобы корней было более двух! А здесь подходит любое. Это уж точно больше двух))))
Спасибо за Ваше замечание, -1, конечно, подходит. Исправил.
Получилось 7/3, а не 8/3. Что то не то
Уже разобралась
Спасибо!
(1) Ответ: (-1;0) u (0;1/2] u (1;+~)
(2) Ответ: {4} u [4;+~)
Виноват
Во втором ответ : {1} u [4;+~)
со вторым согласен, а в первом по-моему не правильно, у меня получилось (1;+~)
В первом дз ответ: [2;+~]?
Не?
Нет, выше написан правильный ответ к первому.
Спасибо за статью! Мне оказалось очень полезно. Единственный вопрос, на который я никак не найду ответа: как самой научиться выводить рационализацию? то есть, как в каждом случае понять, на что можно заменить. Ну не зазубривать же все случаи
Нужно просто всегда заменять на такие рациональные выражения, которые имеют те же знаки на всех промежутках, что и у исходного выражения.
Спасибо