Со школы нас учат, что уравнение ![]() не имеет решений, ибо синус не может принимать значений, которые больше 1. Однако, всё это ложь! Настало время рассказать правду. У этого уравнения есть решение в комплексных числах! Дочитайте эту статью до конца, и вы узнаете, как на самом деле решается уравнение sin(x)=2.
не имеет решений, ибо синус не может принимать значений, которые больше 1. Однако, всё это ложь! Настало время рассказать правду. У этого уравнения есть решение в комплексных числах! Дочитайте эту статью до конца, и вы узнаете, как на самом деле решается уравнение sin(x)=2.
Какие бывают числа
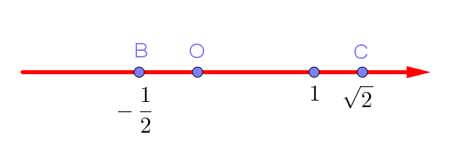
Со школы вам рассказывают, что числа можно расположить на прямой. Для неё даже придумали специальное название — «числовая прямая». То есть прямая, на которой отмечена точка O (начало отсчёта), положительное направление (обычно вправо) и масштаб, задающий положение точек, соответствующих различным числам. И действительно, на такой числовой прямой можно отмечать различные числа: целые, дробные и даже иррациональные:
Вся школьная математика сосредоточена на изучении только тех чисел, которые могут быть изображены на этой прямой. В буквальном смысле школьные учителя заставляют нас ползать по этой прямой туда и обратно, зачастую не давая осознать, что реальная картина чисел намного более многогранна.
На числовой прямой могут быть изображены только действительные числа (рациональные и иррациональные). Однако, если выбраться за рамки этой прямой и оказаться в плоскости, то мы столкнёмся с огромным множеством ранее неизвестных нам комплексных чисел. Для наглядного отображения таких чисел используется так называемая комплексная плоскость.
Что такое комплексная плоскость
Она задаётся двумя взаимно перпендикулярными осями, которые по традиции называются «действительной» (Re-ось) и «мнимой» (Im-ось). Стоит отметить, что термин «мнимый» не отражает настоящей сути и является лишь данью уважения традициям. На самом деле комплексные числа не чуть не менее «естественны», чем все остальные.
Любое комплексное число ![]() может быть представлено в виде:
может быть представлено в виде:
![]()
где ![]() и
и ![]() — действительные (вещественные) числа, а
— действительные (вещественные) числа, а ![]() — так называемая «мнимая единица», то есть число, квадрат которого равен -1. То есть:
— так называемая «мнимая единица», то есть число, квадрат которого равен -1. То есть:
![]()
С первого взгляда это кажется немыслимым, ведь квадрат числа не может быть отрицательным. Оказывается, что может, если это число комплексное. И использование такого подхода позволяет получить огромное количество новых возможностей.
Так вот, вдоль «действительной» оси на комплексной плоскости откладываются действительные (вещественные) числа. Фактически, эта ось представляет собой нашу любимую числовую прямую. Вдоль «мнимой» оси откладываются чисто комплексные числа, вроде ![]() ,
, ![]() ,
, ![]() и т.д. Используя такой подход, каждому комплексному числу удаётся поставить в соответствие единственную точку на комплексной плоскости.
и т.д. Используя такой подход, каждому комплексному числу удаётся поставить в соответствие единственную точку на комплексной плоскости.
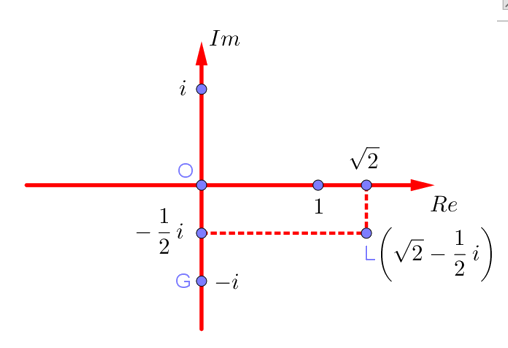
Например, таким образом отмечается точка на комплексной плоскости, соответствующая комплексному числу ![]() (точка L):
(точка L):
Однако, есть ещё один способ представления комплексных чисел, который нам нужно рассмотреть, прежде чем перейти к решению уравнения. Дело в том, что положение любой точки на комплексной плоскости можно задать с помощью радиус-вектора ![]() , проведённого из точки O. Тогда длину этого радиус-вектора
, проведённого из точки O. Тогда длину этого радиус-вектора ![]() называют модулем комплексного числа, а угол
называют модулем комплексного числа, а угол ![]() между этим вектором и положительным направлением Re-оси — аргументом комплексного числа.
между этим вектором и положительным направлением Re-оси — аргументом комплексного числа.
В качестве иллюстрации изобразим на комплексной плоскости точку, соответствующую комплексному числу ![]() . Тогда из вполне очевидных геометрических соображений получим, что модуль этого числа равен
. Тогда из вполне очевидных геометрических соображений получим, что модуль этого числа равен ![]() , а аргумент, соответственно,
, а аргумент, соответственно, ![]() :
:
Тогда из чисто тригонометрических соображений можно сказать, что число ![]() может быть представлено также в следующем виде:
может быть представлено также в следующем виде:
![]()
И вообще, любое комплексное число ![]() может быть представлено в виде:
может быть представлено в виде:
![]()
где ![]() и
и ![]() .
.
Надо сказать, что такое представление является неоднозначным, ибо определено для аргумента с точностью до целого числа полных оборотов радиус-вектора вокруг точки O, То есть, строго говоря, одному и тому же комплексному числу соответствует бесконечно много тригонометрических представлений типа:
![]()
Этот момент нужно запомнить, поскольку он понадобится нам в дальнейшем при решении уравнения.
И последний важнейший момент, который нам нужно обсудить, связан с именем одного из величайших математиков всех времён Леонердом Эйлером. Именно ему принадлежит честь введения формулы:
![]()
Благодаря использованию этой формулы мы может перейти к так называемому показательному представлению комплексного числа, которое мы также будем активно использовать при решение нашего уравнения:
![]()
Излишне уточнять, что показательное представление также справедливо для каждого комплексного числа с точностью до целого количества полных оборотов радиус-вектора вокруг точки O. Например, для числа ![]() имеем:
имеем:
![]()
Решение уравнение sin(x) = 2
Запишем дважды уравнение Эйлера для аргументов ![]() и
и ![]() :
:
(1) ![]()
![]()
Последнее уравнение из-за чётности косинуса и нечётности синуса можно переписать в виде:
(2) ![]()
Складываем почленно уравнения (1) и (2), после чего выражаем ![]() :
:
![]()
Итак, требуется решить уравнение:
![]()
Введём замену ![]() . И хотя при комплексных аргументах
. И хотя при комплексных аргументах ![]() может принимать отрицательные значения, нулю это выражение равно быть не может. То есть мы хотя бы уверены в том, что
может принимать отрицательные значения, нулю это выражение равно быть не может. То есть мы хотя бы уверены в том, что ![]() . Тогда после замены уравнение принимает вид:
. Тогда после замены уравнение принимает вид:
![]()
Дробь равна нулю, когда нулю равен её числитель, а знаменатель не равен нулю (это условие, как мы уже выяснили, выполнено). Итак, решаем уравнение:
![]()
Дискриминант этого квадратного уравнения равен:
![]()
Тогда корнями являются числа ![]() . Решение этого квадратного уравнения во всех подробностях рассмотрено в прилагающемся видеоролике.
. Решение этого квадратного уравнения во всех подробностях рассмотрено в прилагающемся видеоролике.
Отлично, настало время вернуться к исходной переменной. Делаем обратную подстановку:
![]()
Осталось выразить из этого уравнения ![]() , и это будет ответ. Как же нам это сделать? Нужно взять натуральный логарифм от обеих частей:
, и это будет ответ. Как же нам это сделать? Нужно взять натуральный логарифм от обеих частей:
![]()
Или по-другому:
![]()
И здесь есть один тонкий момент, который нужно принять во внимание. Дело в том, что в комплексных числах возможны логарифмы как от положительных, так и от отрицательных чисел. Логарифма нуля, к счастью, не существует. Но что ещё более интересно, логарифмы в комплексных числах принимают бесконечное множество значений из-за того, что, как мы уже говорили, показательное представление комплексных чисел неоднозначно (верно в точностью до целого числа ![]() , добавляемого или отнятого из аргумента комплексного числа).
, добавляемого или отнятого из аргумента комплексного числа).
Именно поэтому при вычислении натурального логарифма слева в полученном уравнении мы получаем не одно единственное значение ![]() , а бесконечное множество значений
, а бесконечное множество значений ![]() :
:
![]()
Осталось ответить на ещё один интересный вопрос, и наша задача будет решена. Чему же равен ![]() ? Для ответа на этот вопрос нам нужно вернуться на комплексную плоскости и постараться представить комплексное число
? Для ответа на этот вопрос нам нужно вернуться на комплексную плоскости и постараться представить комплексное число ![]() в показательном виде:
в показательном виде:
Из рисунка видно, что мнимую единицу ![]() можно представить в показательном виде следующим образом:
можно представить в показательном виде следующим образом:
![]()
Тогда наше выражение принимает вид:
![]()
Ну и тогда, с учётом сказанного вше относительно многозначности логарифма в компексных числах, получаем следующий результат:
![]()
После деления обеих частей этого равенства на ![]() и преобразования полученного выражения получаем окончательный ответ:
и преобразования полученного выражения получаем окончательный ответ:
![]()
Вот такое решение на самом деле имеет уравнение sin(x) = 2. А не пустое множество, как вам говорили на протяжении многих лет обучения в школе. Решений не будет только в действительных числах! Но не в комплексных! Теперь вы знаете правду. Но помните, что это знание подразумевает и большую ответственность. Всего вам доброго!


Пожалуйста, переведи ответ в комплексное число!
Ответ представлен в виде серии комплексных чисел, там i — мнимая единица.
Темная магия
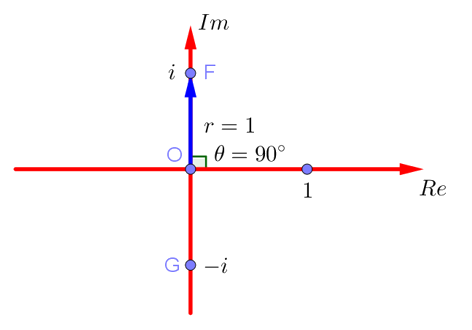
Почему решение уравнения sin(Z)=2 ищем при r=1,?
Потому что мы представляем мнимую единицу в показательной форме, а длина радиус-вектора, соответствующего точке, изображающей число i на комплексной плоскости, равна 1.
Очень понравилось! Большое спасибо. Понятно и интересно
Как представить данный в ответе угол геометрически? Например угол пи/2 понятно, что это прямой угол.
Спасибо что написали. Сам бы не разобрался.
В данном случае можно вынести знак плюс-минус из логарифма => x= pi/2 +- i*ln(2 + корень 3).
@azmt: это не угол, а пара сопряженных комплексных чисел с координатами (pi/2, ln(2 + корень 3)) и (pi/2, минус ln(2 + корень 3)).
Ну и естественно с периодом 2 pi…
Так что тов. полковник из известного анекдота про то, что «в военное время синус может достигать 4» на самом то деле высокообразованный человек :))) .
А смеющиеся над ним жалкие неучи. ЛОЛ.
Тов. полковнику всегда виднее:))
Прочитал все до конца, а в голове играла сцена из «Тот самый Мюнхгаузен» где Рамкопф доказывал что можно потянуть себя за волосы
Неочевидное доказательство
Как-то хитро, тета, определенное как реальное число вдруг заменяется на комплексное число, без даже намека на то что такая замена верна.
А верна она или нет, мы не знаем, потому что мы не знаем как ведет себя синус в комплексной области