Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.
Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.
| Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φin (внутренней) и φex (внешней). |
Решение. Потенциал на поверхности внутренней сферы φex складывается из двух потенциалов: внешней сферы φ1 и собственно внутренней сферы φ2.
Потенциал внешней сферы φ1 в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):
![\[ \varphi_1 = \frac{Q}{4\pi\varepsilon_0 R}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1cc3e42840a1850c7484a3a4373de127_l3.png "Rendered by QuickLaTeX.com")
Потенциал внутренней сферы φ2 определяется известным соотношением:
![\[ \varphi_2 = \frac{q}{4\pi\varepsilon_0 r}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2a4e163cfb1d96f29b12a6f3848bfcff_l3.png "Rendered by QuickLaTeX.com")
Тогда общий потенциал φin на поверхности внутренней сферы равен:
![\[ \varphi_{in} = \varphi_1 + \varphi_2 = \frac{1}{4\pi\varepsilon_0}\left(\frac{Q}{R}+\frac{q}{r}\right). \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1caf942b30112b91e3d1fba418e44b81_l3.png "Rendered by QuickLaTeX.com")
Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’1 и собственно внешней сферы φ’2.
Потенциал внутренней сферы φ’1 на расстоянии R от ее центра определяется известным соотношением:
![\[ \varphi'_1 = \frac{q}{4\pi\varepsilon_0 R}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-97fb05e32d3635ae941a30dd3cc4a23e_l3.png "Rendered by QuickLaTeX.com")
Формула, определяющая потенциал внешней сферы φ’2 на ее поверхности, также хорошо известна:
![\[ \varphi'_2 = \frac{Q}{4\pi\varepsilon_0 R}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7c067144f5a30cfb61a06c7698c65ecf_l3.png "Rendered by QuickLaTeX.com")
Тогда общий потенциал на поверхности внешней сферы равен:
![\[ \varphi_{ex} = \varphi'_1 + \varphi'_2 = \frac{q+Q}{4\pi\epsilon_0 R}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ffad4e6da3e93f709961a0a0e1294d13_l3.png "Rendered by QuickLaTeX.com")
| Задача 2. Металлический шар радиуса R1, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R2. Определите потенциал шара φ1 после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают. |
Решение. До соединения сфер проводником заряд первой был равен:
![\[ q=\frac{\varphi R_1}{k}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c399a8b59061b66a4ead4e0401c5a777_l3.png "Rendered by QuickLaTeX.com")
После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:
![\[ \varphi_1 = k\frac{q_1+q_2}{R_2}, \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7116bb2d886c119b3ea788263f7354c1_l3.png "Rendered by QuickLaTeX.com")
где q1 и q2 — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q1 + q2. После несложных преобразований получаем:
![\[ \varphi_1 = k\frac{q}{R_2} = \varphi\frac{R_1}{R_2}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-183106242d5846f609671777351af0f7_l3.png "Rendered by QuickLaTeX.com")
| Задача 3. Металлический шар радиуса R1, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R2. Чему станет равен потенциал шара φ‘, если заземлить оболочку? |
Начнем с рисунка к решению задачи:
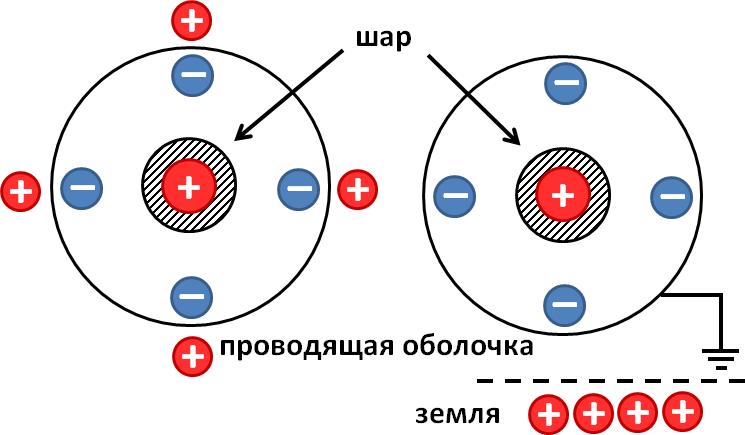
После заземления проводящей оболочки весь положительный заряд, образовавшийся на ней вследствие явления электростатической индукции, стекает на землю. На ней остается только отрицательный заряд, поскольку он притягивается к положительному заряду внутренней сферы
Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:
![\[ q = \frac{\varphi R_1}{k}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-0f14eda9fa0d7480b8defcd7c4b463ac_l3.png "Rendered by QuickLaTeX.com")
Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.
В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q2, поскольку он притягивается к положительному заряду q1 внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:
![\[ k\frac{q_1+q_2}{R_2} = 0\Leftrightarrow q_1 = q = - q_2. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8dae6728fabcc876738722f3411809ec_l3.png "Rendered by QuickLaTeX.com")
Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:
![\[ \varphi' = k\left(\frac{q_1}{R_1}+\frac{q_2}{R_2}\right) = \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3d37c928cb9f3236d57266e96173fd95_l3.png "Rendered by QuickLaTeX.com")
![\[ = k\left(\frac{q}{R_1}-\frac{q}{R_2}\right) =\varphi\left(1-\frac{R_1}{R_2}\right). \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f395adb8ec1c488976b46229cde2ec7c_l3.png "Rendered by QuickLaTeX.com")
Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.
Репетитор по физике и математике
Сергей Валерьевич
© Китайская пословица
Вот такая задача: два проводящих шара радиусом R и потенциалом фи каждый находятся на расстоянии 10R друг от друга. Определить заряды шаров
Спасибо!!!
Два дня искала, почему при решении задач у заземленного тела все равно есть какой-то заряд. Спросила даже у одной учительницы физики, она сказала, что это сложно объяснить и не стала отвечать. Может и не знала.
Пожалуйста, как видите, объяснение этого факта ничуть не сложное, даже наоборот.
В третьей задаче при расчете потенциала заземленной оболочки почему оба заряда берутся при R2?
Потому что считается потенциал сферы радиуса R2.
Спасибо большое!
во второй задаче, приравнивая потенциалы шара и сферы, получим Q1/R1+Q2/R2= Q1/R2+Q2/R2. После преобразований получим R1=R2. Объясните, пожалуйста, в чем моя ошибка.
В данном случае уравнение Q1/R1+Q2/R2 = Q1/R2+Q2/R2 не является верным, так как сферы не заземлены. Это приводит к тому, что присутствует еще дополнительный индуцированный заряд, который никак не учтён в Вашем уравнении.
Вы пишете, что потенциал внешней оболочки равен k(q1+q2)/R2. здесь нет индуцированного заряда. Напишите, пожалуйста, верное уравнение.
q1 и q2 — заряды шара и внешней оболочки с учётом индуцированных. Если хотите, можно написать уравнение похожее на Ваше, только слагаемых будет больше. Слева и справа будут присутствовать члены, содержащие индуцированные и неиндуцированные заряды. Но в данном случае для решения это не нужно. Все получается из закона сохранения заряда.
Да уже даже не задача интересует, а таинственное уравнение ))
Я извиняюсь, не было времени серьезно подумать над Вашим вопросом. Действительно, Вы правы, весь заряд перетечет с шара на оболочку. Это не удивительно, потому что заряд всегда распределяется по поверхности. После того, как заряд перетечет, потенциал везде внутри оболочки станет равен потенциалу на ее поверхности kq/R2. А поскольку изначально потенциал шара был равен Phi = kq/R1, то он как раз станет равен Phi*R1/R2.
это равенство возможно, если Q1=0. Т.е. весь заряд перейдет с шара на сферу? независимо от размера шара?
Вызывает много сомнений решение задачи:В центре толстостенной металлической оболочки радиусами R1 и R2 , несущей заряд Q, находится точечный заряд q. Определить потенциал внутри и снаружи оболочки.
Каких именно сомнений?
Здравствуйте.
А у меня вызывает сомнение решение следующей задачи:
«Дана система, состоящая из двух тонких концентрических проводящих оболочек радиусами a (внутренняя) и b (внешняя). Внешняя оболочка заряжена зарядом Q, а внутренняя не заряжена. Заземляем внутреннюю оболочку. Чему равен потенциал внешней оболочки и заряд на внутренней оболочке после того, как система уравновесится?»
По логике вещей для того, чтобы после заземления потенциал внутренней оболочки стал 0, она должна получить заряд: q=-Qa/b. Но тогда потенциал внешней оболочки уменьшится: φ1 = kQ/b — kQа/(b*b)=kQ(1/b-a/(b*b)) , значит и заряд на внутренней оболочке должен соответственно измениться, чтобы сохранить ее нулевой потенциал: q=-Q(1/b-a/(b*b))*a/b и т.д.
Не подскажите, что у меня не правильно?
Спасибо, Сергей
Здравствуйте. Пусть, без нарушения общности, Q>0. В тот момент, когда внутренняя сфера не заземлена, на ней уже есть заряд, возникающий из-за индукции. Она не может быть бесконечно тонкой (хотя это не является существенным ограничением), поэтому отрицательный заряд скопится на внешней поверхности сферы (будет притягиваться с положительному Q большой сферы), а положительный — на внутренней поверхности. После заземления положительный заряд утечёт в землю, а отрицательный останется на сфере. Потенциал сферы станет равен нулю. Но этот потенциал складывается из потенциала малой и большой сферы и поэтому равен kQ/b — kq/а = 0 (где q — модуль отрицательного заряда на малой сфере). Отсюда ищем q = Qa/b (тут у Вас правильный ответ). Но этот заряд не вызывает изменения заряда на внешней сфере. Да, этот отрицательный заряд индуцирует заряд на внешней оболочке. Но и положительный и отрицательный. Закон сохранения заряда никто не отменял. А поскольку внешняя сфера не заземлена, и положительный, и отрицательный заряды остаются на сфере, а в результате друг друга компенсируют. Потенциал внешней оболочки уменьшается из-за того, что появляется отрицательный потенциал внутренней оболочки, но это никак не может сказываться на суммарном заряде внешней оболочки.
Большое спасибо за подробный ответ!
Всегда рад помочь:)
Просто и понятно, спасибо!)
Здравствуйте. Вопрос , если можно. Случай шара окруженного оболочкой которая соединена с шаром — после соединения весь заряд перетечет на внешнюю оболочку в стремлении занять наибольшие расстояния между элементарными зарядами формирующими общий заряд. А в случае двух сфер ( шаров ) не концентрических , одна из которых заряжена а другая нет что будет ? Там ведь не все заряды перетекут с одной ( малого радиуса сферы ) на другую ( большую ). Почему в одном случае весь заряд перетечет а в другом не весь ?
Здравствуйте. Чтобы не путаться в этом вопросе, лучше сказать, что заряд будет перетекать до уравнивания потенциалов сфер. Это условие существования тока. Нужна разность потенциалов, если её нет, то нет и тока. Просто в случае, когда одна сфера находится внутри другой, и они соединены проводником, уравнивание потенциалов сфер произойдёт, когда весь заряд внутренней сферы перетечёт на внешнюю (так как потенциал внутри заряженной сферы везде одинаков и равен потенциалу на поверхности, а если на внутренней сфере останется какой-то заряд, то в области между сферами потенциал будет отличаться от потенциала внутри внутренней сферы). А в случае, когда одна сфера находится снаружи первой, и они соединены проводником, для уравнивания потенциалов необходимо, что перетекла только часть заряда с одной сферы на другую (как именно часть — легко посчитать, используя формулу потенциала сферы Phi=kQ/R).
Почему после заземления сфера оказывается заряженной? Вы пишите, что положительный заряд уходит, но перемещаться могут только свободные электроны, а не положительно заряженные частицы.
Перемещаются электроны, в результате в металле остаётся избыточный положительный или отрицательный заряд. Не нужно забывать, что изначально сфера электронейтральна. В случае, когда внешний заряд отрицательный, — электроны перемещаются по заземляющему проводу от сферы, в обратном случае — дополнительные электроны перемещаются через заземляющий провод к сфере и компенсируют избыточный положительный заряд.
Действительно, внешняя сфера сначала электронейтральна, то есть положительные заряды компенсируют отрицательные. Потом эту оболочку заземляют, Земля заряжена отрицательно. То есть переход электронов на землю наблюдаться не должен, правильно? Как внешняя оболочка, будучи электронейтральноц оказывается заряженной?
Земля здесь рассматривается, как источник и вместилище заряда с очень большой электроёмкостью. На неё стекает заряд со сферы. В случае отрицательного заряда — электроны перетекают со сферы в землю, в случае положительного — из земли на сферу, но это можно рассматривать, как стекание положительного заряда со сферы в землю. Если положительный заряд на сфере притягивается к отрицательно заряженному телу (или наоборот), которое находится вблизи сферы, то этот заряд в землю не утекает, поэтому сфера остаётся заряженной.
Разве сфера не останется нейтральной при заземлении?
Прочитайте комментарий выше.
Помогите решить задачу. Толстостенная сферическая оболочка из проводящего материала имеет некоторый электрический заряд q. Чему равна напряженность электрического поля в центре оболочки?
Если оболочка проводящая и толстостенная, то весь заряд будет расположен на поверхности. Внутри в любой точке напряжённость будет равна нулю.
Вопрос к задаче 2. Если я правильно понял, при соприкосновении заряженного шара и незаряженной сферы изнутри заряд делится до выравнивания их потенциалов. А не может ли быть так: заряд на поверхности внутреннего шара q. а заряд на внутренней поверхности сферы -q, и при соприкосновении шара с внутренней поверхностью сферы заряд на шаре станет 0, останется только заряд +q на внешней поверхности сферы.
Так оно и будет.
Спасибо за примеры!
Здравствуйте, Сергей! Помогите с решением этой задачи.
Проводящий металлический шар изолирован от земли. Первоначально он заряжается при контакте с небольшим металлическим диском, несущим заряд q , так что сфера приобретает заряд Q. Затем металлическому диску снова дается заряд, а затем он касается сферы во второй раз. Если процесс повторяться бесконечно, какой будет оканчательный заряд сферы?
Здравствуйте, Сергей! Помогите с решением этой задачи.
Проводящий металлический шар изолирован от земли. Первоначально он заряжается при контакте с небольшим металлическим диском, несущим заряд q , так что сфера приобретает заряд Q. Затем металлическому диску снова дается заряд, а затем он касается сферы во второй раз. Если процесс повторяться бесконечно, какой будет оканчательный заряд сферы?
Добрый вечер, Сергей Валерьевич ! Спасибо вам большое с разбором задач подобного типа. Если б нам в институте так объясняли, то и вопросов бы не возникало.Видно я не в том институте училась.