Касательная к параболе

Автор

Воскресенье, 3 ноября, 2019
Касательная к параболе

Иногда в заданиях ЕГЭ и даже ОГЭ по математике, особенно в заданиях с параметром, возникают ситуации, когда нужно установить, при каком условии некоторая прямая касается параболы. Составить уравнение касательной к функции можно с помощью производной, и старшеклассникам обычно рассказывают в школе, как это делать. Но в случае с параболой можно обойтись без этих премудростей. Достаточно уметь решать квадратные уравнения, а этому учат уже в основой школе. В данной статье профессиональный репетитор по математике рассказывает о том, как получить уравнение касательной к параболе в некоторой точке без использования производной.

Уравнение касательной к параболе

Давайте изобразим координатную плоскость и нарисуем в ней параболу, которая проходит через начало координат. Так бывает, конечно, не всегда. Но эту проблему можно легко устранить. Достаточно просто перенести начало координат в вершину параболы, и мы получим нужную нам ситуацию. Поэтому целесообразно рассматривать именно случай, когда парабола проходит через начало координат. В этом случае уравнение такой параболы имеет вид y = ax^2:

Парабола, проходящая через начало координат

Мы для определённости взяли положительный коэффициент a, поэтому ветви данной параболы направлены вверх. Но на самом деле все дальнейшие рассуждения будут справедливы и для отрицательных a.

Отметим некоторую точку A, которая принадлежит нашей параболе. Пусть она имеет координаты (x_0;y_0). Проведём касательную к параболе в этой точке. Касательная – это прямая. А в общем виде уравнение прямой записывается как y = kx+b. То есть ситуация получается следующая:

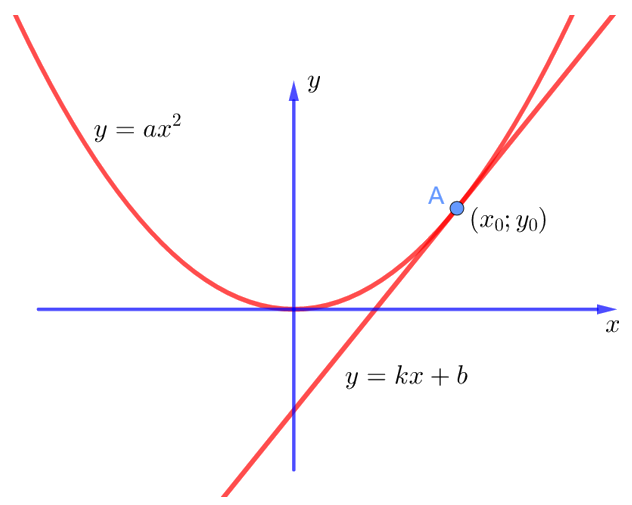
Касательная к параболе в точке

Ну и давайте зададимся целью найти неизвестные коэффициенты k и b через известные значения x_0 и a. Так у нас и получится касательная к параболе, а точнее её уравнение в точке x_0. Но давайте сразу договоримся, что делать мы это будем без помощи производной, чтобы этот материал был понятен не только старшеклассникам.

Итак, что же у нас есть? У нас есть парабола y = ax^2, причём a\ne 0. Иначе это была бы не парабола, а просто прямая линия, которая совпадает с осью OX. Также у нас есть касательная y = kx+b. Но важно то, что эта касательная и парабола имеют общую точку с координатами (x_0;y_0).

А это значит, что координаты этой точки должны удовлетворять и уравнению параболы, и уравнению касательной. Значит, если мы подставим координаты этой точки в уравнение параболы и в уравнение касательной, то мы должны при этом получить верные равенства. Итак, имеет место следующая система уравнений:

    \[ \begin{cases} y_0=ax_0^2 \\ y_0 = kx_0 + b \end{cases} \]

Именно её нам и нужно решить. Но как это сделать? Ну, во-первых, обратим сразу внимание, что у этих уравнений одинаковые левые части. А значит, равны и правые. То есть получается вот такое уравнение:

    \[ ax_0^2-kx_0-b = 0 \]

Это квадратное уравнение, которое может иметь от нуля до двух решений, в зависимости от дискриминанта. Вот здесь и возникает самая главная идея! Поскольку прямая касается параболы (ведь это касательная к параболе), то у них есть только одна общая точка. А это означает, что данное уравнение должно иметь единственное решение. Ну а единственное решение оно имеет только в том случае, если дискриминант равен нулю. Осталось его посчитать:

(1)   \begin{equation*} k^2+4ab = 0 \end{equation*}

Ну а сам корень уравнения при нулевом дискриминанте равен:

(2)   \begin{equation*} x_0 = \dfrac{k}{2a}\Rightarrow k = 2ax_0 \end{equation*}

Ну а дальше подставляем выражение (2) в уравнение (1) и получаем следующее уравнение:

    \[ 4a^2x_0^2+4ab = 0 \]

    \[ ax_0^2+b=0 \]

(3)   \begin{equation*} b = -ax_0^2 \end{equation*}

Ну и получилось, что мы смогли выразить коэффициент k и коэффициент b через a и x_0 (уравнения (2) и (3), соответственно), как и было нужно. Подставляя их в уравнение прямой, получаем искомое уравнение касательной к параболе:

y = 2ax_0x-ax_0^2

Уравнение касательной к параболе в общем виде

В общем виде парабола задаётся формулой: y = ax^2+bx+c. Как уже отмечалось выше, такую параболу можно всегда свести к параболе y = ax^2 путём простого переноса начала системы координат в вершину исходной параболы. Но зададимся вопросом, как будет выглядеть уравнение касательной к такой параболе, если мы не будем осуществлять такой перенос.

Касательная к параболе — это прямая, поэтому в общем виде уравнение этой прямой записывается по аналогии с предыдущим пунктом: y = kx+d. Только здесь мы используем букву d, поскольку буква b уже занята:

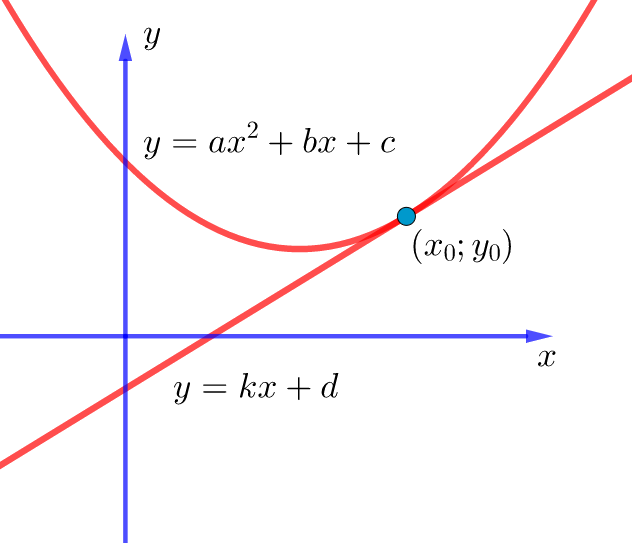
Касательная к параболе общего вида, которая не проходит через начало координат

И вновь мы ссылаемся на тот факт, что данная касательная и парабола будут иметь общую точку (x_0;y_0). Значит, координаты этой точки должны удовлетворять следующей системе уравнений:

    \[ \begin{cases} y_0 = ax_0^2+bx_0+c \\ y_0 = kx_0+d \end{cases} \]

У записанных уравнений равны левые части, значит, равны и правые. То есть имеет место следующее квадратное уравнение:

    \[ ax_0^2+bx_0+c = kx_0+d \]

    \[ ax_0^2+(b-k)x_0+c-d = 0 \]

Ну и поскольку у касательной с параболой есть только одна общая точка, то последнее уравнение должно иметь единственное решение. Такое возможно только в том случае, если его дискриминант равен нулю. То есть имеет место равенство:

(4)   \begin{equation*} D = (b-k)^2-4a(c-d) = 0 \end{equation*}

При этом сам корень уравнения должен быть равен:

(5)   \begin{equation*} x_0 = \dfrac{k-b}{2a} \Rightarrow k = 2ax_0+b \end{equation*}

Подставляем выражение (5) в выражение (4) и получаем:

    \[ (b- 2ax_0-b)^2-4a(c-d) = 0 \]

    \[ 4a^2x_0^2 - 4a(c-d) = 0 \]

    \[ ax_0^2 - c + d = 0 \]

(6)   \begin{equation*} d = c-ax_0^2 \end{equation*}

Итак, мы получили искомые коэффициенты. Значит, уравнение касательной к параболе в общем виде будет выглядеть так:

y = (2ax_0+b)x+c-ax_0^2

При этом легко убедиться, что в частном случае при b=c=0 (то есть когда парабола проходит через начало координат) мы получаем то же самое уравнение, которое уже было нами получено в предыдущем пункте.

Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич

Метки: , , ,
Опубликовано в категории Методическая копилка | 1 комментарий »

Один комментарий

  1. Адам:
    12.08.2021 в 03:25

    Спасибо!

    Ответить

Добавить комментарий