При решении многих задач, связанных с множествами, незаменимым оказывается приём, основанный на использовании так называемых «кругов Эйлера». Эти диаграммы впервые появились в работах одного из величайших математиков в истории Леонарда Эйлера, который в течение продолжительного времени жил и работал в России и был членом Петербургской академии наук. Использование кругов Эйлера добавляет наглядности при решении сложных задач, делая многие вещи буквально очевидными. Предлагаю вам в этом убедиться самостоятельно на примере решения следующей задачи.
Пример решения задачи с помощью кругов Эйлера
| 58 человек ежедневно добираются на работу общественным транспортом: на автобусе, на трамвае или на метро. Каждый пользуется хотя бы одним из видов транспорта. 42 человека из них используют метро, 32 – трамвай, 44 – автобус. 21 человек из них используют метро и трамвай, 31 – метро и автобус, 22 – трамвай и автобус. Сколько среди них человек, которые используют все три вида транспорта, чтобы добраться на работу? |
Тут нужно понимать, что если сказано, что «42 человека используют метро», то это вовсе не означает, что кроме метро они не используют никаких других видов транспорта. Кто-нибудь из них может быть и использует. Может быть ещё какой-то один вид транспорта, трамвай или автобус. А может и сразу оба! Вопрос задачи как раз и состоит в том, чтобы посчитать людей, которые используют все три вида транспорта.
С первого взгляда даже непонятно, с чего начинать решение. Но если немного поразмыслить, становится ясно, что действовать нужно по следующему алгоритму. Будем стараться расписать всех людей (58 человек) через известные из условия данные. Нам известно, что автобус используют 44 человека. Прибавим к этому количество людей, которые используют метро. Их всего 42 человек. С помощью кругов Эйлера эту операцию можно изобразить наглядно в следующем виде:
То есть пока что мы имеем дело с выражением 58 = 44 + 42… Знак «…» означает, что выражение ещё не закончено. Проблема в том, что мы посчитали людей на пересечении этих кругов дважды. Соответствующая область на диаграмме выделена тёмно-зелёным цветом. Поэтому один раз их нужно вычесть. Это люди, которые пользуются автобусом и метро. Их, как известно, 31. То есть наше «неоконченное» выражение принимает вид: 58 = 44 + 42 — 31… И на диаграмме при этом пропадает тёмно-зелёный цвет:
Пока всё хорошо. Прибавляем теперь людей, которые ездят на трамвае. Таких людей 32. Выражение принимает вид: 58 = 44 + 42 — 31 + 32… Диаграмма с кругами Эйлера, в свою очередь, становится следующей:
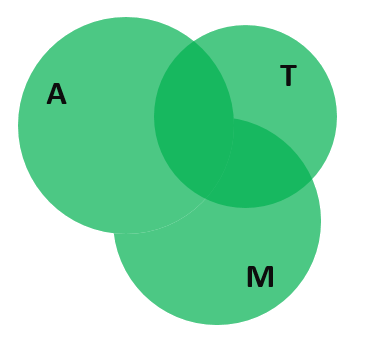
Проблема в том, что опять мы хватанули лишку. Люди, которых мы вновь посчитали дважды, отмечены на диаграмме тёмно-зелёным цветом. Эта область находится на пересечении множества, которое мы получили на предыдущем этапе, и множества людей, пользующихся трамваем.
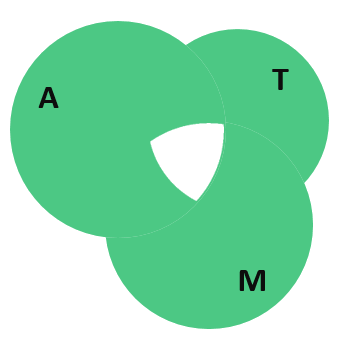
Нужно вычесть людей, которых мы посчитали дважды. Но как это сделать? Единственное, что мы можем сделать, — это разом вычесть людей, которые передвигаются на трамвае и автобусе (их 22 человека), а также на трамвае и метро (таких людей 21). После этого наше неоконченное выражение для общего количества людей примет вид: 58 = 44 + 42 — 31 + 32 — 22 — 21…, а диаграмма с кругами Эйлера окажется с дыркой в центре, потому что центральную часть мы вычли дважды:
К счастью в незакрашенной области как раз и находятся те люди, число которых нам нужно посчитать. Действительно, эти бедняги используют ежедневно все три вида транспорта для того, чтобы добраться до работы, ведь они находятся на пересечении всех трёх множеств. Обозначим количество этих бедолаг за ![]() . Тогда диаграмма примет следующий вид:
. Тогда диаграмма примет следующий вид:
А уравнение станет следующим:
![]()
Расчёты дают ![]() . Это и есть ответ к задаче. Столько людей используют все три вида транспорта каждый день, чтобы добраться на работу.
. Это и есть ответ к задаче. Столько людей используют все три вида транспорта каждый день, чтобы добраться на работу.
Вот такое вот простое решение. Фактически, в одно уравнение. Просто удивительно, не правда ли?! А теперь представьте, как пришлось бы решать эту задачу без использования кругов Эйлера. Это было бы настоящее мучение. Так что в очередной раз убеждаемся, что любые методы визуализации чрезвычайно полезны при решении задач по математике. Используйте их, это поможет вам в решении сложных задач как на олимпиадах, так и на вступительных экзаменах по математике в лицеи и вузы.
Чтобы проверить, хорошо ли вы поняли решение данной задачи, ответьте на следующие вопросы:
- Сколько человек используют только один вид транспорта для того, чтобы добраться до работы?
- Сколько человек используют для этого ровно два вида транспорта?
Свои ответы и варианты решения присылайте в комментариях.
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич

а чего здесь нет ответа
«Расчёты дают x=14. Это и есть ответ к задаче.» А к вопросам в конце статьи предполагается, что ответы дадут читатели.
спасибо большое очень выручили!
Непонятно
Нужно посмотреть видео, станет понятнее: https://www.youtube.com/watch?v=h2rhsNNWyfY
12 используют только один вид транспорта7
Да, верно. Напишите для остальных своё решение.
22 человека используют ровно 2 вида транспорта?
Нужно с решением, тогда можно будет проверить.
Жуть
58-(12+14)=32 .Человека используют только два вида транспорта.)
Да, верно.
Или :17+7+8=32
У меня получилось в первом вопросе 5.
Те кто ездит только на автобусе и метро 31-14=17
Те кто ездит только на автобусе и трамвае 22-14=8
44-17-14-8=5
Здравствуйте. Я гуманитарий, в 5-м классе мы такое не проходили, сейчас разбираем похожу задачу с сыном, поэтому — дико извиняюсь, если вопрос глупый.
Мне кажется, что центральную часть при такой последовательности действий (-31,-31, -21) мы вычитаем из общей суммы три раза, а не два, потому что она принадлежит всем трем множествам: 31, 22 и 21, тогда из выражения нужно будет вычитать не x, а 2x и правильный ответ будет 7, а не 14. Или я путаю?
Здравствуйте, нет, 7 там быть не может никак. Можно проверить. Сложим всех, кто ездит на метро, на автобусе и на трамвае. Получится 42+32+44 = 118. Но каждое из пересечений мы прибавили по два раза. Значит, по разу их нужно вычесть: 118-21-31-22 = 44. Но центральная часть при этом вычиталась 3 раза, а должна была вычитаться только 2. Значит 1 раз её нужно прибавить обратно. Значит, к 44 нужно прибавить 14, чтобы получилось 58. Правильный ответ: 14.
Я в 6 классе, сколько в учебнике читал, мама объясняла, тут читал, всё равно ничего не понял)
Ужас! Кто они вообще такие- математики? Какие нужно иметь гены, чтобы понимать математику? Может, они- инопланетяне?
Обсалютно с вами согласна!!! Я тоже очень часто задаю себе этот вопрос! Это ж каким нужно быть гением чтобы понимать эту математику!
Аааааа ты тоже тут ?!
Почему маглы используют такие непонятные вещи?
Я вот тоже не пойму… Пойду лучше спишу у Гермионы:)
Здравствуйте я ученик 6 класса и мне все понятно математику не надо понимать с ней надо просто уметь работать. И математики не иноплонетяне
Попробуйте решить в условиях —- 30 человек ежедневно добираются на работу общественным транспортом: на автобусе, на трамвае или на метро. Каждый пользуется хотя бы одним из видов транспорта. 20 человека из них используют метро, 23 – трамвай, 15 – автобус. 10 человек из них используют метро и трамвай, 12 – метро и автобус, 9 – трамвай и автобус. Сколько среди них человек, которые используют все три вида транспорта, чтобы добраться на работу? ————————————————————————————————————- А сколько при этом получится человек которые добираются только автобусом? Не получится ли отрицательное?
Если получается отрицательный результат, то схема не такая. Какое-то пересечения могут отсутствовать, или какие-то круги могут находиться внутри других.
Прямое применение Вашей формулы дает результат 3. Похоже не решение. Но на самом деле — нет. Нужна проверка на совместимость с другими условиями. Математическое решение задачи нужно доработать. А как по условию задачи проверить, что решений в натуральных числах нет?
В той задаче, которая в статье, всё корректно. Для проверки нужно посчитать значения во всех областях. Там везде получаются нормальные положительные числа. Есть ещё второй вариант решения. Через систему из нескольких линейных уравнений.
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников. Сколько учеников пользуются только одним видом транспорта ПОМОГИТЕ КРУГАМИ ЭЙЛЕРА
35-15-6+13-6+5-6+6=14
Забыла скобки прописать
35-(15-6+13-6+5-6+6)
У Вас здесь описка
35-(15-6+13-6+9-6+6)=10
Почему маглы используют такие непонятные вещи?!