Данная статья посвящена решению примеров заданий 23 из ОГЭ по математике. В этих заданиях школьников обычно просят построить график той или иной функции, а затем указать, при каких значениях параметра этот график пересекается с неким другим графиком, касается его или же, к примеру, имеет с ним несколько точек пересечения. Ну и тому подобное. В данной статье вы найдёте разбор примеров решения заданий 23 из ОГЭ по математике от профессионального репетитора, на протяжении многих лет занимающегося подготовкой школьников к этому экзамену.
Примеры решения заданий 23 из ОГЭ по математике
| Пример 1. Постройте график функции
Определите, при каких значениях |
Построение графика функции всегда нужно начинать с указания области определения этой функции. В данном случае ограничения на эту область задаются тем, что в знаменателе не должно быть нуля, потому что деление на нуль не имеет математического смысла. То есть областью определения данной функции являются все числа, за исключением 1. Записать это можно следующим образом:
![]()
После того, как мы указали область определения исходной функции, можно попробовать её упростить. Для этого вынесем минус в знаменателе за скобку и сократим. В результате получим следующее выражение:
![Rendered by QuickLaTeX.com \[ y=\frac{(x^2+0,25)(x-1)}{-(x-1)}=-x^2-0,25. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4a87d4adcaeeee08e15a3619b5ad7b7f_l3.png)
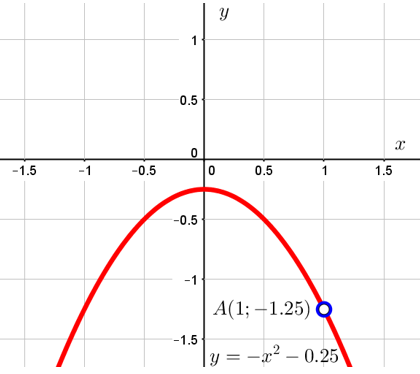
График данной функции получается из графика функции ![]() путём её отражения относительно оси OX и параллельного переноса всех точек на 0,25 единичного отрезка вниз. При этом мы должны удалить из этого графика точку
путём её отражения относительно оси OX и параллельного переноса всех точек на 0,25 единичного отрезка вниз. При этом мы должны удалить из этого графика точку ![]() , потому что она не входит в область определения исходной функции. То есть искомый график выглядит следующим образом:
, потому что она не входит в область определения исходной функции. То есть искомый график выглядит следующим образом:
Теперь отвечаем на главный вопрос задачи. Графиком функции ![]() является прямая, проходящая через начало координат. При этом в зависимости от коэффициента
является прямая, проходящая через начало координат. При этом в зависимости от коэффициента ![]() эта прямая имеет разный наклон относительно оси OX. Когда это прямая имеет ровно одну общую точку с изображённым графиком? Только в двух случаях. Рассмотрим их по отдельности.
эта прямая имеет разный наклон относительно оси OX. Когда это прямая имеет ровно одну общую точку с изображённым графиком? Только в двух случаях. Рассмотрим их по отдельности.
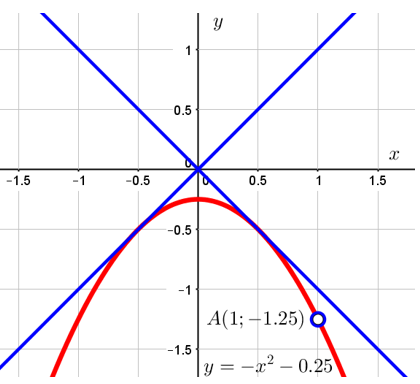
Первый случай. Когда данная прямая касается изображённого графика. Это ситуация изображена на рисунке:
Сложность состоит в том, чтобы определить значения ![]() , при которых эта ситуация реализуется. Для решения этой задачи можно использовать несколько различных подходов. Используем наиболее типичный.
, при которых эта ситуация реализуется. Для решения этой задачи можно использовать несколько различных подходов. Используем наиболее типичный.
Суть в том, что в точке касания графики проходят через одну и ту же точку на координатной плоскости. Значит, в этой точке имеет место равенство:
![]()
Дискриминант последнего квадратного уравнения равен ![]() , и в зависимости от коэффициента
, и в зависимости от коэффициента ![]() он может быть:
он может быть:
- отрицательным, тогда корней у этого уравнения не будет, как не будет и точек пересечения соответствующей прямой с изображённым графиком;
- положительным, тогда корней будет два, а значит и точек пересечения будет две (этот случай нам также не подходит);
- равен нулю, именно этот случай соответствует касанию прямой с графиком, поскольку записанное уравнение в этом случае будет иметь только одно решение.
То есть ![]() , то есть
, то есть ![]() . Соответствующие прямые как раз и изображены на рисунке выше.
. Соответствующие прямые как раз и изображены на рисунке выше.
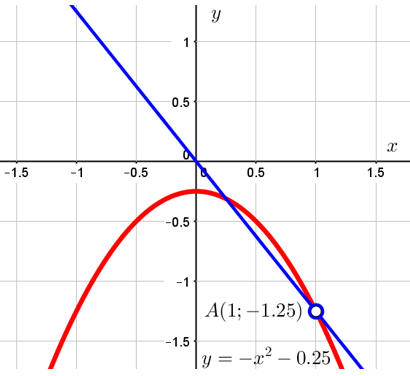
Второй случай. Не забываем, что точка с абсциссой ![]() не принадлежит нашему графику. Значит, открывается ещё одна возможность, когда прямая будет иметь с графиком ровно одну общую точку. Вот этот случай:
не принадлежит нашему графику. Значит, открывается ещё одна возможность, когда прямая будет иметь с графиком ровно одну общую точку. Вот этот случай:
Для нахождения ![]() в этом случае подставляем координаты точки
в этом случае подставляем координаты точки ![]() в уравнение прямой
в уравнение прямой ![]() . В результате получаем
. В результате получаем ![]() .
.
Ответ: ![]() .
.
| Пример 2. Постройте график функции
Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс? |
Сразу отметим, что в область определения данной функции входят все числа: ![]() . Наша задача теперь, как это часто бывает при решении заданий 23 из ОГЭ по математике, состоит в том, чтобы построить график этой функции. Для тех кто не сталкивался ранее с подобными заданиями, это может показаться странным, но график данной функции можно построить из графика функции
. Наша задача теперь, как это часто бывает при решении заданий 23 из ОГЭ по математике, состоит в том, чтобы построить график этой функции. Для тех кто не сталкивался ранее с подобными заданиями, это может показаться странным, но график данной функции можно построить из графика функции ![]() . Нужно только выделить в подмодульном выражении полный квадрат. Для этого проведём следующие преобразования:
. Нужно только выделить в подмодульном выражении полный квадрат. Для этого проведём следующие преобразования:
![Rendered by QuickLaTeX.com \[ y=\left|x^2-x-2\right| = \left|x^2-2\cdot\frac{1}{2}x+\frac{1}{4}-2\frac{1}{4}\right|. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c4b3ad13743284ea88b7e932390dedc1_l3.png)
Из последнего с помощью формулы «квадрат разности» получаем:
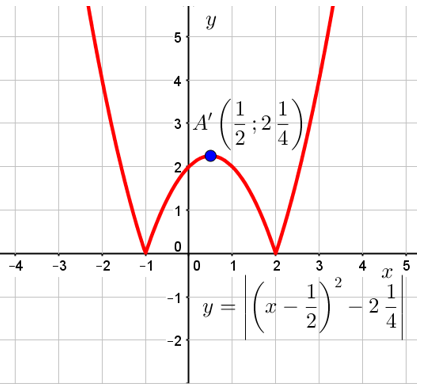
![Rendered by QuickLaTeX.com \[ y=\left|\left(x-\frac{1}{2}\right)^2-2\frac{1}{4}\right|. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-282f1f03025a8fc52244c883dad966c2_l3.png)
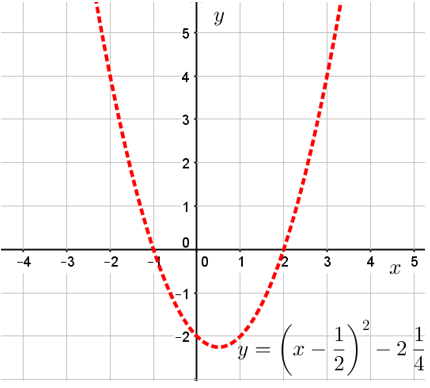
Построим сначала график функции ![]() . Этот график получается из графика функции
. Этот график получается из графика функции ![]() путём его переноса на
путём его переноса на ![]() единичного отрезка вправо и на
единичного отрезка вправо и на ![]() единичного отрезка вниз:
единичного отрезка вниз:
При этом нули функции равны 2 и -1. Что произойдёт с этой параболой, если взять модуль от всего выражения, стоящего справа? Все точки, лежащие ниже оси OX (с отрицательными ординатами), отразятся вверх относительно оси OX. В результате получится вот такой график:
Теперь, глядя на этот график, уже понятно, что максимальное число точек пересечения данного графика с линией, параллельной оси абсцисс, будет равно 4. В качестве примера можно взять прямую ![]() :
:
Ответ: 4.
Вот так решаются задания 23 из ОГЭ по математике. Как я уже говорил, это довольно интересные задания, которые к тому же можно научиться решать по ясному и запоминающемуся алгоритму. И как только вы овладеете этим мастерством, все задачи 23 из ОГЭ по математике будут казаться вам простыми и даже очевидными. Это станет для вас ещё одним заветным ключиком, который поможет получить максимальный балл на экзамене. Так что желаю вам успехов в подготовке и удаче на экзамене!
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич


Сергей Валерьевич,огромное спасибо!
Спасибо!Помогли.
Спасибо большое! Очень понятно все объяснили.
Спасибо очень доходчиво объясняете. Но вопрос, почему x=1 не водящий в область определения, берется для нахождения k? Разве не x=-1 нужно брать? Может я не поняла что-то. Заранее спасибо.
В область определения не входит x=1 (знаменатель не может быть равен нулю), поэтому на графике этой точки нет (она выколота). Поэтому нужно брать именно эту точку.
А почему бы в задании с модулем не выделять квадрат двучлена, а просто построить параболу по алгоритму отрицательную часть графика симметрично отразить относительно оси ОХ.Результат будет тот же, а построение проще. Спасибо.
Да, конечно, можно и так. Просто у меня в этой статье была цель показать, как разные операции влияют на вид графика.
Спасибо
Сергей Валерьевич! Помогите пожалуйста! Недавно моя дочка писала пробник ОГЭ по математике и вот какая разновидность 23ей задачи там попалась. Что вы про нее скажете?
https://otvet.mail.ru/question/207815034
Довольно типичное задание. График строится по стандартному алгоритму, а прямая при изменении k вращается вокруг точки (3;4). Больше одной общей точки будет при k>=1.
При всех k>=1? если посмотреть график, то можно обнаружить множество прямых с углом наклона близким к 90 градусов, которые пересекут параболу один раз «внизу», а «наверху» правую ветвь параболы уже не заденут… поэтому я решила, что у множества значений k должен быть верхний порог
Нет, квадратичная функция растёт быстрее линейной, поэтому там всегда будет вторая точка пересечения.
Спасибо большое! Вы мне очень помогли!
Всегда пожалуйста, рад был помочь.
СПАСИБО!
А нужно ли проводить все эти прямые,о которых спрашивается в задании?То есть,если просят указать значения К,но не просят строить эти прямые
Лишним это точно не будет. К тому же это займёт на экзамене 1 минуту. Так что лучше всё же построить, как мне кажется.
Мне это не нужно было, но я прочитал. Спасибо!
Спасибо!
Задание2 можно было найти ось симметрии, а затем приравнять всю функцию к нулю, после найти точки пересечения с осью х. Потом провести прямую параллельную абциссе, тем самым найти точки пересечения.
большое спасибо автору