Разбор заданий части 1 ЕГЭ по математике

Автор

Четверг, 21 июля, 2016

В данной статье представлен разбор заданий первой части профильного ЕГЭ по математике от репетитора. Доступен также видеоурок с подробным разъяснением решений всех рассмотренных заданий. Идеально для тех, кто начал готовиться к ЕГЭ по математике «с нуля».

1. Для отслеживания расхода холодной воды в квартире установлен счётчик. Его показания 1 января составляли 103 куб. м, а 1 февраля— 114 куб. м. Сколько в рублях потребуется заплатить за холодную воду за январь, если стоимость 1 куб. м составляет 19 руб. 20 коп.?

Всего за январь было израсходовано 114-103 = 11 куб. м  холодной воды. Значит заплатить потребуется 19,2×11 = 211,2 руб.

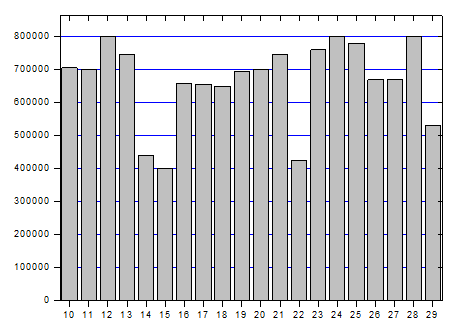
2. На графике представлены данные посещаемости (по вертикали отложено количество посетителей) новостного сайта с 10 по 29 апреля 2012 года (по горизонтали отложены числа месяца). Во сколько раз наибольшее количество посетителей в день превышает наименьшее количество посетителей в день за указанный период.

Зависимость числа посетителей от дня месяца из задания 2 первой части ЕГЭ по математике профильного уровня

Из рисунка видно, что максимальное количество посетителей, соответствующее наиболее высокому столбику на диаграмме, составляло 800000 (12, 24 и 28 апреля). А минимальное количество посетителей, соответствующее наименее высоком столбику на диаграмме, составляло 400000 (15 апреля). Значит наибольшее количество посетителей за день было в 2 раза больше наименьшего.

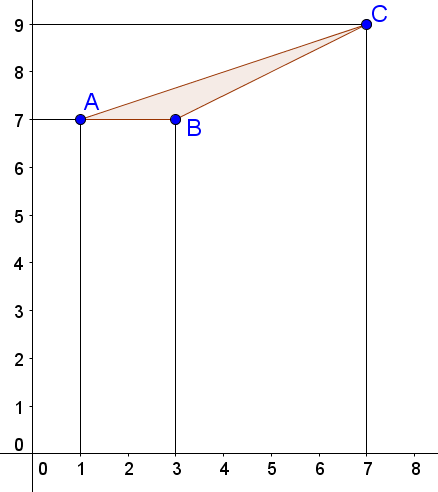
3. Найдите площадь треугольника, изображённого на рисунке.

Треугольник, площадь которого нужно найти, из задания 3 первой части ЕГЭ по математике

Площадь треугольника вычисляется по формуле: S=\frac{1}{2}ah_a, где a — сторона треугольника, ha — высота, проведенная к этой стороне. Длина стороны AB треугольника ABC, изображённого на рисунке, равна 2. Длина высоты, проведённой к этой стороне из точки C, равна 2 (подробное объяснение, почему это так, смотрите в видеоуроке). Тогда площадь треугольника равна: S = \frac{1}{2}\cdot 2\cdot 2 = 2.

4. В состязании прыгунов в длину участвуют 8 спортсменов из Нидерландов, 6 спортсменов из Франции, 5 спортсменов из Египта и 5 — из Нигерии. Порядок их выступления определяется с помощью лототрона. Найдите вероятность того, что прыгун из Франции выступит последним.

Благоприятных вариантов для такого исхода — 6 (так как 6 спортсменов из Франции), всевозможных вариантов исхода — 24 (так как всего спортсменов: 8+6+5+5 = 24). Тогда искомая вероятность равна отношению числа благоприятных исходов к числу всевозможных исходов и равна \frac{6}{24}=\frac{1}{4}.

5. Найдите корень уравнения:

    \[ 2^{4x-14}=\frac{1}{64}. \]

Заметим сразу, что \frac{1}{64} = \frac{1}{2^6} = 2^{-6}. Тогда приходим к следующему уравнению:

    \[ 2^{4x-14}=2^{-6}. \]

Две степени с одинаковым основанием равны тогда и только тогда, когда равны их показатели. То есть имеет место равенство:

    \[ 4x-14 = -6\Leftrightarrow 4x = 8\Leftrightarrow x = 2. \]

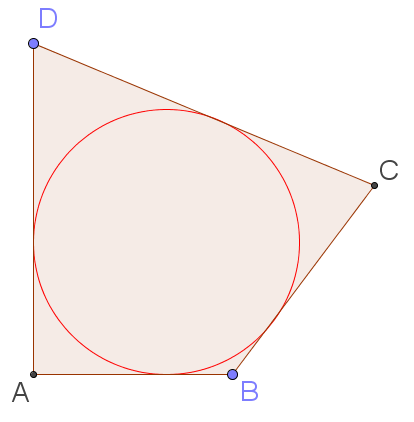
6. Периметр четырехугольника ABCD равен 48. Известно, что в этот четырёхугольник можно вписать окружность. Известно также, что АВ = 15. Найдите CD.

Окружность, вписанная в четырёхугольник, из задания 6 первой части ЕГЭ по математике

Поскольку в данный четырёхугольник вписана окружность, то суммы его противоположных сторон равны. Следовательно, AB + CD = AD + BC = 48/2 = 24. Тогда CD = 24 — AB = 24 — 15 = 9.

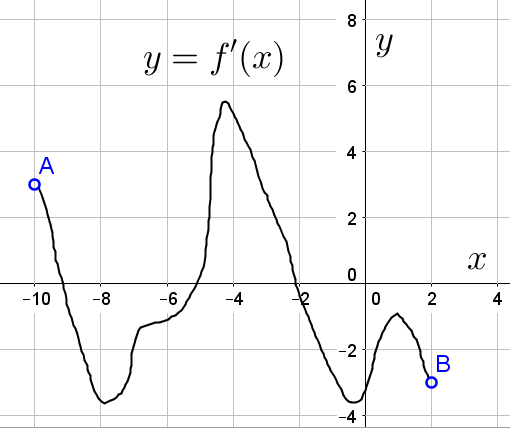
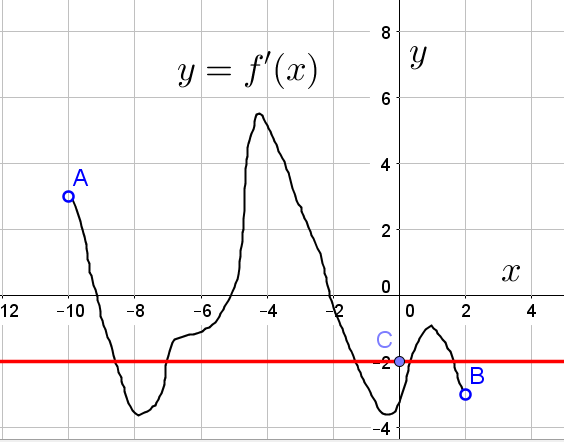
7. На рисунке изображён график y=f'(x) производной функции f(x), которая определена на промежутке (-10;2). Найдите число точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x-11 или совпадает с ней.

График производной функции из задания 7 первой части профильного варианта ЕГЭ по математике

Чтобы касательные графику функции y=f(x) были параллельны прямой y=-2x-11 или совпадали с ней, их коэффициенты при переменной x (так называемые коэффициенты наклона) должны быть равны -2. Значение данных коэффициентов в соответствии с геометрическим смыслом производной равно значению производной функции в точке касания. То есть требуется найти количество точек, в которых производная функции равна -2.

Для этого изображаем на графике прямую, параллельную оси Ox и проходящую через точку (0;-2):

График производной функции с вспомогательной линией из задания 7 профильного ЕГЭ по математике

Считаем количество точек пересечения данной прямой с графиком производной функции. Таких точек 5. Это и есть ответ к заданию.

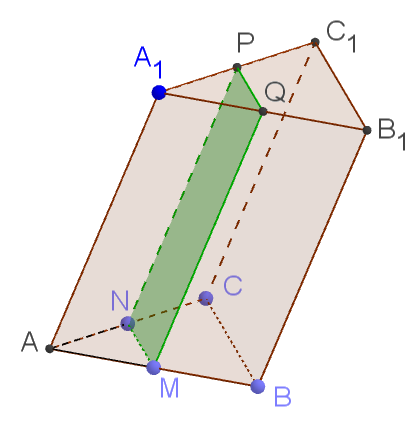
8. Площадь боковой поверхности треугольной призмы ABCA1B1C1 равна 24. Через эту призму проведено сечение MNPQ, параллельное ребру BB1, причём MN — средняя линия треугольника ABC. Найдите площадь боковой поверхности треугольной призмы AMNA1QP.

Наклонная треугольная призма из задания 8 ЕГЭ по математике

Стороны оснований треугольной призмы AMNA1QP будут в два раза меньше сторон оснований треугольной призмы ABCA1B1C1.  Боковые стороны стороны треугольной призмы AMNA1QP будут равны боковым сторонам треугольной призмы ABCA1B1C1. То есть площадь каждой боковой грани треугольной призмы AMNA1QP в два раза меньше площади соответствующей грани треугольной призмы ABCA1B1C1. То есть площадь боковой поверхности отсечённой призмы в 2 раза площади боковой поверхности исходной призмы: \frac{24}{2} = 12.

Разбор заданий первой части профильного ЕГЭ по математике представлен репетитором по математике в Москве, Сергеем Валерьевичем

Смотрите также разборы задач 13, 14, 18 из профильного ЕГЭ по математике

Метки: , , ,
Опубликовано в категории Методическая копилка | Нет комментариев »

Добавить комментарий