Разбор заданий вступительного экзамена по математике в МГУ 2013 года

Автор

Среда, 31 июля, 2013

Разбор заданий вступительного экзамена по математике в МГУ 2013

Московский Государственный Университет (МГУ) по праву считается лучшим вузом страны. Поступление в МГУ – это возможность получить по-настоящему современное и качественное образование, которое ценится не только в нашей стране, но и за рубежом. В 2013 году счастливыми обладателями студенческого билета МГУ имени Ломоносова стали 7,5 тысяч вчерашних абитуриентов, а конкурс при поступлении в среднем по университету превысил семь человек на место.

Традиционно МГУ принимал абитуриентов, оценивая три основных параметра: результаты ЕГЭ, победы в олимпиадах, а также дополнительные вступительные экзамены по математике и другим профильным направлениям. Из этих трех составляющих складывались баллы, и по конкурсу проводилось зачисление в университет. По словам ректора старейшего российского вуза традиционно профильный экзамен помогает преподавателям «увидеть в поступающем склонности и отметить его талантливость».

Надо сказать, в этом году возможностей для раскрытия своих талантов у сдающих экзамен по математике действительно было достаточно. Экзамен оказался не из простых. В данной статье представлен разбор одного варианта вступительного экзамена по математике в МГУ, проходившего 17 июля 2013 года.

Задача 1. Старший коэффициент квадратного трехчлена f(x) равен 2. Один из его корней равен \frac{5}{2}. Найдите второй корень, если известно, что f(0)=3.

Решение. В общем виде квадратный трехчлен записывается следующим образом: ax^2+bx+c. Поскольку старший коэффициент равен 2, то наш квадратный трехчлен принимает вид: 2x^2+bx+c.

Известно также, что при x=0, значение квадратного трехчлена равно 3. То есть имеет место равенство: 2\cdot 0^2 + b\cdot 0 + c = 3, из которого находим, что c=3.

Поскольку одним из корней квадратного трехчлена является число \frac{5}{2}, то при подстановке этого значения вместо x,  значение квадратного трехчлена становится равным 0. Таким образом имеет место равенство: 2\cdot\frac{25}{4}+b\cdot\frac{5}{2}+3=0. Откуда находим, что b = -\frac{31}{5}.

Итак, квадратный трехчлен имеет вид: 2x^2-\frac{31}{5}x+3. Приравниваем его к нулю: 2x^2-\frac{31}{5}x+3 = 0. Делим обе части уравнения на 2: x^2-3.1x+1.5=0. По теореме Виета сумма корней этого уравнения равна 3.1. Поскольку первый корень равен 2.5, второй корень равен 0.6=\frac{3}{5}.

Ответ: \frac{3}{5}

Задача 2. Вычислите \log_{12}3\cdot\log_9 12.

Решение. Для решения этого задания потребуются следующие формулы преобразования логарифмических выражений:

    \[ \log_a b = \frac{1}{\log_b a},\, a,b>0,\, a,b\ne 1, \]

    \[ \log_a b^n = n\log_a b,\, a,b>0,\, a\ne 1. \]

Используя приведенные выше формулы, преобразуем исходное выражением к вид:

    \[ \log_{12}3\cdot\log_9 12 = \frac{\log_{12} 3}{\log_{12} 3^2}=\frac{\log_{12} 3}{2\log_{12} 3} = \frac{1}{2}. \]

Ответ: \frac{1}{2}.

Задача 3. Решите неравенство

    \[9\left(1+5^{1-2x}\right)^{-\frac{1}{2}}-\frac{1}{2}\left(5^{2x}+5\right)^{\frac{1}{2}}\geqslant 6^{\frac{1}{2}}\cdot 5^{\frac{x}{2}}.\]

Решение. Представим неравенство в виде:

    \[ 9\left(\frac{5^{2x}}{5^{2x}+5}\right)^{\frac{1}{2}}-\frac{1}{2}\left(5^{2x}+5\right)^{\frac{1}{2}}\geqslant 6^{\frac{1}{2}}\cdot 5^{\frac{x}{2}}. \]

Разделим обе части неравенства на 5^{\frac{x}{2}}>0, в результате чего получим неравенство:

    \[ 9\left(\frac{5^x}{5^{2x}+5}\right)^{\frac{1}{2}}-\frac{1}{2}\left(\frac{5^{2x}+5}{5^x}\right)^{\frac{1}{2}}\geqslant 6^{\frac{1}{2}}. \]

Введем новую переменную: t = \left(\frac{5^x}{5^{2x}+5}\right)^{\frac{1}{2}}.  Легко видеть, что t>0. Тогда исходное неравенство принимает вид: 9t-\frac{1}{2t}\geqslant \sqrt{6} или \frac{18t^2-2\sqrt{6}t-1}{2t}\geqslant 0.

Последнее неравенство решается методом интервалов. Решением является следующая совокупность:

    \[ \left[\begin{array}{l} t\geqslant \frac{1}{\sqrt{6}}, \\ -\frac{1}{3\sqrt{6}}\leqslant t<0.\end{array} \]

Двойное неравенство игнорируем, поскольку t>0. Решаем только первое неравенство. Возвращаясь к исходной переменной, получаем неравенство:

    \[ \frac{5^x}{5^{2x}+5}\geqslant \frac{1}{6}. \]

После упрощений получаем:

    \[ 5^{2x}-6\cdot 5^x+5\leqslant 0. \]

Это стандартное показательное неравенство, его решением является промежуток: x\in[0;1].

Ответ: x\in[0;1].

Задача 4. Решите уравнение

    \[\frac{\sin 5x}{\sin x}-\frac{\cos 5x}{\cos x}=\frac{\sin x}{\sin 5x}-\frac{\cos x}{\cos 5x}.\]

Решение. Перепишем уравнение в виде:

    \[ \frac{\sin 5x}{\sin x} + \frac{\cos x}{\cos 5x} = \frac{\sin x}{\sin 5x} + \frac{\cos 5x}{\cos x}. \]

Приведем выражения к общему знаменателю:

    \[ \frac{\sin 5x\cos 5x + \sin x\cos x}{\sin x\cos 5x}=\frac{\sin x\cos x+\sin 5x\cos 5x}{\sin 5x\cos x}. \]

Числители обеих дробей одинаковы. Преобразуем их отдельно к виду:

    \[ \sin 5x\cos5x + \sin x\cos x = \frac{1}{2}\left(\sin 10x+\sin 2x\right) = \]

    \[ =\frac{1}{2}\cdot 2\sin 6x\cos 4x = \sin 6x\cos 4x. \]

Тогда после переноса всего в одну сторону и приведения к общему знаменателю получаем:

    \[ \frac{\sin 6x\cos 4x\left(\sin5x\cos x-\cos 5x\sin x\right)}{\sin x\cos x\sin 5x\cos 5x} = 0. \]

После использования формулы «синус разности» получаем:

    \[ \frac{\sin 6x\cos 4x\sin 4x}{\sin x\cos x\sin 5x\cos 5x} = 0. \]

Дробь равна нулю, когда ее числитель равен нулю, а знаменатель не равен нулю. Таким образом имеет место следующая смешанная система:

    \[ \begin{cases} \left[\begin{array}{l} \sin 6x = 0, \\ \cos 4x = 0, \\ \sin 4x = 0, \end{array} \\ \sin x \ne 0, \\ \cos x \ne 0, \\ \sin 5x \ne 0, \\ \cos 5x \ne 0. \end{cases} \Leftrightarrow \begin{cases} \left[\begin{array}{l} x = \frac{\pi n}{6},\, n\in Z, \\ x = \frac{\pi}{8}+\frac{\pi k}{4},\, k\in Z, \\ x = \frac{\pi m}{4},\, m\in Z, \\ \end{array} \\ x \ne \pi b,\, b\in Z, \\ x \ne \frac{\pi}{2}+\pi c,\, c\in Z, \\ x \ne \frac{\pi d}{5},\, d\in Z, \\ x \ne \frac{\pi}{10}+\frac{\pi l}{5},\, l\in Z, \\ \end{cases} \]

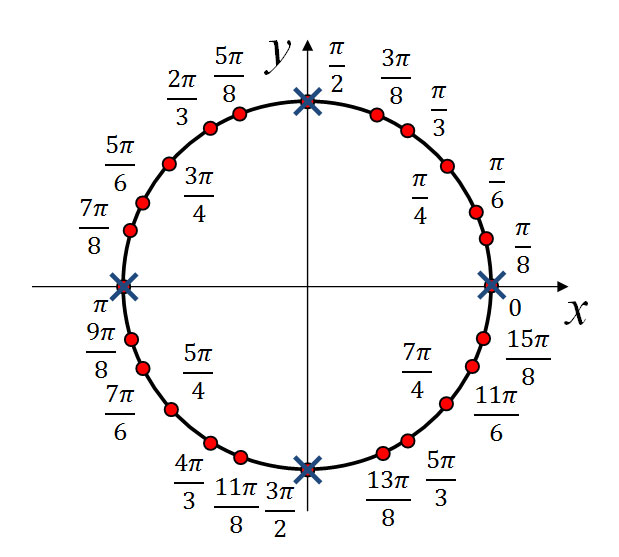
На единичной окружности значения x, определяемые равенствами, отметим точками. Исключим из них крестиками значения x, определяемые неравенствами.

Рисунок к задаче 4 из вступительного экзамена в МГУ от 17 июля 2013 года. Единичная окружность

Единичная окружность с изображенными решениями полученных равенств и неравенств

Разобравшись в рисунке, получаем отчетливое представление, что в качестве решений уравнения можно взять серии: x=\frac{\pi k}{8},\, k\in Z при этом k\ne 4n,\, n\in Z и x=\frac{\pi m}{6},\, m\in Z при этом m\ne 3q,\, q\in Z.

Ответ:

x = \frac{\pi k}{8},\, k\in Z,\, k\ne 4n,\, n\in Z,

x=\frac{\pi m}{6},\, m\in Z,\, m\ne 3q,\, q \in Z.

Задача 5. В 14:00 из села Верхнее вниз по течению реки в сторону села Нижнее отправился катер «Быстрый». Когда до Нижнего оставалось плыть 500 метров, ему навстречу из Нижнего вышел катер «Смелый». В этот же самый момент «Быстрый», не желая встречи со «Смелым», развернулся и пошел обратно к Верхнему. В 14:14, когда расстояние по реке от «Быстрого» до Верхнего сравнялось с расстоянием по реке от «Смелого» до «Быстрого», на «Смелом» осознали, что они идут с «Быстрым» на одинаковой скорости, развернулись и направились обратно к Нижнему. В исходные пункты катера вернулись одновременно в 14:18. Найдите расстояние по реке между Верхним и Нижним, если известно, что оба катера движутся равномерно и с одинаковой скоростью.

Решение. Введем следующие обозначения. Пусть x — искомое расстояние по реке между Верхним и Нижним, y — собственная скорость катеров, v — скорость течения реки. Время будем считать в часах, расстояние в километрах, скорость, соответственно, в километрах в час. Из условия ясно, что на дорогу «туда и обратно» катеру «Быстрому» потребовалось 18 минут. На языке введенных обозначений это условие можно записать в виде уравнения:

    \[ \frac{18}{60}=\frac{x-0.5}{y+v}+\frac{x-0.5}{y-v}. \]

После разворота катера «Быстрого» оба катера стали двигаться с одинаковой скоростью, то есть расстояние между ними оставалось равным 500 метров. В 14:14 оно стало равно расстоянию от «Быстрого» до «Верхнего». Следовательно, оставшееся время, а именно 4 минуты, «Быстрый» преодолевал эти 500 метров. На языке введенных обозначений это условие записывается в виде:

    \[ \frac{0.5}{y-v}=\frac{4}{60}. \]

Раз так, то расстояние от «Смелого» до Нижнего в момент времени 14:14 стало равным x-1, а все оставшееся время, а именно 4 минуты, он преодолевал как раз это расстояние:

    \[ \frac{x-1}{y+v}=\frac{4}{60}. \]

Из второго уравнения получаем: y-v = 7.5, из третьего: y+v=15(x-1). После подстановки в первое уравнение получаем:

    \[ 0.3=\frac{x-0.5}{15(x-1)}+\frac{x-0.5}{7.5}. \]

Решениями последнего уравнения являются значения: x=2 и x=1.25. Последнее не подходит, поскольку в этом случае получается отрицательное значение скорости v.

Ответ: 2 км.

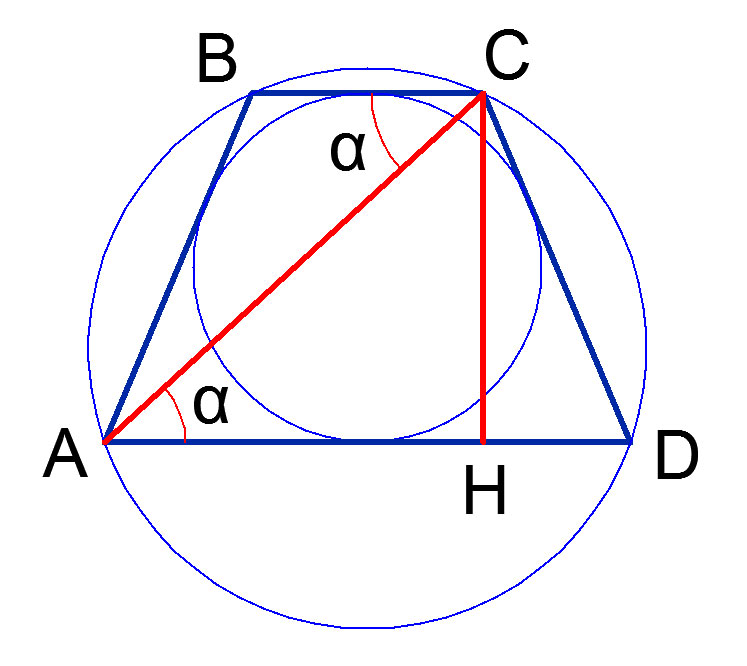
Задача 6. Трапеция ABCD вписана в окружность радиуса R и описана около окружности радиуса r. Найдите r, если R=12, а косинус угла между диагональю AC и основанием AD равен \frac{3}{4}.
Трапеция, вписанная в окружность и описанная около окружности

Чертеж к задаче 6 вступительного экзамена по математике 2013 в МГУ

Решение. Находим сразу, что \sin\angle CAD = \sin\alpha = \frac{\sqrt{7}}{4}. В трапеции ABCD проведем высоту из точки C, основание этой высоты назовем H. Окружность, описанная около трапеции, описана также и вокруг треугольника ACD. Используя теорему синусов для этого треугольника, получаем, что CD = 2R\sin\alpha = \ 6\sqrt{7}. Окружность может быть описана только вокруг равнобедренной трапеции, поэтому AB = 6\sqrt{7}.

Пусть BC = a, AD = b. Поскольку в трапецию вписана окружность, то суммы противолежащих сторон трапеции равны. То есть a+b=12\sqrt{7}. Кроме этого \angle CAD = \angle ACB = \alpha, поскольку являются накрест лежащие при параллельных прямых BC, AD и секущей AC.

Записываем теоремы косинусов для треугольников ABC и ACD:

    \[ \begin{cases} (6\sqrt{7})^2=a^2+AC^2-2aAC\cos\alpha, \\ (6\sqrt{7})^2=b^2+AC^2-2bAC\cos\alpha. \end{cases} \]

Вычитанием из первого уравнения второго получаем после преобразований: 2AC\cos\alpha=a+b=12\sqrt{7}. Откуда с учетом \cos\alpha = \frac{3}{4} получаем, что AC = 8\sqrt{7}. Далее из треугольника ACH находим высоту трапеции: CH = AC\sin\alpha = 14. Радиус окружности, вписанной в трапецию, равен половине этой высоты, то есть 7.

Ответ: 7.

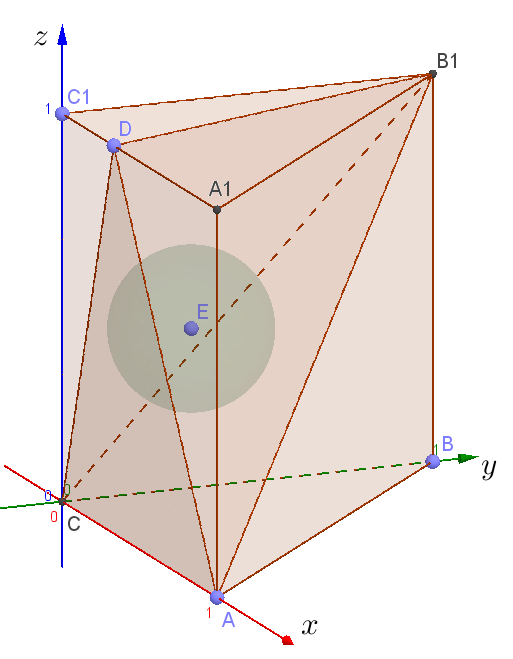
Задача 7. В основании прямой призмы ABCA_1B_1C_1 лежит прямоугольный треугольник ABC, такой что AC = BC = 1. На ребре A_1C_1 верхнего основания (параллельном AC) отмечена точка D, так что A_1D : DC_1 = 2 : 1. Найдите радиус сферы, вписанной в тетраэдр AB_1CD, если высота призмы равна 1.

Решение. Введем прямоугольную декартову систему координат следующим образом. Ось OZ направим в направлении ребра CC_1, ось OX — в направлении ребра CA, ось OY — в направлении ребра CB.

Картинка с вписанной в тетраэдр сферой из задания по стереометрии из вступительного экзамена по математике в МГУ

В качестве единичного отрезка возьмем длину высоты призмы. Ищем координаты точек A, B_1, C, и D в этой системе координат: C(0;0;0), A(1;0;0), B_1(0;1;1) и D\left(\frac{1}{3},0,1\right). Тогда имеем четыре уравнения плоскостей:

    \[ \begin{array}{l} AB_1C: \, y-z=0 \\ ADC: \, y=0 \\ AB_1D: \, 3x+y+2z-3=0 \\ CDB_1: \, 3x+y-z=0 \end{array} \]

Пусть центр сферы имеет в этой системе координаты (x_0, y_0, z_0), а ее радиус равен \rho. Поскольку сфера вписана в тетраэдр, то расстояния от ее центра до каждой из указанных выше плоскостей одинаковы. То есть имеет место система уравнений:

    \[ \begin{cases} \frac{|y_0-z_0|}{\sqrt{2}}=\rho, \\ y_0=\rho, \\ \frac{|3x_0+y_0+2z_0-3|}{\sqrt{14}}=\rho, \\ \frac{|3x_0+y_0-z_0|}{\sqrt{11}}=\rho. \end{cases} \]

Решая полученную систему относительно искомого радиуса \rho, и с учётом условия, что каждое из чисел x_0, y_0, z_0 и \rho положительно и не превосходят 1, получаем: \rho = \left(1+\sqrt{2}+\frac{\sqrt{11}}{3}+\frac{\sqrt{14}}{3}\right)^{-1}.

Ответ: \left(1+\sqrt{2}+\frac{\sqrt{11}}{3}+\frac{\sqrt{14}}{3}\right)^{-1}.

Задача 8. Найдите все значения параметра a, при которых уравнение \sin\left(x+\frac{a}{x}\right)=x+1 имеет бесконечно много решений.

Решение. Отметим сразу, что уравнение может иметь решения только при x\in[-2;0). При a=0 уравнение принимает вид: \sin x = x+1. Последнее уравнение на промежутке [-2;0) не имеет бесконечного количества решений, поскольку графики функций f(x) =\sin x и f(x) = x+1 пересекаются на этом промежутке в одной точке.

Рассмотрим теперь случай, когда a\ne 0. Пусть t=\operatorname{arcsin} (x+1). Тогда x — корень уравнения, если x+\frac{a}{x}=t+2\pi k,\, k\in Z. Иначе x+\frac{a}{x}-\operatorname{arcsin}(x+1)=2\pi k. Поскольку функции f(x) = x, f(x) = \operatorname{arcsin(x+1)} непрерывны и ограничены при x\in[-2;0), а функция f(x) = \frac{a}{x} непрерывна и не ограничена при x\in[-2;0), то функция F(x) = x+\frac{a}{x}-\operatorname{arcsin}(x+1) также непрерывна и не ограничена при x\in [-2;0). Следовательно, при a\ne 0 функция F(x) принимает значения, кратные 2\pi, бесконечное число раз, и исходное уравнение имеет в этом случае бесконечно много решений.

Ответ: a\ne 0.

Материал подготовлен репетитором по математике для подготовки к вступительному экзамену в МГУ, Сергеем Валерьевичем

Метки: , ,
Опубликовано в категории Методическая копилка | 28 комментариев »

Комментарии

  1. Р:
    15.08.2013 в 22:57

    Вариант-то простенький выдался, первые 6 задач вообще проходные. Эх, мельчает МГУ, то-то варианты 2000-2006 годов мехмат и вмк

    Ответить
    1. Sergey Seliverstov:
      16.08.2013 в 08:24

      Сейчас для всех факультетов один вариант, может из-за этого. Да и абитуриентов сейчас мало по сравнению с нулевыми, кризис рождаемости 90-х. А дальше еще меньше будет, вплоть до 2015-2016. Хотя на МГУ это, конечно, в меньшей степени сказывается. Плюс еще ЕГЭ же остается. Так что по совокупности факторов, как говорится.

      Ответить
  2. Людмила:
    06.07.2014 в 18:42

    у меня возник вопрос при просмотре решения задачи №5.я не совсем поняла,почему расстояние от «Смелого» до Нижнего в момент времени 14:14 стало равным x-1 .Я была бы очень благодарна,если бы мне смогли здесь разъяснить это.

    Ответить
    1. Sergey Seliverstov:
      07.07.2014 в 08:56

      Дело в том, что после разворота «Быстрого» оба катера стали двигаться с одинаковой скоростью, а значит расстояние между ними всегда оставалось равным 500 м. По условию в 14:14 расстояние по реке от «Быстрого» до Верхнего сравнялось с расстоянием по реке от «Смелого» до «Быстрого», то есть также стало равным 500 м. Итак, расстояние от «Смелого» до Верхнего стало равным 500 м + 500 м = 1 км. Так как за x (в км) мы обозначили расстояние от Верхнего до Нижнего, то расстояние от «Смелого» до Нижнего в момент времени 14:14 стало равным именно x-1.

      Ответить
  3. Людмила:
    07.07.2014 в 11:30

    Спасибо

    Ответить
  4. Андрей:
    08.07.2014 в 23:10

    Здравствуйте! Может я не по теме, но как вы думаете какие примерно задачи будут в 2014 году? К каким типам задач нужно готовиться больше? Спасибо! С уважением Андрей!

    Ответить
    1. Sergey Seliverstov:
      09.07.2014 в 16:17

      Здравствуйте! Может быть что угодно, никогда не угадаешь:). Как в своё время говорил мой школьный учитель: «Учить всё!»
      Вот Вам для разминки задание:
      http://yourtutor.info/wp-content/uploads/2014/07/MSP214241gaha7f2ia855g92000017d0cif4gfgh7998-1.gif
      Ответ хороший, без иррациональностей, при правильном подходе задание не требует громоздких вычислений.

      Ответить
  5. Марина:
    09.07.2014 в 09:12

    У меня с математикой всегда проблемы: (

    Ответить
  6. Влад:
    10.07.2014 в 16:38

    Подскажите, пожалуйста. Не очень понял третий номер, а точнее, как из 18t^2-2… получили ответ (разложили).

    Ответить
    1. Влад:
      10.07.2014 в 16:54

      Вся, понял!

      Ответить
  7. Радиф Галиевич:
    14.08.2014 в 13:42

    1.При решении первого задания нахождение второго коэффициента квадратного трехчлена — избыточно. Чтобы найти второй корень квадратного трехчлена достаточно свободный член (а он уже найден и равен 3) разделить на старший коэффициент , затем результат разделить на известный корень (первая часть теоремы Виета).
    2. Задача 7 очень легко решается элементарно-геометрическим способом (без применения метода координат и прочих заморочек аналитической геометрии). При этом поможет известная формула, связывающая объем описанного многогранника (в т.ч. пирамиды) с радиусом вписанного шара (сферы) и площадью полной поверхности многогранника: V=1/3*R*S (И.Ф.Шарыгин / Геометрия 10-11). Здесь легко получить: V=1/6, несложно вычислить площадь всех 4 граней тетраэдра.

    Ответить
    1. Sergey Seliverstov:
      24.01.2015 в 10:38

      Как говорил мой преподаватель по математике, хорошая задача всегда имеет множество решений.

      Ответить
  8. Камолов Умед:
    24.08.2014 в 10:28

    ого

    Ответить
  9. Камолов Умед:
    24.08.2014 в 10:33

    Я то думал сложный будет а тут простые задачи

    Ответить
  10. Мария:
    10.03.2015 в 14:43

    Задания с параметрами вызывают больше всего затруднений, так как в школе не рассматриваются.

    Ответить
    1. Sergey Seliverstov:
      15.03.2015 в 21:37

      Поэтому и из ЕГЭ их убрали…

      Ответить
  11. фаршед:
    18.07.2015 в 13:39

    сколько время выдается для решение всех этих задач

    Ответить
    1. Sergey Seliverstov:
      21.07.2015 в 19:28

      4 астрономических часа

      Ответить
      1. 28/06/2016:
        28.06.2016 в 13:13

        Сергей, а можете помочь с задачей того же года, но про катера «Первый» и «Второй», отправляющиеся из пунктов «А» и «Б».
        Там не сказано, что они шли с одинаковой скоростью.

        Ответить
        1. Сергей:
          29.06.2016 в 08:42

          Да, но при этом есть дополнительное условие. Сказано, что второй катер одновременно с первым стартовал из исходного пункта.

          Ответить
  12. Александр:
    13.07.2016 в 21:04

    В 6 опечатка в конце, CH = AC sina = 14, не тангенс

    Ответить
    1. Сергей:
      13.07.2016 в 22:07

      Спасибо. Опечатку исправил.

      Ответить
  13. Вячеслав:
    14.07.2016 в 12:38

    Добрый день !
    Не могу понять, как решить систему уравнений в 7-ой задаче. Решая, оперирую тем, что х0, у0 ,z0 > 0, исходя из введённой системы координат. Неясно как в финальной стадии однозначно раскрыть модуль
    | sqrt(11)*p+3sqrt(2)*p+3p — 3 | .
    Также пытался получить радиус исходя из формулы
    p=sqrt(x0^2 + y0^2 +z0^2). Получается отрицательная ерунда.
    Помогите, пожалуйста !

    Ответить
    1. Сергей:
      15.07.2016 в 00:04

      Добрый день. Там проблемы, кажется, нет никакой. Подставляем в первое уравнение r(ро) вместо y0. Пусть r>z0, раскрываем модуль с плюсом, тогда получаем r-z0=корень(2)r, откуда z0=(1-корень(2))r. Но это невозможно, т.к. z0>0. Следовательно, раскрыть можно только со знаком минус. Получаем -r+z0=корень(2)r, откуда получаем z0=(1+корень(2))r. Далее подставляем это в последнее уравнение, выражаем аналогично x0 через r. Подставляем всё в третье уравнение, и там получается ответ.

      Ответить
  14. Никита:
    12.01.2017 в 10:26

    Здравствуйте, а не можете, пожалуйста, подсказать, почему в 8 здании x∈[-2;0)? И по каким сборникам можно подготовиться к задачам с параметром?

    Ответить
    1. Сергей:
      12.01.2017 в 11:26

      Здравствуйте, потому что область значений синуса от -1 до 1, но 0 икс равен быть не может, поскольку он стоит в знаменателе. К вступительному экзамену в МГУ можно готовиться по пособию Ткачука «Математика абитуриенту».

      Ответить
  15. Никита:
    12.01.2017 в 15:55

    Сергей, огромное спасибо за ответ!

    Ответить
  16. Сергей:
    30.04.2018 в 21:54

    Почему в 4 задании 2 и 3 серии корней не входят в ответ?

    Ответить

Добавить комментарий