
Часто при решении задач, связанных с множествами, возникают ситуации, когда для наглядности гораздо удобнее изобразить эти множества графически. Для этого используют так называемые круги Эйлера. В этой статье речь пойдёт о решении задачи с помощью сразу трёх кругов Эйлера.
Задача с тремя кругами Эйлера
|
В классе 35 человек. Известно, что музыкой занимается 13 человек, танцами – 15 человек, плаванием – 20 человек, музыкой и танцами – 4 человека, музыкой и плаванием – 6 человек, плаванием и танцами – 7 человек, музыкой, плаванием и танцами – 1 человек. Есть ли в классе ученики, которые не увлекаются никакими из перечисленных занятий? Если да, то сколько их? |
Итак, как же нам решить такую задачу? Те, кто с такими задачами сталкивался, знают, что их очень удобно решать с помощью так называемых кругов Эйлера.
Нам известно, что музыкой занимается 13 человек. Давайте изобразим этих людей с помощью круга, имея в виду, что все эти люди как бы находятся внутри этого круга. Чтобы это подчеркнуть, иногда даже ставят точки внутри этих кругов. Каждая точка символизирует человека. Но мы этого делать не будем. Лучше потом подпишем числами. Итак получаем вот такой круг:
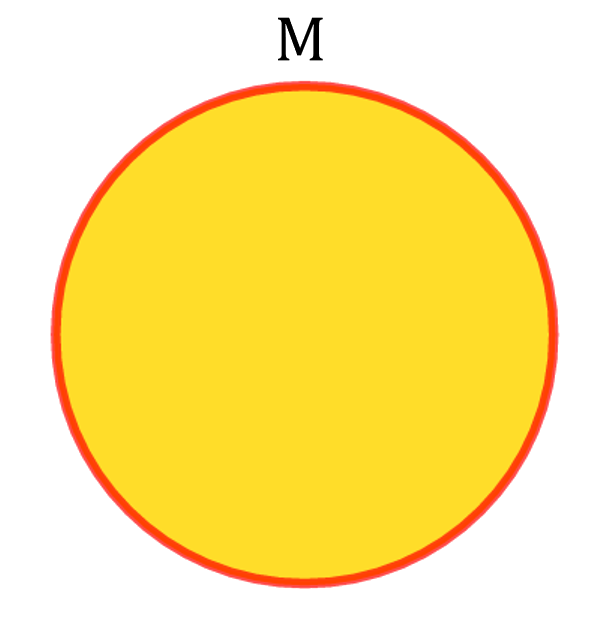
Танцами занимается 15 человек. Это ещё один круг Эйлера. Причём! Он находится не где-то совершенно отдельно от первого, а в обязательном порядке пересекается с первым! Почему? Потому что мы знаем, что есть люди, которые занимаются и музыкой, и танцами. И на нашей диаграмме они должны быть расположены на пересечении этих кругов. Вот так:

Отлично! Теперь переходим к тем, кто занимается плаванием. Их ровно 20. То есть это ещё один «круг людей», который пересекается одновременно с первым кругом, потому что есть люди, занимающиеся музыкой и плаванием, и со вторым, так как есть люди, которые и плавают, и танцуют. То есть получается вот такая комбинация, содержащая 3 круга Эйлера:
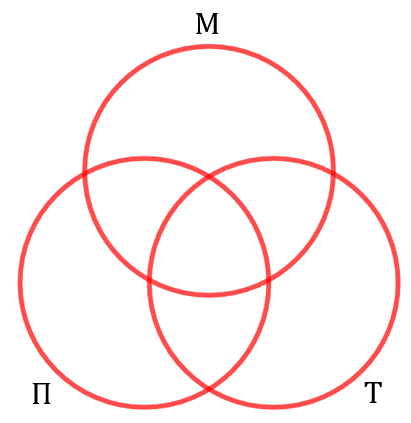
Но как же решать задачу? Мы с вами ещё не использовали последнее условие. У нас есть такой уникально одарённый человек, который занимается одновременно и музыкой, и плаванием, и танцами. На нашей диаграмме он находится в том месте, где пересекаются все три круга. То есть в центре. И теперь давайте числами отмечать, сколько людей у нас находится в каждой из получившихся областей. Итак, в центральной части диаграммы у нас находится один человек:

Но тогда! Поскольку мы знаем, что музыкой и танцами занимается 4 человека, а в центральной области находится 1 человек, то в соседней правой области, как легко сообразить, находится ![]() человека:
человека:
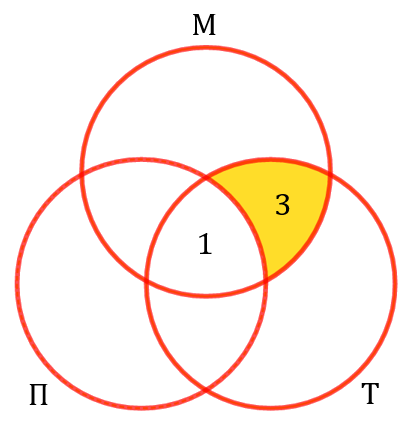
Вычисляем теперь аналогично, сколько человек находится во всех областях на диаграмме, которые соседствуют с центральной. Поскольку музыкой и плаванием занимается 6 человек, то в области левее центральной находится ровно ![]() человек. Кроме того, если плаванием и танцами занимается 7 человек, то в области ниже центральной находится
человек. Кроме того, если плаванием и танцами занимается 7 человек, то в области ниже центральной находится ![]() человек:
человек:
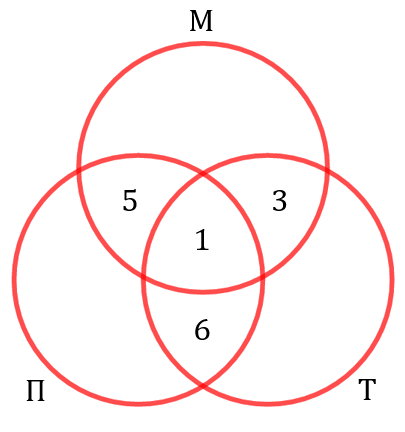
Очень хорошо! Но это ещё не всё. У нас остались белые пятна на диаграмме. Давайте их устраним. Как это сделать? Теперь вспоминаем, что музыкой увлекается 13 человек. Значит, в самой верхней части верхнего круга находится ![]() человека:
человека:
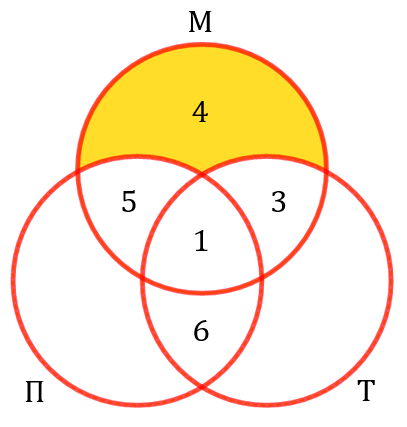
Аналогично, поскольку танцуют у нас 15 человек, то в самой правой части правого круга находится ровно ![]() человек. Ну и поскольку пловцов у нас 20, то в самой левой части левого круга находится ровно
человек. Ну и поскольку пловцов у нас 20, то в самой левой части левого круга находится ровно ![]() ребят. Итак, мы узнали, сколько и где у нас находится людей:
ребят. Итак, мы узнали, сколько и где у нас находится людей:
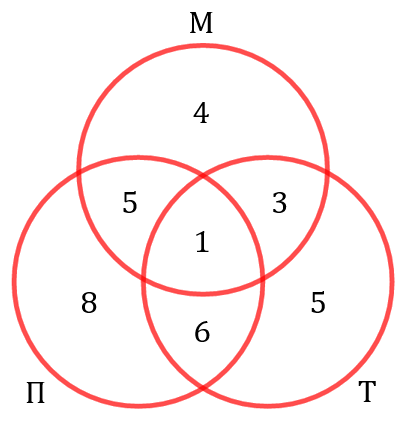
Ну а теперь… Чтобы узнать, сколько человек занимается хотя бы одном каким-то видом увлечений из перечисленных (музыкой, плаванием или танцами), нужно просто сложить все эти числа. Их сумма равна ![]() . Но всего в классе 35 человек. Это означает, что есть ровно
. Но всего в классе 35 человек. Это означает, что есть ровно ![]() человека, которые не увлекаются ни одним из перечисленных занятий. И это наш ответ.
человека, которые не увлекаются ни одним из перечисленных занятий. И это наш ответ.
Вот такая задача. Эта задача, кстати, была на вступительном экзамене в лицей №1580 в 2018 году. Её решали шестиклассники, которые поступали, соответственно, в 7 класс этого лицея. Я являюсь репетитором по математике и физике и готовлю школьников к вступительным экзаменам в различные школы Москвы, в том числе в лицей 1580. Если вам требуется такая подготовка, обращайтесь ко мне. Мой контакты вы найдёте на этой странице.
Материал подготовил репетитор по математике и физике в Москве Сергей Валерьевич
