Решение задач из контрольной работы по общей физике

Четверг, 15 марта, 2012

Многие ученики задаются вопросом, насколько то, что они изучают по физике в школе проще, чем то, что изучается по физике в вузе. Является ли школьный курс «детским лепетом» по сравнению с настоящей физикой как наукой. Многим школьникам, в том числе отличникам, физика дается не просто. Оно и понятно, ведь это объективно наиболее трудный для понимания предмет из изучаемых в школе.

Мне посчастливилось преподавать физику и в школе, и в вузе, а потому об отличиях одного от другого я знаю не понаслышке. Та физика, которую ученики постигают в школе, называется «элементарной», но это вовсе не делает ее простой! Без преувеличения будет сказано, что основной целью изучения физики в школе является подготовка учащихся к жизни в современном мире, формирование их общего мировоззрения, а также своеобразного базиса, без которого невозможно изучение физики в вузе. Вспомните свои школьные годы, и вам станет ясно, насколько это сложная задача для учителя, решить ее может далеко не каждый. Всякий педагог должен с пониманием относиться к тем трудностям, с которыми сталкиваются школьники при изучении физики в их возрасте.

Для того, чтобы наглядно продемонстрировать разницу в образовательных программах и уровне преподавания физики в школе и вузе, предлагаю вашему вниманию разбор контрольной работы по общей физике для первого курса университета МИИТ. Ознакомьтесь, возможно, это окажется для вас полезным.

Задача 1. Фотон с длинной волны $\lambda_1 = 15$ пм рассеялся на свободном электроне. Длина волны рассеянного фотона $\lambda_2 = 16$ нм. Определить угол $\theta$ рассеяния.

Решение.

Иллюстрация к эффекту Комптона

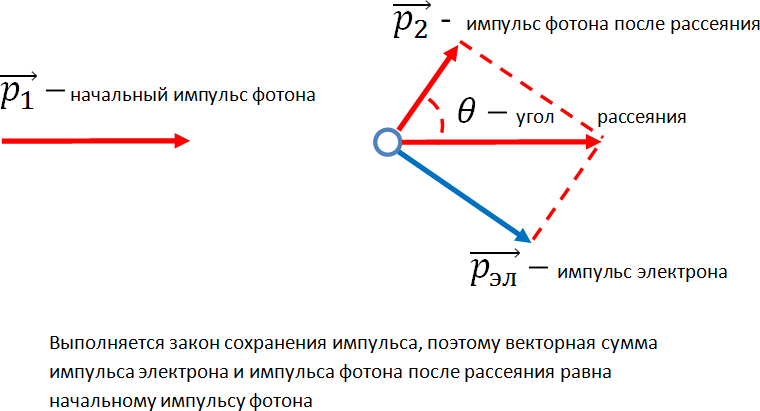
Изменение длины волны фотона происходит вследствие эффекта Комптона: $\lambda_2-\lambda_1 = \lambda_K (1-\cos\theta),$ где $\lambda_2$ — длина волны излучения после рассеяния, $\lambda_1$ — длина волны излучения до рассеяния, $\theta$ — угол рассеяния, $\lambda_K = \frac{h}{m_e c} = 2,4\cdot 10^{-12}$ м — комптоновская длина волны электрона.

Выражая угол рассеяния $\teta,$ получаем:

$\theta = \operatorname{arccos}\left(1-\frac{\lambda_2-\lambda_1}{\lambda_K}\right) =$

$=\operatorname{arccos}\left(1-\frac{16\cdot 10^{-12}-15\cdot 10^{-12}}{2,4\cdot 10^{-12}}\right) = 54^0.$

Задача 2. Вычислить длину волны де Бройля в пучке протонов, имеющих скорость $10^3$ м/с. Надо ли учитывать волновые свойства, если диаметр пучка 1 мм?

Решение.

Длина волны де Бройля вычисляется по формуле: $\lambda = \frac{h}{p}$ , где $h=6,63\cdot 10^{-34}$ Дж·с — постоянная Планка, $p$ — импульс протона. Импульс при движении частицы со скоростью, много меньшей скорости света, определяется по формуле: $p = m\upsilon$ , где $m=1,67\cdot 10^{-27}$ кг — масса протона, $\upsilon$ — скорость движения протона.

Подставляя все в исходную формулу, получаем:

$\lambda = \frac{h}{m\upsilon} = \frac{6,63\cdot 10^{-34}}{1,67\cdot 10^{-27}\cdot 10^3} = 4\cdot 10^{-10} \operatorname{M}.$

По сравнению с диаметром пучка в 1 мм, данным в условии в качестве характерного размера, эта величина чрезвычайно мала. Волновые свойства в данном случае учитывать не нужно.

Задача 3. В сосуде находится $m_1=14$ г азота и $m_2=9$ г водорода при температуре $t^0=10^0C$ и давлении $P = 1$ МПа. Найдите молярную массу $\mu$ смеси и объем $V$ сосуда.

Решение.

Считаем газы идеальными, то есть каждый из них занимает весь объем сосуда $V$ , и общее давление смеси равно сумме парциальных давлений каждого из газов (закон Дальтона): $p = p_1+p_2$ . Запишем уравнение Менделеева-Клапейрона для каждого из газов и для всей смеси в целом:

$\begin{cases}p_1V = \frac{m_1}{\mu_1}RT, \\ p_2V = \frac{m_2}{\mu_2}RT, \\ pV = \frac{m_1+m_2}{\mu}RT\end{cases}\Leftrightarrow \begin{cases} p_1 = \frac{m_1}{\mu_1V}RT, \\ p_2 = \frac{m_2}{\mu_2V}RT, \\ p = \frac{m_1+m_2}{\muV}RT \end{cases}\Leftrightarrow$

$p = p_1+p_2 = \frac{m_1+m_2}{\mu V}RT = \frac{m_1}{\mu_1V}RT + \frac{m_2}{\mu_2V}RT\Leftrightarrow$

$\frac{m_1+m_2}{\mu} = \frac{m_1\mu_2+m_2\mu_1}{\mu_1\mu_2}\Leftrightarrow \mu = \frac{\mu_1\mu_2(m_1+m_2)}{m_1\mu_2+m_2\mu_1}.$

Здесь $\mu_1 = 28\cdot 10^{-3}$ кг/моль — молярная масса азота, $\mu_2 = 2\cdot 10^{-3}$ кг/моль — молярная масса водорода. Считаем, по структуре формулы видно, что вычисления можно проводить в граммах и граммах на моль:

$\mu = \frac{28\cdot 2\cdot(14+9)}{14\cdot 2+9\cdot 28} = 4,6 \operatorname{g/mol}.$

Из третьего уравнения исходной системы выражаем объем, получаем:

$V = \frac{m_1+m_2}{\mu}\frac{RT}{p} = \frac{14\cdot 10^{-3}+9\cdot 10^{-3}}{4,6\cdot 10^{-3}}\cdot\frac{8,31\cdot 283}{10^6} =$

$=12\cdot 10^{-3} \operatorname{M}^3.$

Задача 4. При нормальных условиях динамическая вязкость азота $\eta = 17$ мкПа·с. Найдите среднюю длину $\bar{l}$ свободного пробега молекул газа. Молярная масса азота $\mu = 28\cdot 10^{-3}$ кг/моль.

Решение.

Коэффициент динамической вязкости в кинетической теории газов определяется соотношением: $\eta = \frac{1}{3}\bar{u}\bar{l}\rho$ , где $\bar{u}$ — средняя скорость теплового движения молекул, $\bar{l}$ — средняя длина свободного пробега молекул газа, $\rho$ — плотность газа.

Плотность азота при нормальных условиях можно определить из уравнения Менделеева-Клапейрона:

$p = \frac{\rho}{\mu}RT\Leftrightarrow \rho = \frac{p\mu}{RT}.$

Среднюю тепловую скорость движения молекул азота при нормальных условиях определяется по формуле:

$\bar{u}=\sqrt{\frac{8RT}{\pi\mu}}.$

Подставляя все в исходную формулу, получаем:

$\eta = \frac{1}{3}\frac{p\mu}{RT}\sqrt{\frac{8RT}{\pi\mu}}\cdot\bar{l}\Leftrightarrow\bar{l} = \frac{3\eta}{p}\sqrt{\frac{\pi RT}{8\mu}},$

здесь $T=273$ К — температура газа при нормальных условиях, $p=10^5$ Па — давление газа при нормальных условиях. Вычисляем:

$\bar{l} = \frac{3\cdot 17\cdot 10^{-6}}{10^5}\sqrt{\frac{3,14\cdot 8,3\cdot 273}{8\cdot 28\cdot 10^{-3}}} = 9\cdot 10^{-8}\operatorname{M}.$

Задача 5. 1 кмоль азота, находящегося при нормальных условиях, расширяется адиабатически от объема $V_1$ до объема $V_2 = 5V_1$ . Найдите изменение внутренней энергии газа и работу, совершенную при расширении.

Решение.

Поскольку процесс адиабатический, для начального и конечно состояния газа верно равенство: $\frac{T_2}{T_1} = \left(\frac{V_1}{V_2}\right)^{\gamma-1}$ , здесь $\gamma$ — показатель адиабаты. Азот — двуатомный газ, поэтому для него $\gamma = 1.4$ . Тогда получаем, что $\frac{T_2}{T_1} = 5^{1-1.4} = 0,53$ , то есть $T_2 = 0,53 T_1$ .

Изменение внутренней энергии вычисляется по формуле: $\Delta U = \frac{i}{2}\nu R \Delta T$ , где $i$ — число степеней свободы молекулы газа, для двуатомного газа $i=5$ , $R = 8,31$ Дж / (моль·К) — универсальная газовая постоянная.

Получаем: $\Delta U = \frac{5}{2}\nu R (0,53T_1 - T_1) = -1,18\nu R T_1.$ Газ находится при нормальных условиях, поэтому $T_1= 273$ К. Вычисляя, получаем: $\Delta U = - 2,7$ МДж (знак минус говорит о том, что внутренняя энергия уменьшилась).

Адиабатический процесс идет без теплообмена, поэтому Первый закон термодинамики для него записывается в виде: $A = -\Delta U$ , где $A$ — работа, совершаемая газом в процессе. Значит искомая работа равна $A = 2,7$ МДж.

Задача 6. Количество вещества кислорода равно $\nu = 0,5$ моль. Определите внутреннюю энергию кислорода, а также среднюю кинетическую энергию молекулы этого газа при температуре $T = 300$ К.

Решение.

Внутренняя энергия газа определяется по формуле: $U = \frac{i}{2}\nu R T$ , где $i$ — число степеней свободы молекулы газа, кислород — двуатомный газ, для него $i=5$ , $R = 8,31$ Дж / (моль·К) — универсальная газовая постоянная. Считаем: $U = \frac{5}{2}\cdot 0,5\cdot 8,31\cdot 300 = 3,1$ кДж.

Средняя кинетическая энергия молекулы газа по Больцману определяется следующим образом: $\overline{E_K} = \frac{i}{2}kT,$ где $k=1,38\cdot 10^{-23}$ Дж/К — постоянная Больцмана.

Считаем: $\overline{E_K} = \frac{5}{2}\cdot 1,38\cdot 10^{-23}\cdot 300 = 10^{-20}$ Дж.

Задача 7. Какого цвета будет звезда, если температура ее поверхности $T = 4000$ К? Какую энергию излучает звезда за 1 секунду с единицы поверхности?

Решение.

Для ответа на первый вопрос, используя закон смещения Вина. Определим какой длине волны соответствует максимум излучения нагретого тела при температуре 4000 К: $\lambda_m = \frac{b}{T}$ , здесь $b = 2,9\cdot 10^{-3}$ м·К — постоянная Вина. Считаем: $\lambda_m = \frac{2,9\cdot 10^{-3}}{4000} = 725$ нм. Это длина волны красного цвета.

Энергия, излучаемая с единицы поверхности за одну секунду, есть энергетическая светимость. Для того, чтобы ее найти, воспользуемся законом Стефана-Больцмана: $R=\sigma T^4$ , где $\sigma = 5,67\cdot 10^{-8}$ Вт/(м²·К⁴) — постоянная Стефана-Больцмана. Считаем: $R = 5,67\cdot 10^{-8}\cdot 4000^4 = 1,45\cdot 10^7$ Вт/м².

Задача 8. Ядро урана $_{92}^{238}U$ испуская α-частицу с энергией 4,2 МэВ, превращается в ядро тория $_{90}^{234}Th.$ Определите массу атома $_{90}^{234}Th$ , если масса атома $_{92}^{238}U$ равна 238,1251 а.е.м.

Решение.

Уравнение данной реакции имеет вид: $_{92}^{238}U \rightarrow _{90}^{234}Th + _2^4He$ . Масса протона равна $m_p = 1,007276$ а.е.м., масса нейтрона $m_n = 1,008665$ а.е.м.

Ищем дефект масс для ядра урана:

$92m_p+(238-92)m_n - 238,1251 =$

$=92\cdot 1,007276 + 146\cdot 1,008665 - 238,1251 =$

$=1,809382\operatorname{a.e.m.} = \frac{1,809382}{931,5} = 1685,4\operatorname{MeB}.$

Здесь мы использовали, что $c^2 = 931,5$ МэВ/а.е.м. Непосредственно α-частице из этого достанется 4,2 МэВ энергии, остальные $1685,4-4,2=1681,2$ МэВ или $\Delta m = \frac{1681,2}{931,5}=1,804873$ а.е.м. придутся на дефект масс ядра тория. Зная это, вычисляем массу атома тория:

$90m_p + (234-90)m_n-\Delta m =$

$90\cdot 1,007276 + (234-90)\cdot 1,008665 - 1,804873 =$

$= 234,097727\operatorname{a.e.m.}$

Задача 9. Два параллельных световых пучка, отстоящих друг от друга на расстоянии $d=5$ см, падают на кварцевую призму $(n=1,49)$ с преломляющим угол $\alpha = 25^0.$ Определите оптическую разность хода $\Delta$ этих пучков на выходе их из призмы.

Два параллельных луча преломляются в призме

Геометрический ход лучей в задаче

Решение.

Из геометрии рисунка определяем, что $l_1=d_1\operatorname{tg}\alpha,$ а $l_2 = d_2\operatorname{tg}\alpha.$ Вычитанием первого уравнения из второго получаем, что $l_2-l_1 = (d_2-d_1)\operatorname{tg}\alpha=d\operatorname{tg}\alpha.$

$l_2-l_1$ — геометрическая разность хода лучей, она связана с искомой оптической разностью хода $\Delta$ соотношением $\Delta = n(l_2-l_1),$ где $n$ — показатель преломления среды, в которой распространяется свет (в данном случае кварца). После подстановок и вычислений получаем: $\Delta = nd\operatorname{tg}\alpha = 1,46\cdot 2\cdot\operatorname{tg}25^0 = 1,36$ см.

Задача 10. Угол падения $i_1$ луча на поверхность стекла равен $60^0.$ При этом отраженный луч оказался максимально поляризованным. Определите угол $r$ преломления луча.

Иллюстрация к задаче

Решение.

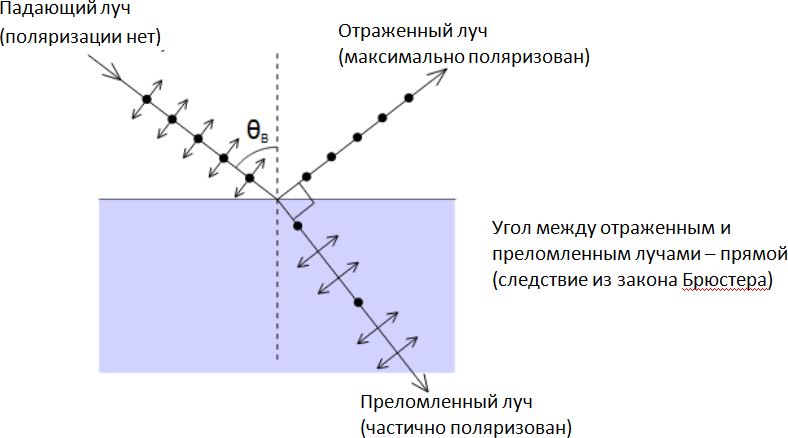
Поскольку отраженный от стекла (диэлектрика) луч максимально поляризован, то луч падает на поверхность стекла под углом Брюстера. В такой ситуации в соответствии со следствием из закона Брюстера угол между отраженным и преломленным лучами равен $90^0.$ Известно также, что угол падения равен углу отражения. Тогда из геометрии рисунка искомый угол равен: