Поступление в школу 1329 с репетитором

Как репетитор по математике я готовлю школьников к поступлению в школу 1329 в районе Тропарёво-Никулино г. Москвы. Эта как раз мой район, поэтому из года в год ко мне обращаются родители с просьбой помочь с поступлением в это учебное заведение. В данной статье я решил разобрать типовой вариант вступительного экзамена по математике в 5 класс школы №1329 за 2018 год. Думаю, что этот материал будет полезен для тех, кто готовится к поступлению в школу 1329 с репетитором или самостоятельно.

Представленные формулировки не являются копией тех заданий, что были на самом вступительном экзамене. Но задания составлены таким образом, что они полностью соответствуют вступительному экзамену в 5 класс школы 1329. Так что, попробовав решить их самостоятельно, вы как бы окажитесь на самом экзамене. Ну а проверить свои решения вы можете самостоятельно, сравнив их с моими подробными авторскими решениями, которые я публикую здесь в открытом доступе.

Разбор вступительного экзамена по математике в 5 класс школы 1329

Задание 1. Найдите значение выражения:

Основным требованием при выполнении этого задания является то, чтобы все вычисления должны быть представлены в чистовике. Вот образец верного оформления решения:

Ответ: 137066.

Задание 2. Решите уравнение:

Поступление в школу 1329 с репетитором предполагает, конечно, обучение мастерству решения уравнений. Здесь мы имеем дело с самым простым типом уравнений, которые изучаются ещё в младшей школе. На самом деле такие задания решаются по одному простому алгоритму. Необходимо определить порядок действий и двигаться от последнего действия к первому, заменяя каждое действие обратным. Вот образец верного оформления решения:

   

Ответ: 2639.

Задание 3. У Алёши был кусок картона прямоугольной формы и ножницы. Алёша начал резать этот картон, причём делил его следующим образом: каждый раз одним разрезом ножницами отрезал от прямоугольника квадрат. В результате получил 2 больших квадрата, 1 средний и 4 маленьких. Сторона каждого маленького квадрата оказалась равна 3 см. Найдите площадь исходного картонного прямоугольника.

Решаем задачу «с конца»:

• Последние 4 маленьких квадратика со сторонами по 3 см можно было получить только по очереди, разрезая полоску шириной 3 см и длиной 4 × 3 = 12 см.
• Тогда сторона среднего квадрата равна 12 см, поэтому его можно было получить только из прямоугольника шириной 12 см и длиной 12 + 3 = 15 см.
• Тогда сторона каждого большого квадрата равна 15 см, поэтому каждый из них можно было получить только из прямоугольника шириной 15 см и длиной 12 + 2 × 15 = 42 см.
• Площадь такого прямоугольника равна 42 × 15 = 630 кв. см.

Для наглядности изобразим этот прямоугольник на рисунке:

Ответ: 630 кв. см.

Задание 4. В банке налито молоко. Маша выпила 189 г молока из этой банки, а затем ещё 213 г. В результате в банке стало в 3 раза меньше молока, чем было первоначально. Сколько грамм молока было в банке первоначально?

Всего Маша выпила 189 + 213 = 402 г молока. Поскольку в банке молока стало в 3 раза меньше, чем было, то осталось 1/3 часть молока. Значит, Маша выпила 2/3 от всего молока. Теперь, чтобы найти сколько молока было в банке первоначально, нужно 402 поделить на 2 и умножить на 3. В итоге получаем 402 : 2 × 3 = 603 г.

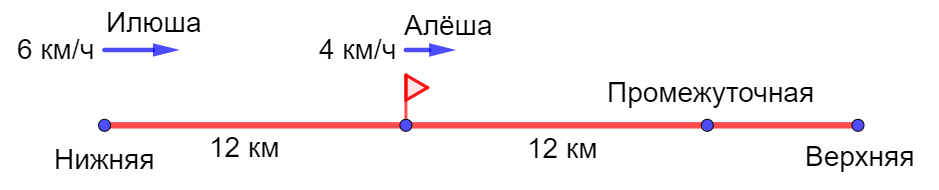
Задание 5. По дороге от деревни Нижняя до деревни Верхняя есть деревня Промежуточная. Алёша вышел из Нижней в направлении Верхней со скоростью 4 км/ч. Через 3 часа, когда Алёша оказался на полпути между Нижней и Промежуточной, ему вслед из Нижней отправился Илюша со скоростью на 2 км/ч большей, чем у Алёши. Когда Алёша дошёл до Промежуточной, он присел отдохнуть на полчаса, а затем отправился дальше. В результате оказалось, что Алёша и Илюша пришли в Верхнюю в одно и то же время. Чему равно расстояние между деревнями Нижняя и Верхняя?

Поскольку Алёша прошёл полпути от Нижней до Промежуточной за 3 часа, двигаясь со скоростью 4 км/ч, то расстояние от Нижней до Промежуточной равно 4 × 3 × 2 = 24 км:

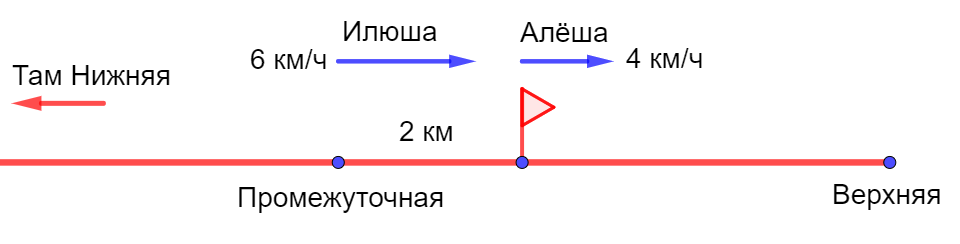
Илюша преодолеет это расстояние за 24 : 6 = 4 часа. В это время Алёша дойдёт до Промежуточной, отдохнёт в ней полчаса и пройдёт за оставшиеся полчаса, пока Илюша добирается до Промежуточной, ещё 2 км. То есть расстояние между Алёшой и Илюшей в момент, когда Илюша дойдёт до Промежуточной, будет равно 2 км:

Скорость их сближения равна 6 – 4 = 2 км/ч. То есть Илюша догонил Алёшу через 2 : 2 = 1 час. В этот момент они встретятся в Верхней. За этот час Илюша успеет отойти от Промежуточной на 6 км, то есть расстояние между Промежуточной и Верхней равно 6 км. То есть общее расстояние между Нижней и Верхней равно 24 + 6 = 30 км.

Ответ: 30 км.

Задание 6. Алёша решил заняться бегом и стал каждое утро выходить к пробежку в парк. Каждый день он пробегал на 400 метров больше, чем в предыдущий день. В результате оказалось, что на шестой день он пробежал в 5 раз больше, чем на первый. Сколько метров Алёша пробежал на третий день?

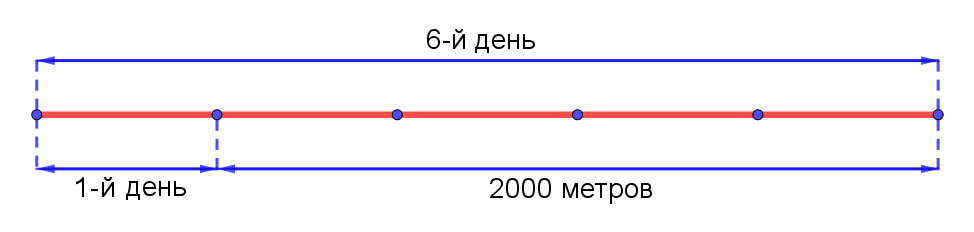
Если Алёша пробегал каждый день на 400 метров больше, чем в предыдущий день, то на шестой день он пробежал на 400 × 5 = 2000 метров больше, чем на первый. Кроме того, по условию известно, что на шестой день Алёша пробежал в 5 раз больше, чем на первый. Изобразим расстояние, которое пробежал Алёша на шестой день, на рисунке:

Видно, что на 2000 метров приходится 4 отрезка, каждый из которых соответствует расстоянию, которое пробежал Алёша в первый день. То есть в первый день Алёша пробежал 2000 : 4 = 500 метров. Тогда на третий день Алёша пробежал: 500 + 400 + 400 = 1300 метров.

Ответ: 1300 метров.

Задание 7. Землекоп роет канаву, а 4 хулигана, закидывая землей, зарывают её обратно. Когда землекоп закончил рыть первую канаву, он обнаружил, что хулиганы успели зарыть её обратно наполовину. Тогда землекоп ушёл рыть такую же точно канаву в другом месте, но начал работать в два раза быстрее. К несчастью для землекопа к группе хулиганов присоединились ещё 2 хулигана, и они продолжили зарывать первую канаву, пока землекоп докапывал вторую. Сколько ещё хулиганов должно присоединиться к группе, чтобы они смогли дозакапывать первую канаву и закапать полностью вторую, пока землекоп роет третью канаву со той же скоростью, с которой он рыл вторую?

Самое сложное в этой задаче: придумать объяснение, которое понятно ученику 4 класса. Но для этого и предназначена подготовка к поступлению в школу 1329 с репетитором. Предлагаю рассуждать следующим образом.

Разобьём мысленно каждую канаву на 8 равных частей. Тогда можно сказать следующее:

1. К моменту, когда землекоп вырыл все 8 частей первой канавы, хулиганы закопали обратно 4 части. Далее землекоп начал копать вторую канаву вдвое быстрее.
2. Если бы хулиганов оставалось 4, то к моменту, когда землекоп закончил бы рыть вторую канаву, хулиганы успели бы закопать ещё 2 части первой канавы (1 часть соответствует работе 2-х хулиганов).
3. Но хулиганов стало на 2 больше, поэтому на самом деле они успели закопать дополнительно не 2, а 3 части первой канавы. То есть 4 + 3 = 7 частей первой канавы оказались закопаны, когда землекоп закончил рыть вторую канаву.
4. Теперь, пока землекоп роет 8 частей третьей канавы со скоростью рытья второй канавы, хулиганы должны зарыть 1 часть первой канавы и 8 частей второй. То есть всего 9 частей. Поскольку 1 часть соответствует работе 2-х хулиганов, то для этого потребуется 9 × 2 = 18 хулиганов.
5. Поскольку 6 хулиганов уже есть, то к группе хулиганов должны присоединиться ещё 18 – 6 = 12 хулиганов.

Ответ: 12.

Задание 8. Маша задумала натуральное число. При делении этого числа на 18 получается число 16 и какое-то положительное число в остатке, а при делении на 16 — число 19 и какое-то положительное число в остатке. Какое число задумала Маша?

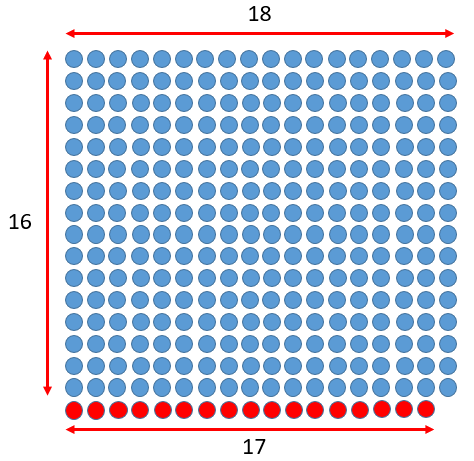
Пусть у нас есть столько фишек, сколько задумала Маша. Тогда мы можем разложить эти фишки в ряды по 18 фишек в каждом. Получится 16 рядов, а один ряд окажется не до конца заполненным. Но сколько же фишек должно быть в этом ряду? Оказывается, что ровно 17, как на рисунке:

Действительно, больше 17 фишек быть не может, так как ряд оказался бы заполненным. Но и меньше 17 быть не может, иначе мы бы не смогли расположить красные фишки в 19-й столбец, так чтобы он оказался заполненным и был бы ещё некоторый остаток. А 19-й столбец должен быть заполненным и сколько-то фишек должно остаться, поскольку по условию при делении задуманного числа на 16 получается число 19 и ещё какой-то положительный остаток.

Осталось только посчитать количество фишек на рисунке. Видно, что полное число фишек равно 16 × 18 + 17 = 305.

Ответ: 305.

Примечание. Если у вас остались какие-то вопросы по решению, посмотрите объяснение в прилагаемом видео. Оно разъяснит вам все детали.

Задание 9. На праздник принесли 1000 конфет. Их нужно раздать 5 мальчикам, которые выстроились в шеренгу. Конфеты раздают мальчикам по одной в следующем порядке: первому — второму — третьему — четвёртому — пятому — четвёртому — третьему — второму — первому — второму — третьем — четвёртому — пятому — четвёртом — третьему — второму — первому — второму … и так далее. Какой мальчик (по счёту) получит последнюю конфету?

Цепочка 1-2-3-4-5-4-3-2, состоящая из 8 цифр, будет повторяться много раз. Чтобы посчитать, сколько именно, нужно поделить 1000 на 8. Получится ровно 125. Значит, эта цепочка повторится 125 раз, после чего конфеты закончатся. А последнюю конфету получит мальчик, чей номер стоит в конце этой цепочки. То есть второй мальчик.

Ответ: второй.

Задание 10. На какое максимальное количество прямоугольников размером 3 × 5 можно разрезать прямоугольник размером 22 × 15? Поясните свой ответ и покажите, как этом можно сделать.

Площадь большого прямоугольника равна 22 × 15 = 330. Площадь маленького прямоугольника равна 3 × 5 = 15. Значит, максимум можно получить 330 : 15 = 22 маленьких прямоугольника. Сделать это можно следующим образом:

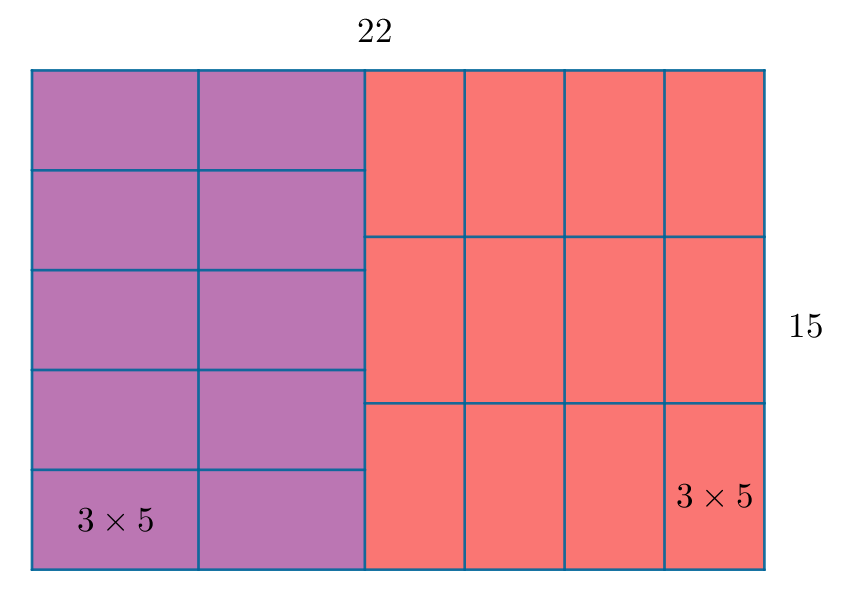
Ответ: 22.

Подготовка к поступлению в школу 1329 с репетитором

Если вам требуется подготовка к вступительному экзамену по математике в школу №1329, обращайтесь к профессиональному репетитору Сергею Валерьевичу. Как показывает опыт, занятия с репетитором — это наиболее эффективный способ подготовки к вступительным экзаменам. Обеспечьте себе поступление в школу 1329 с репетитором. Подробную информацию и преподавателе вы можете найти на этой странице.