Операции с дробями

Четверг, 14 января, 2016

В данной статье репетитором по математике и физике рассказано о том, как производить элементарные операции с обыкновенными дробями: сложение и вычитание, умножение и деление. Рассказано о том, как представить смешанное число в виде неправильной дроби и наоборот, а также о том, как сокращать дроби.

Сложение и вычитание обыкновенных дробей

Чтобы сложить (или вычесть) две обыкновенные дроби нужно:

1) Привести обе дроби к общему знаменателю.

2) Записать результат в виде дроби с числителем, равным сумме числителей исходных дробей, и найденным общим знаменателем.

Напомним, что знаменателем дроби называется число, которое находится снизу, а числителем — число, которое находится сверху от дробной черты. Например, у дроби $\frac{2}{3}$ число $2$ является числителем, а число $3$ — знаменателем.

Общим знаменателем является наименьшее возможное число, которое делится и на знаменатель первой дроби, и на знаменатель второй дроби.

Пример 1. Сложить две дроби: $\frac{2}{33} + \frac{5}{11}$ .

Воспользуемся описанным выше алгоритмом:

1) Наименьшее число, которое делится и на знаменатель первой дроби, и на знаменатель второй дроби, равно $33$ . Это число и будет являться общим знаменателем. Теперь нужно привести обе дроби к общему знаменателю.

С первой дробью ничего делать не нужно, поскольку ее знаменатель уже равен $33$ .
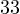Числитель и знаменатель второй дроби нужно умножить на 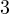$3$ , тогда дробь примет вид: $\frac{15}{33}$ .

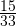2) Складываем полученные дроби: $\frac{2}{33} + \frac{15}{33} = \frac{17}{33}$ .

Умножение обыкновенных дробей

Для умножения двух обыкновенных дробей нужно:

1) Вычислить числитель дроби. Для этого нужно перемножить числители исходных дробей.

2) Вычислить знаменатель дроби. Для этого нужно перемножить знаменатели исходных дробей.

3) Записать полученную дробь.

Иными словами, для всех действительных чисел $a$ , $b$ , $c$ , $d$ $(b\ne 0$ , $d\ne 0)$ справедливо равенство:

$\boxed{ \frac{a}{b}\cdot\frac{c}{d} = \frac{ac}{bd} }$

Пример 2. Перемножить дроби: $\frac{2}{3}\cdot\frac{5}{7}$ .

Для решения данной задачи воспользуемся представленной выше формулой: $\frac{2}{3}\cdot\frac{5}{7} = \frac{2\cdot 5}{3\cdot 7} = \frac{10}{21}$ .

Деление обыкновенных дробей

Чтобы разделить две обыкновенные дроби нужно:

1) Заменить дробь, на которую делим, обратной (грубо говоря, поменять числитель и знаменатель местами).

2) Перемножить полученные дроби.

Иными словами для всех действительных чисел $a$ , $b$ , $c$ , $d$ $(b\ne 0$ , $c\ne 0$ , $d\ne 0)$ справедливо равенство:

$\boxed{ \frac{a}{b}:\frac{c}{d} = \frac{a}{b}\cdot\frac{d}{c} = \frac{ad}{bc} }$

Пример 3. Разделите дроби: $\frac{3}{8}:\frac{2}{5}$ .

Для решения этой задачи воспользуемся приведенной выше формулой: $\frac{3}{8}:\frac{2}{5}=\frac{3}{8}\cdot\frac{5}{2}=\frac{15}{16}$ .

Представление смешанного числа в виде неправильной дроби

Разберемся теперь, как быть, если требуется выполнить какую-либо операцию с дробями, представленными в виде смешанных чисел. В этом случае сперва нужно представить смешанные числа в виде неправильных дробей, а затем выполнить необходимую операцию.

Напомним, что неправильной называется дробь, у которой числитель больше или равен знаменателю.

Напомним также, что у смешанного числа есть дробная часть и целая часть. Например, у смешанного числа $2\frac{4}{5}$ дробная часть равна $\frac{4}{5}$ , а целая часть равна $2$ .

Чтобы представить смешанное число в виде неправильной дроби нужно:

1) Вычислить числитель неправильной дроби. Для этого нужно умножить знаменатель дробной части смешанного числа на его целую часть, после чего к полученному результату прибавить числитель дробной части.

2) Записать неправильную дробь с полученным числителем и знаменателем, равным знаменателю дробной части смешанного числа.

Пример 4. Представить смешанное число $1\frac{4}{7}$ в виде неправильной дроби.

Воспользуемся представленным выше алгоритмом: $1\frac{4}{7} = \frac{7\cdot 1 + 4}{7} = \frac{11}{7}$ .

Чтобы представить неправильную дробь в виде смешанного числа нужно:

1) Разделить с остатком числитель неправильной дроби на ее знаменатель.

2) Неполное частное от деления будет являться целой частью смешанного числа, остаток — числителем дробной части смешанного числа, а ее знаменатель будет равен знаменателю исходной неправильной дроби.

3) Записать полученное смешанное число.

Пример 5. Представьте неправильную дробь $\frac{65}{7}$ в виде смешанного числа.

Воспользуемся описанным выше алгоритмом. Неполное частное от деления $65$ на $7$ равна $9$ , а остаток от деления равен $2$ . Следовательно, искомое смешанное число равно $9\frac{2}{7}$ .

Сокращение дробей

Результатом выполнения операций с дробями может оказать дробь, числитель и знаменатель которой имеют общие делители. Такую дробь нужно сократить, то есть разделать числитель и знаменатель на наибольший общий делитель.

Напомним, что наибольшим общим делителем называется наибольшее число из возможных, на которое без остатка делится и числитель, и знаменатель.

Пример 6. Сократите дробь: $\frac{24}{42}$ .

Наибольшим общим делителем чисел $24$ и $42$ является число $6$ . Следовательно, после сокращения дробь принимает вид: $\frac{24}{42} = \frac{4\cdot 6}{7\cdot 6} = \frac{4}{7}$ .