 Лицей № 1580 при МТГУ имени Н.Э. Баумана — это одно из достаточно сильных образовательных учреждений для школьников в Москве в плане преподавания физики и математики. Многие родители хотят, чтобы их дети поступили именно туда. Но сделать это не так просто, ведь при поступлении предполагается сдача обязательного экзамена, сложность которого достаточно велика. Предлагаю вашему вниманию разбор типового варианта вступительного экзамена в лицей 1580 по математике, который предлагалось выполнить абитуриентам для поступления в 9 класс.
Лицей № 1580 при МТГУ имени Н.Э. Баумана — это одно из достаточно сильных образовательных учреждений для школьников в Москве в плане преподавания физики и математики. Многие родители хотят, чтобы их дети поступили именно туда. Но сделать это не так просто, ведь при поступлении предполагается сдача обязательного экзамена, сложность которого достаточно велика. Предлагаю вашему вниманию разбор типового варианта вступительного экзамена в лицей 1580 по математике, который предлагалось выполнить абитуриентам для поступления в 9 класс.
| 1. Решите уравнение: |
Первый корень легко угадывается: ![]() . Второй корень можно найти с помощью теоремы Виета. Учитывая, что
. Второй корень можно найти с помощью теоремы Виета. Учитывая, что ![]() , получаем
, получаем ![]() .
.
| 2. Упростите выражение:
|
![]()
| 3. Вычислите значения выражения:
|
Умножим числитель и знаменатель каждой дроби на сопряжённое со знаменателем выражение и воспользуемся формулой «разность квадратов»:
![Rendered by QuickLaTeX.com \[ \frac{1}{\sqrt{7}-\sqrt{6}} = \frac{\sqrt{7}+\sqrt{6}}{(\sqrt{7}-\sqrt{6})(\sqrt{7}+\sqrt{6})} = \sqrt{7}+\sqrt{6} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-63b3c7550fb6df1e3c720f6abe109563_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{3}{\sqrt{6}-\sqrt{3}} = \frac{3(\sqrt{6}+\sqrt{3})}{(\sqrt{6}-\sqrt{3})(\sqrt{6}+\sqrt{3})} = \sqrt{6}+\sqrt{3} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f9c7cdbb261115f0d4efe309d13c0096_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{4}{\sqrt{7}+\sqrt{3}} = \frac{4(\sqrt{7}-\sqrt{3})}{(\sqrt{7}-\sqrt{3})(\sqrt{7}+\sqrt{3})} = \sqrt{7}-\sqrt{3}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5387134af30891834fde989fb2a0f063_l3.png)
В результате получаем ответ:
![]()
| 4. Удвоенная разность корней квадратного уравнения |
Пусть ![]() и
и ![]() — корни квадратного уравнения
— корни квадратного уравнения ![]() . Тогда по теореме Виета имеем:
. Тогда по теореме Виета имеем: ![]() . Кроме того, по условию
. Кроме того, по условию ![]() . То есть имеет место система:
. То есть имеет место система:
![Rendered by QuickLaTeX.com \[ \begin{cases} x_1+x_2 = 18 \\ 2(x_1-x_2) = 8 \end{cases}\Leftrightarrow \begin{cases} x_1 = 11 \\ x_2 = 7 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-54aac5ef6f584cbbaa140ce226145768_l3.png)
Кроме того, по теореме Виета имеем: ![]() .
.
| 5. Упростите выражение на области допустимых значений:
|
Используя формулу «разность кубов», упрощаем сперва выражение, стоящее в скобках:
![]()
![Rendered by QuickLaTeX.com \[ = \frac{x^2-4-6x+13}{(x-2)(x^2+2x+4)} = \frac{(x-3)^2}{(x-2)(x^2+2x+4)}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4da1cffbf71a9226028ab6d29e424d1c_l3.png)
Упрощаем дальше:
![Rendered by QuickLaTeX.com \[ \frac{(3-x)^2}{(x-2)(x^2+2x+4)}\cdot\frac{2(x^2+2x+4)}{3-x}\cdot(x-2) = \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e1ba94c83d6c6b55df8ae1e0f9035bf9_l3.png)
![]()
| 6. В равнобедренной трапеции боковая сторона равна 10 см, диагональ — 17 см, а разность оснований — 12 см. Найдите площадь трапеции. |
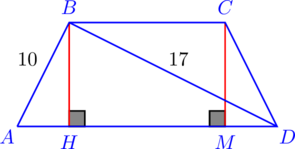
Пусть ![]() и
и ![]() . Тогда по условию
. Тогда по условию ![]() . Поскольку трапеция равнобедренная,
. Поскольку трапеция равнобедренная, ![]() . Тогда по теореме Пифагора
. Тогда по теореме Пифагора ![]() . Также из теоремы Пифагора для треугольника
. Также из теоремы Пифагора для треугольника ![]() получаем, что
получаем, что ![]() . Поскольку трапеция равнобедренная,
. Поскольку трапеция равнобедренная, ![]() Следовательно, искомая площадь трапеции равна
Следовательно, искомая площадь трапеции равна ![]() .
.
| 7. Высота, проведенная из вершины прямого угла прямоугольного треугольника, равна 6 см и дели гипотенузу на отрезки, один из которых больше другого на 5 см. Найдите стороны треугольника. |
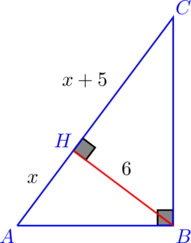
Пусть ![]() , тогда получаем, что
, тогда получаем, что ![]() , и
, и ![]() . Значит, треугольники
. Значит, треугольники ![]() и
и ![]() подобны по двум углам (так как
подобны по двум углам (так как ![]() ,
, ![]() ). Используя это подобие, получаем:
). Используя это подобие, получаем:
![]()
В пропорции произведение крайних членов равно произведению средних, поэтому получаем:
(1) ![]()
Из последнего уравнения получаем положительный корень ![]() . Тогда, используя теорему Пифагора, находим все стороны треугольника
. Тогда, используя теорему Пифагора, находим все стороны треугольника ![]() . Получаем, что они равны
. Получаем, что они равны ![]() ,
, ![]() и
и ![]() .
.
Примечание. Уравнение (1), конечно, можно было записать сразу, сославшись на теорему о пропорциональных отрезках в прямоугольном треугольнике. Однако, опыт показывает, что не все школьники помнят об этой теореме и знают, как её доказывать.
| 8. В треугольнике со сторонами 15 см, 15 см и 24 см найдите расстояния от точки пересечения медиан до сторон треугольника. |
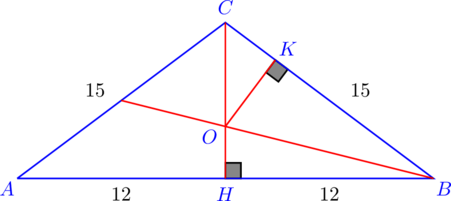
Треугольник ![]() — равнобедренный, поэтому медиана
— равнобедренный, поэтому медиана ![]() , проведенная к его основанию
, проведенная к его основанию ![]() , является также и высотой. Из теоремы Пифагора для треугольника
, является также и высотой. Из теоремы Пифагора для треугольника ![]() находим
находим ![]() .
.
Медианы треугольника точкой пересечения делятся в отношении 2 к 1, считая от вершины, следовательно, расстояние от точки пересечения медиан до стороны ![]() равно
равно ![]() .
.
Из треугольника ![]() получаем
получаем ![]() . Тогда из треугольника
. Тогда из треугольника ![]() получаем
получаем ![]() .
.
Телефон репетитора по математике для подготовки к вступительному экзамену в лицей 1580, Сергея Валерьевича

![Rendered by QuickLaTeX.com \[ \left(\frac{x+2}{x^2+2x+4}-\frac{6x-13}{x^3-8}\right)\cdot\frac{2x^2+4x+8}{3-x}\cdot(x-2). \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-79c51adfcac7dbdcaafa27f6b3d1a161_l3.png)