Лайфхак для решения заданий теста в лицей ВШЭ

В этой статье я поделюсь с вами одним очень полезным методом, то есть таким лайфхаком, который поможет вам быстро и легко решать некоторые задания из комплексного вступительного теста в лицей Высшей школы экономики. Разберём мы его на примере решения задания одного из демонстрационных вариантов, выложенных на сайте лицея.

Если вам требуется подготовка к поступлению в лицей Высшей школы экономики, вы можете обратиться ко мне. Я являюсь профессиональным репетитором и имею большой успешный опыт в этом деле. Мои контакты вы сможете найти на этой странице. Также совсем недавно я запустил свой новый сайт cleverfox.info, где представлены тренировочные варианты вступительных экзаменов по математике в лицей ВШЭ с моими авторскими подробными решениями всех заданий. Это отличный вариант для самостоятельной подготовки. 

Найдите наибольшее решение неравенства

Как видите, неравенство в условии иррациональное. То есть содержит корень. Из своего опыта могу сказать, что многие школьники, когда видят такое неравенство, начинают честно его решать. Возводят обе части в квадрат, пишут какие-то дополнительные условия, приводят подобные слагаемые, решают получившееся квадратичное неравенство. И если они не делают никаких ошибок по дороге, то получают в конце концов правильное решение, потратив, правда, при этом уйму времени и сил. Но в большинстве случаев они делают где-то ошибку из-за невнимательности и просто получают неправильный ответ. Поэтому на таком решении можно смело ставить жирный крест!

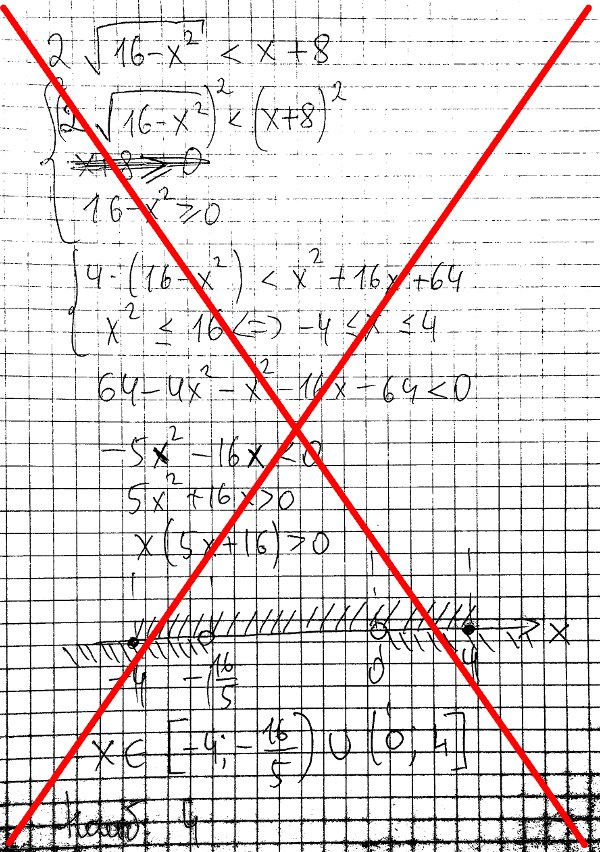
Ничего этого здесь не нужно! А нужно следующее. Здесь то как раз и появляется тот самый полезный лайфхак. Нас же просят найти наибольшее решение этого неравенства. Ну так давайте сперва найдём, какие в принципе значения переменной мы можем подставить в это неравенство.

Дело в том, что здесь есть корень. А он имеет смысл далеко не всегда, а только в том случае, если подкоренное выражение неотрицательно. То есть при . Данное неравенство эквивалентно неравенству , которое выполняется при любом значении из промежутка .

Что же мы получили? А получили мы то, что никакое число бОльшее 4 мы даже в принципе не можем подставить в это неравенство. Поэтому если так вдруг окажется, что число 4 является решением этого неравенства, то бОльшего решения у этого неравенства уже точно не будет. Ну а в том, что число 4 является решением этого неравенства, можно легко убедиться прямой подстановкой. Если я поставлю в исходное неравенство, то слева получится 0, а справа 12. В итоге мы получим верное неравенство .

Итак, наибольшим решением неравенства является число 4. И как видите, мы быстро и легко получили этот правильный ответ даже без решения самого неравенства.

Вот такой вот очень простой лайфхак. Чтобы успешно сдать вступительные экзамены в лицей ВШЭ, нужно такими эффективными методами очень хорошо владеть. И в изучении этих методов вам лучше всего поможет мой новый сайт cleverfox.info.

На этом сайте вложено большое количество вариантов тестов для поступления в лицей ВШЭ с подобным разбором от профессионального репетитора. Можно тренироваться самостоятельно. Сперва пытаться решать задания самому, а затем сравнивать свои решения с теми, которые представлены на сайте. Доступ к нескольким вариантам тестов абсолютно бесплатный. Пройдите короткую регистрацию и приступите к решению тестов уже сейчас. Ну а если вам понравится, можно в пару кликов приобрести подписку и сразу же начать полноценную подготовку к вступительному экзамену в лицей ВШЭ.

Ну а также я сам готовлю школьников к поступлению в лицей НИУ ВШЭ. Имею в этом деле обширный успешный опыт. Так что если вам требуется подготовка к вступительным экзаменам в лицей Высшей школы экономики, я готов её организовать. Мои контакты вы сможете найти на этой странице.

Успехов!

Сергей Валерьевич