В данной статье рассмотрено решение интересной задачи с кубиками из вступительного экзамена в 5 класс школы №1543 (бывшее название «Гимназия 1543 на Юго-западе»). Подобные задачи встречались также на вступительных экзаменах в ряд других школ, например, во «Вторую школу». Так что эта статья может оказать полезной для всех, кто готовиться к вступительным экзаменам в ведущие математические школы Москвы и других городов.
|
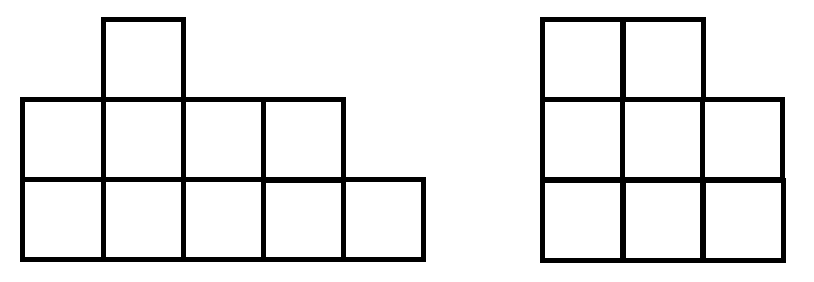
У Димы есть площадка 3 × 5, на которую он поставил несколько кубиков с ребром 1. На рисунках даны виды спереди и сбоку того, что получилось. Какое наименьшее число кубиков мог поставить Дима?
|
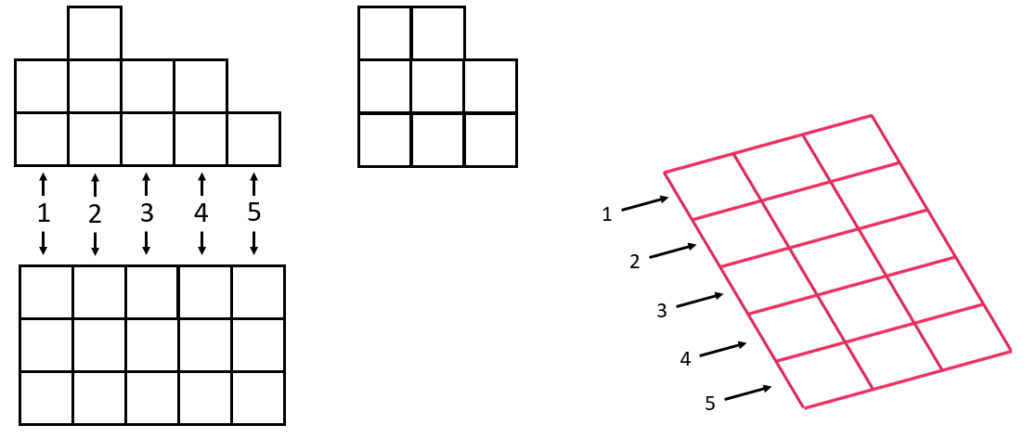
- Пронумеруем слои нашей фигуры.
- Нарисуем площадку, которую Дима застраивает кубиками. Получится как бы вид сверху. В клетках этого вида будем записывать цифрами, сколько кубиков Дима мог поставить на каждую из них.
- Справа будем рисовать, как это выглядит в реальности. Нумерация слоёв на правом рисунке будет такой же, как и на всех остальных рисунках.
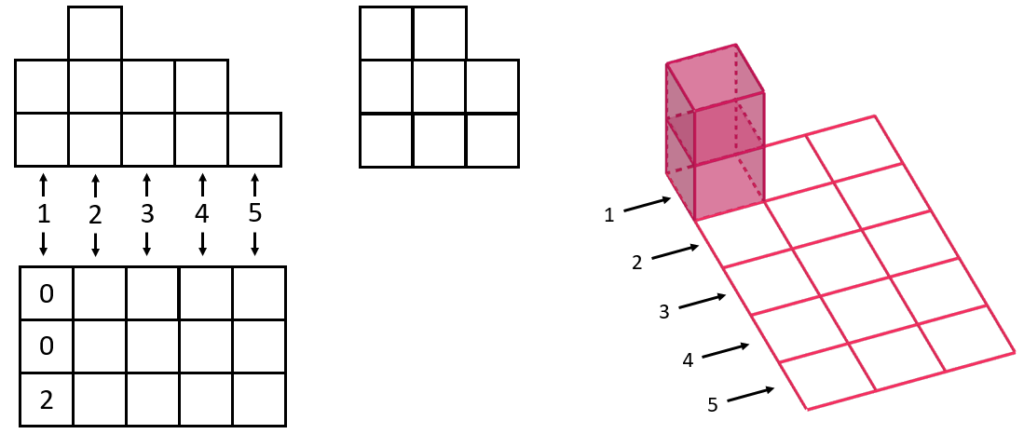
Рассмотрим сперва первый слой. В нём есть два кубика. Причём верхний кубик обязательно должен стоять на нижнем. То есть это получается столбик из двух кубиков. В задаче требуется сделать так, чтобы кубиков в конструкции было минимальное количество. Ну а поскольку в первом слое меньше двух, как мы выяснили, сделать нельзя, то постараемся сделать так, чтобы их было ровно два. Вопрос в том, где этот столбик из двух кубиков расположить? Понятно, что сбоку. Почему? Да потому что на рисунке сбоку у нас тоже есть этот столбик из двух кубиков. И расположен он именно сбоку. Тогда на двух клетках первого слоя у нас не будет ни одного кубика, а на третьей их будет два.
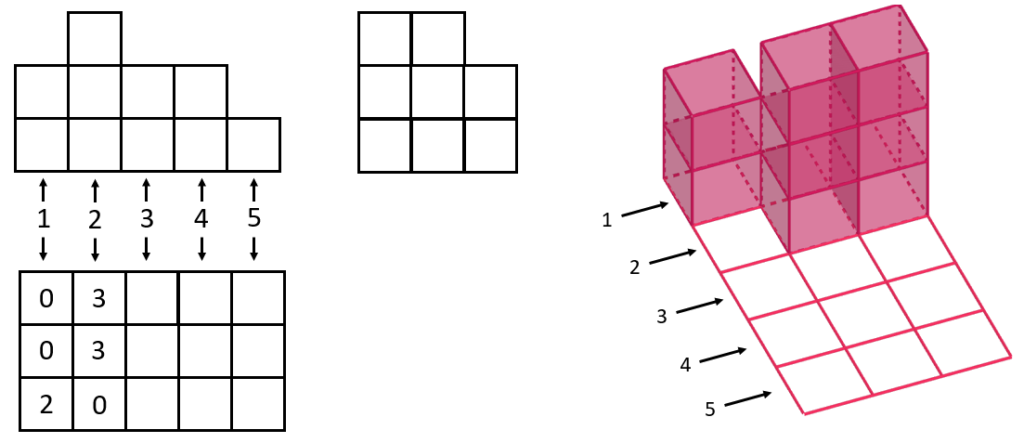
Перейдём теперь ко второму слою. В этом слое у нас уже находится столбик из трёх кубиков. Опять же, эти кубики должны обязательно стоять друг на друге. Ну а если посмотреть снова на вид сбоку, то мы увидим, что таких столбиков из трёх кубиков будет в этом слое целых два! Именно в этом втором слое, потому что ни в каком другом слое на виде спереди мы таких столбиков больше не видим. Итак, во втором слое у нас ноль кубиков на нижней клеточке, а на двух других по три кубика. Три в одном столбике, и три в другом.
Теперь переходим к третьему слою. Здесь у нас знакомая ситуация. Столбик из двух кубиков. Его мы поставим на краю. А на остальных клетках этого слоя кубиков не будет. Интересно заметить, что здесь мы не обязаны были ставить этот столбик именно на краю. Можно было бы поставить его и по центру. На вид спереди это никак бы не повлияло, так как кубики, которые мы уже поставили, загораживают нам весь этот вид. Но поскольку на общее количество кубиков это никак не влияет (их всё равно будет ровно два в этом слое), то для определённости поставим эти кубики на краю.
Точно такая же ситуация у нас и с четвёртым слоем. Поставим столбик из двух кубиков здесь вновь на краю. А в остальных клеточках будут нули. Ну а в последнем пятом слое у нас только один кубик. Его мы снова, по традиции, можем поставить на краю. Давайте поставим. Хотя, подчеркнём ещё раз, это вовсе не обязательно. Можно было бы поставить его и по центру. Это без разницы. На остальных клетках этого слоя кубиков не будет вовсе.
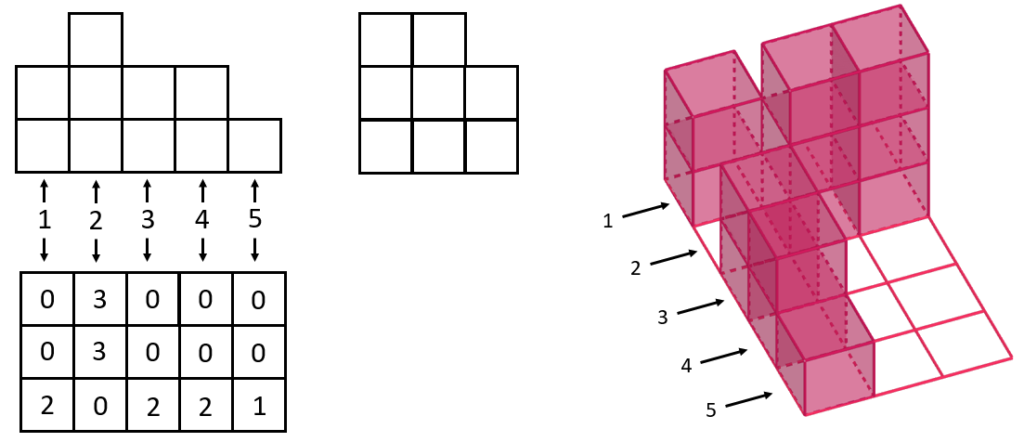
Вот и получилась полная картина, как эти кубики могут быть расставлен. И мы показали, что это минимальное количество кубиков. Меньшим количеством кубиков уже не обойтись, потому что если убрать хотя бы один из кубиков, то либо какой-нибудь столбик развалится, либо виды спереди и сбоку уже будут не такими, как на приведённых в условии рисунках.
Вот такая задача из вступительного экзамена по математике в 5 класс школы 1543. Официально её теперь называют школой, хотя многие её, конечно, знают в первую очередь как гимназию. Ну и я на протяжении уже многих лет занимаюсь подготовкой школьников к вступительным экзаменам в эту гимназию. Имею в этом деле большой и успешный опыт. Так что если вам нужна подготовка к вступительным экзаменам в школу 1543, я с удовольствием вам помогу. Я являюсь профессиональным репетитором по математике и физике . Мои контакты вы можете найти на этой странице.
Успехов и всего доброго!