Из заданий интернет-олимпиады Высшей школы экономики по математике, прошедшей 22 января 2012 года, наибольший интерес вызвала задача под номером 10. Назовем ее задачей «о количестве ломаных в кубе». Как я ни старался, найти готовое решение в интернете мне не удалось. «Google Вопросы и ответы» на пару с «Ответы@Mail.ru» упорно дают лишь формулировку без решения, как в общем и другие репетиторы, предпочитающие размещать в своих блогах ни к чему не обязывающие указания и комментарии вместо подробных решений олимпиадных задач. Поэтому, уверенный, что я не изобретаю велосипед, приведу здесь текст решения.
Задача. Сколько ломаных длины 7, проходящих через все вершины, можно образовать из ребер единичного куба?
Решение: итак, требуется найти все такие ломаные, которые проходили бы через все вершины данного куба и состояли из его ребер. Очевидно, что каждая такая ломаная не будет являться замкнутой и нигде не будет пересекать саму себя. Действительно, если предположить обратное, то одна грань куба содержит четыре отрезка ломаной, тогда оставшимися тремя отрезками четыре оставшиеся вершины куба не обойти.
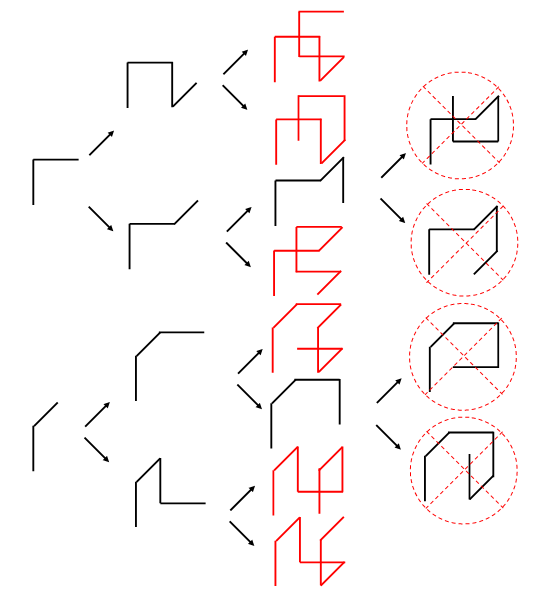
Следуя этой логике, можно нарисовать все возможные варианты искомых ломаных, которые можно провести для каждого ребра куба:
Ломаные, которые можно провести для каждого ребра куба
Итого шесть возможных вариантов. Важно обратить внимание, что конечные ребра ломаных всегда разные, то есть два любых ребра куба соединяются только одной ломаной! Всего в кубе двенадцать ребер, поэтому всего ломаных: шесть × двенадцать = семьдесят два, но каждую ломаную мы посчитали два раза, поскольку прошлись по всем ребрам куба, поэтому окончательный ответ: семьдесят два ÷ два = тридцать шесть.
Ответ: 36.
Оставляем комментарии, присылаем интересные олимпиадные задачи, учимся решать их самостоятельно!
Ваш репетитор по физике и математике
Сергей Валерьевич
Добавить комментарий