Вступительный экзамен в школу 109 (математика)

Автор

Воскресенье, 23 июля, 2017

Школа №109 в Москве

В статье представлен разбор вступительного экзамена по математике в школу №109 г. Москвы. Если вам требуется подготовка к поступлению в эту школу, рекомендуем обратиться к профессиональному репетитору по математике и физике. Место проведения занятий находится недалеко от школы 109.  При этом возможны как очные, так и дистанционные занятия по подготовке в вступительному экзамену.

Разбор вступительного экзамена по математике в школу №109

1. Упростите выражение:

    \[ \left(\frac{1}{2-4\sqrt{x}}+\frac{\sqrt{x}+1}{\left(2\sqrt{x}\right)^3-1}\cdot\frac{4x+2\sqrt{x}+1}{1+2\sqrt{x}}\right):\frac{1}{4\sqrt{x}-2}. \]

Область допустимых значений данного выражения содержит все числа, за исключением x=\frac{1}{4}. С учётом замены a=\sqrt{x}, разложения на множители и сокращения везде, где это возможно, получаем следующее выражение:

    \[ \left(\frac{1}{2(1-2a)}+\frac{a+1}{(2a-1)}\cdot\frac{1}{1+2a}\right):\frac{1}{2(2a-1)}. \]

Сейчас удобнее раскрыть скобки. При этом с учётом правила деления дробей, возвращаясь к исходной переменной, получаем следующее выражение:

    \[ -1+\frac{2(a+1)}{1+2a}=\frac{1}{1+2a} = \frac{1}{1+2\sqrt{x}}. \]

2. При каком значении k сумма корней уравнения

    \[ x^2+(k^2-5k-6)x-k+3=0 \]

равна 0?

По теореме Виета сумма корней приведённого квадратного уравнения равна коэффициенту b, взятому с противоположным знаком. То есть в данному случае k^2-5k-6 = 0, то есть k_1=6 и k_2=-1.

3. Найдите (x;y) из уравнения:

    \[ \left(\frac{1}{x}+\frac{1}{y}-\frac{3}{8}\right)^2+(x+y-12)^2=0. \]

Сумма квадратов двух выражений равна нулю тогда и только тогда, когда оба выражения одновременно обращаются в нуль. То есть исходное уравнение равносильно следующей системе уравнений:

    \[ \begin{cases} \frac{1}{x}+\frac{1}{y}-\frac{3}{8} = 0\\ x+y-12 = 0. \end{cases} \]

Из второго уравнения системы получаем x=12-y. Подставляем это в первое уравнение и решаем полученное уравнение:

    \[ \frac{1}{12-y}+\frac{1}{y}-\frac{3}{8} = 0\Leftrightarrow \]

    \[ \frac{8}{12-y}+\frac{8}{y}= 3\Leftrightarrow \]

    \[ \frac{8y+96-8y}{y(12-y)}=3\Leftrightarrow \frac{96}{y(12-y)}=3. \]

Для y≠12 и y≠0 получаем квадратное уравнение y2-12y+32=0, из которого находим y1=8 и y2=4. Тогда x1=4 и x2=8. Итак, ответ (4;8) и (8;4).

4. При каком m уравнение

    \[ m=3+\frac{(x+6)^2}{\sqrt{(x+6)^2}} \]

не имеет решений?

Область допустимых значений данного уравнения включает все значения x, кроме x=-6. Используя правила преобразования выражений, содержащих корни, упрощаем исходное уравнение в области допустимых значений к следующему виду:

    \[ m=3+\frac{|x+6|^2}{|x+6|} = 3+|x+6|. \]

Выражение |x+6| при x≠-6 принимает любые положительные значения. Значит, область значений выражения 3+|x+6| задаётся промежутком (3;+∞). То есть при любых m≤3 исходное уравнение не будет иметь решений.

5. Доказать, что при любом целом a выражение 5a2+13a−30 делится на 6.

Это утверждение неверно. Приведём контрпример. При a=5 значение выражения равно 160, что не делится на 6. Но как прийти к этому контрпримеру?

Так как число 30 делится на 6, то пытаемся доказать, что 5a2+13a делится на 6. Для этого проверим делимость этого выражения на 2 и на 3.

Проверяем делимость на 2. Возможны два случая:

  1. Если a — чётное число, то есть a=2n, n∈Z, то выражение принимает вид 20n2+26n, которое делится на 2.
  2. Если a — нечётное число, то есть a=2n+1, n∈Z, то выражение принимает вид 20n2+46n+18, которое также делится на 2.

Проверяем делимость на 3. Возможны три случая:

  1. Если a=3n, n∈Z, то выражение принимает вид 45n2+39n, которое делится на 3.
  2. Если a=3n+1, n∈Z, то выражение принимает вид 45n2+69n+18, которое также делится на 3.
  3. Если a=3n+2, n∈Z, то выражение принимает вид 45n2+99n+46, которое не делится на 3, так как 46 не делится на 3.

Итак, достаточно взять, например, n=1 и привести уже описанный в начале решения контрпример с a=5.

6. Две машины, работая вместе, могут очистить от снега определённую площадь за 12 часов. Если бы сначала первая машина выполнила половину работы, а затем вторая закончила бы уборку, то на всю работу ушло бы 25 часов. За сколько часов может каждая машина очистить от снега эту площадь, работая отдельно.

Введём обозначения, выраженные в условных единицах. Возьмём «определённую площадь» за 1. Пусть производительность первой машины равна x, а производительность второй машины равна y. Тогда из условия получаем следующую систему уравнений:

    \[ \begin{cases} \frac{1}{x+y}=12\\ \frac{1}{2x}+\frac{1}{2y}=25. \end{cases} \]

Из этой системы находим, что x=\frac{1}{30} и y=\frac{1}{20}. То есть первая машина может в одиночку очистить всю площадь за 30 часов, а вторая — за 20.

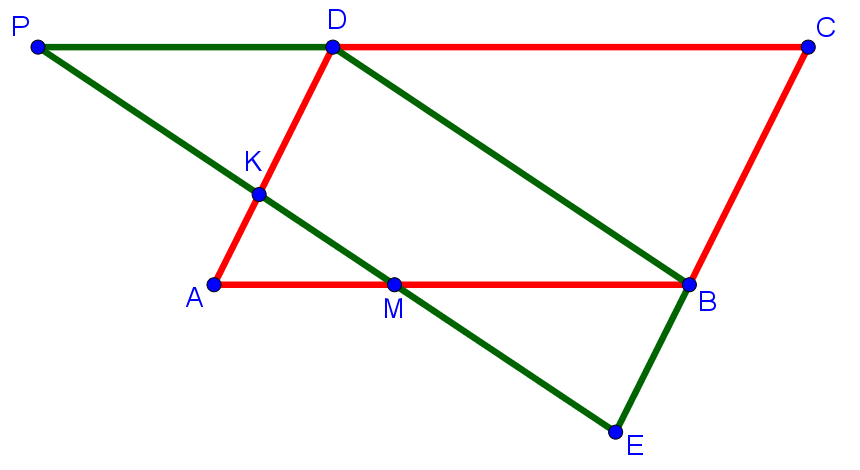
7. На сторонах AB и AD параллелограмма ABCD взяты точки M и K соответственно. Прямая MK параллельна прямой BD. Прямая MK пересекает луч CB в точке E, а луч CD в точке P. Докажите, что EM = KP.

Рисунок к задаче по геометрии из вступительного экзамена по математике в школу 109

Так как ABCD — параллелограмм, то ∠ADC = ∠ABC. Значит, ∠PDK = ∠MBE, так как в сумме с ∠ADC и ∠ABC, соответственно, они образуют развёрнутые углы. Так как PDBM — параллелограмм, то PD = MB. Так как KDBE — параллелограмм, то KD = BE. Значит, ΔPDK = ΔMBE по двум сторонам и углу между ними. Значит, PK = ME. Что и требовалось доказать.

Если вам требуется подготовка к вступительному экзамену в школу №109, обращайтесь к профессиональному репетитору по математике и физике в Тропарёво, Сергею Валерьевичу. Возможны очные и дистанционные занятия.

Метки: , ,
Опубликовано в категории Методическая копилка | Нет комментариев »

Добавить комментарий