В данной статье репетитор по математике рассказывает о простом и эффективном способе составления уравнения параболы по её графику, которому вас не научат в школе. Дочитайте эту статью до конца или посмотрите видео с подробным объяснением, потому что эта информация может вам пригодиться на экзамене.
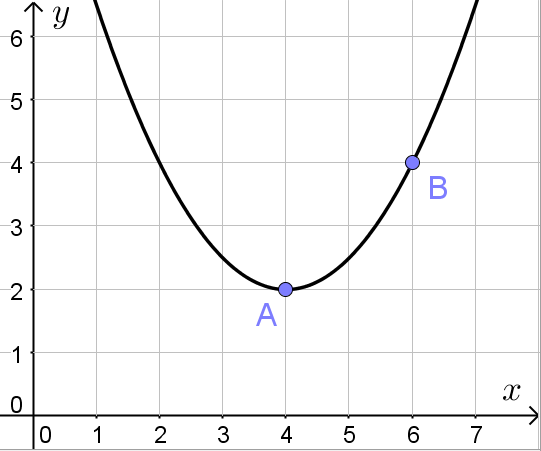
Задача состоит в том, чтобы по графику параболы (см. рисунок) определить коэффициенты a, b и c соответствующей квадратичной функции 
:
Существует стандартный и крайне неэффективный способ решения этой задачи. Он заключается в том, чтобы через координату 
вершины параболы связать коэффициенты a и b, используя формулу 
. Затем взять координаты двух точек, которые принадлежат параболе, составить систему уравнений и решить её относительно искомых коэффициентов. Считать придётся долго и муторно.
Мы не пойдём этим путём. Предлагаемый в данной статье способ намного более прост и изящен. Введём новую систему координат 
с центром в вершине параболы и осями, сонаправленными с исходной системой координат. В данной системе координат уравнение нашей параболы будет иметь вид: 
, где 
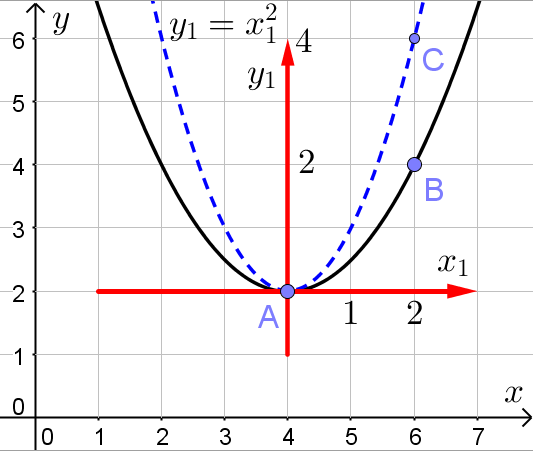
. Изобразим в новой системе координат график квадратичной функции 
(синяя пунктирная линия на рисунке):
Абсциссы точек C и B в новой системе координат равны. Ордината точки C в 2 раза больше ординаты точки B. Значит график исходной параболы в новой системе координат получен умножением на 
всех ординат точек графика функции 
. Откуда получаем, что 
. Значит исходная парабола может быть представлена в виде следующего выражения в новой системе координат: 
.
Осталось перейти в исходную систему координат. Поскольку новая система координат получена путём параллельного переноса исходной системы координат на 4 единичных отрезка вправо и 2 единичных отрезка вверх, то в исходной системе координат наша парабола может быть представлена в виде следующего выражения:
![\[ y = \frac{1}{2}(x-4)^2+2 = \frac{1}{2}x^2-4x+10. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e7cec75d95818cca2330023c1ec246b7_l3.png "Rendered by QuickLaTeX.com")
Как видите, данный способ требует минимум вычислений и фактически является полуустным. Запомните этот способ, он может пригодиться вам при решений задач из ЕГЭ, ОГЭ или вступительных экзаменов в вузы и школы с углубленным изучением математики.
Статья написана репетитором по математике в Москве, Сергеем Валерьевичем
Почему Вы говорите, что этому способу не научат в школе? Нас вот учили.
А Вы в какой школе учились?
Класс был с физико-математическим профилем, но школа обычная, общеобразовательная.
Ну я про все школы говорить не могу, но это всё же положительное исключение, а не правило. Вам, видимо, повезло с школой:-)
А вот мне нет
Что именно не понятно?
Можете рассказать как посторить график функции и определить при каких значениях прямая имеет с графиком одну общую точку?
Так обычно формулируются задачи с параметрами. Про них на сайте есть отдельная статья.
А если вершина параболы не в целочисленных координатах, тогда как быть?
Поскольку задание формулируется так, что нужно найти уравнение параболы из графика, то предполагается, что все необходимые координаты можно найти из этого графика. Например, в этом случае график может быть нарисован на миллиметровой бумаге. Ну а сам алгоритм решения будет абсолютно аналогичным.
Сергей, спасибо. 15 минут бился над плавным приближением к географическому объекту на карте с большой высоты. Нужны были коэффициенты для формулы изменения масштаба. Глянул на Ваш рисунок, и всё прояснилось.
Вот этого не ожидал, если честно:) Чтобы мои статьи помогли кому-то в решении таких сложных задач). Рад, что статья оказалась для Вас полезной.
Хотел выложить видео, чтобы не быть голословным и показать, что всё это может пригодиться не только в школе, но защита от спама не пропускает.
Можете прислать видео или ссылку на него на seliverstov@yourtutor.info? Я прикреплю её к Вашему комментарию.
А если ветви функции направлены вниз? то нахождение А и B C не правильно ? по сдвигу ? Просто у меня не получается найти A. При A больше нуля все совпадает но при ее переворачивании функция уходит в другие значения.
Если ветви направлены вниз, алгоритм не меняется. Всё то же самое. Коэффициент A будет получаться отрицательным.
Сергей, здравствуйте. И все-таки в сборнике 3000 задач для подготовке к ОГЭ (ГИА) за 2015 год , например, 1460 , для определения а приведен график, где непонятно даже положение вершины, то ли посередине, то ли нет, и таких задач несколько Как быть? Заранее спасибо.
Так и хочется как-нибудь применить этот способ для составления уравнения параболы по трем заданным точкам.
Скажи как найти y вершини(с=0)
Здравствуйте, вы не могли бы помочь. Год назад я каким-то образом формулу графика параболы ax2+bx+c переделывал в формулу m(x+n)2+v
(Переменные во втором выражении я поставил наугад)
Сейчас не могу вспомнить. В интернете не нашёл. Помогите, буду благодарен
2 это квадрат
пожалуйста, помогите не могу понять как это сделать вообщем надо составить формулу параболы условия такие она точно отрицательная
с ветвями вниз и по х 0т нуля до 10 а по у то вершина 140 по у
Не совсем ясно, никак до конца не разберусь, помогите кто в теме. Вот парабола ветви направлены вниз и…
Две окружн х²+(у-1)²=1 и х²+(у+4)²=16 касаются в точке М{0,0}. Увеличивая радиус окружн каждый раз на определён величину я строил концентр окружн и получил соотвествено точки пересечения.Я соеденил эти точки линией и получил кривую 2-го порядка. Незнаю как по известным уже координ[х,у] составитьуравн и определить тип кривой (парабола или гипербола) буду благодарен в помощи и обьяснении) Анатолий
Спасибо вам
Действительно легче