
В данной статье разобраны примеры заданий отборочного тура олимпиады «Высшая проба» по математике для 9 класса за 2019 год. Данные задачи меня попросили решить мои ученики, поэтому их всего 3. Полного варианта, к сожалению, у меня нет. Если у вас есть другие, пишите условия в комментариях. Будем их решать и добавлять решения в статью.
Решение задач отборочного тура олимпиады «Высшая проба»
| Пример 1. В треугольнике ABC сторона |
Изобразим ситуацию на рисунке вместе с некоторыми дополнительными построениями:
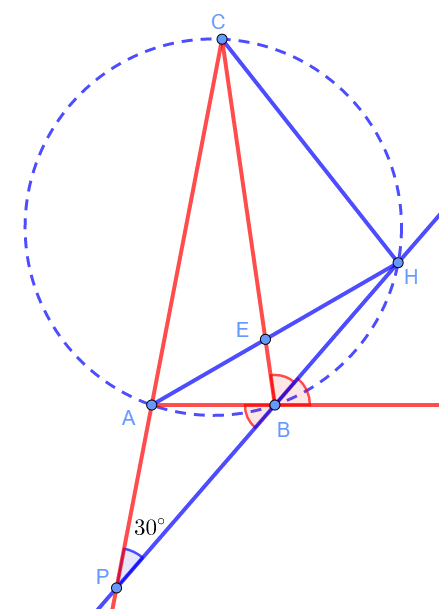
Дополнительно описали окружность вокруг треугольника ABC. Прямая, содержащая биссектрису внешнего угла B, пересекла эту окружность в точке H. Заметим, что ∠CAB + ∠CHB = 180°, но и ∠CAB + ∠PAB = 180°. Значит, ∠PAB = ∠CHB. Значит, треугольники CHB и PAB подобны по двум углам, поэтому ∠BCH = ∠APB = 30°. Заметим также, что ∠HAB = ∠BCH = 30°, так эти вписанные углы опираются на одну дугу.
Введём дополнительные обозначения. Пусть ![]() и
и ![]() . Последние углы равны, поскольку они являются вписанными и опираются на одну дугу:
. Последние углы равны, поскольку они являются вписанными и опираются на одну дугу:
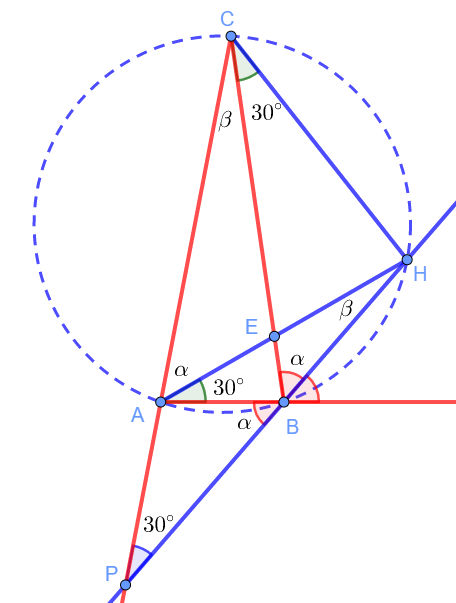
Тогда ![]() . Но также
. Но также ![]() , так как они вписанные и опираются на одну дугу. Но
, так как они вписанные и опираются на одну дугу. Но ![]() по теореме в внешнем угле треугольника. То есть получаем, что
по теореме в внешнем угле треугольника. То есть получаем, что ![]() . Итак,
. Итак, ![]() . Значит, треугольник ACH равнобедренный, и
. Значит, треугольник ACH равнобедренный, и ![]() .
.
Пусть теперь ![]() . Тогда по теореме косинусов для треугольника AHB получаем, что
. Тогда по теореме косинусов для треугольника AHB получаем, что ![]() . Одновременно по теореме косинусов для треугольника BCH получаем, что
. Одновременно по теореме косинусов для треугольника BCH получаем, что ![]() . Используя эти равенства, находим, что
. Используя эти равенства, находим, что ![]() .
.
Наконец, используя подобие треугольников ABP и BCH, находим, что ![]() .
.
Ответ: 9.
| Пример 2. В прямоугольном треугольнике ABC на гипотенузу AB=11 опустили высоту CD=4, которая разделила треугольник на два меньших треугольника, в каждый из которых вписали окружность. Прямая, проходящая через центры этих окружностей, пересекает катеты AC и BC в точках M и N соответственно. Найдите площадь треугольника CMN. |
Сделаем чертёж к заданию с некоторыми дополнительными построениями:
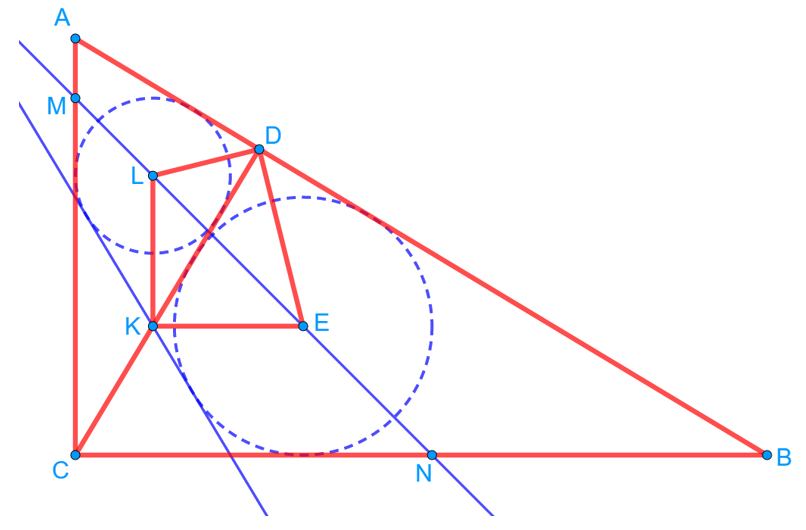
Провели общую внешнюю касательную к окружностям, которая пересеклась с высотой CD в точке K. Поскольку центр вписанной в угол окружности лежит на биссектрисе угла, то ∠ADL = ∠LDK = ∠KDE = ∠EDB = 45°. То есть ∠LDE = 90°. Кроме того, ∠LKE = 90°, так как это угол между биссектрисами смежных углов. Значит, вокруг четырёхугольника LDEK можно описать окружность, поэтому ∠KLE = ∠KDE = 45°, так они являются вписанными и опираются на одну дугу. Ну а поскольку ∠LKE = 90°, то и ∠KEL = 45°.
Докажем теперь, что треугольник LDE подобен треугольнику ABC:
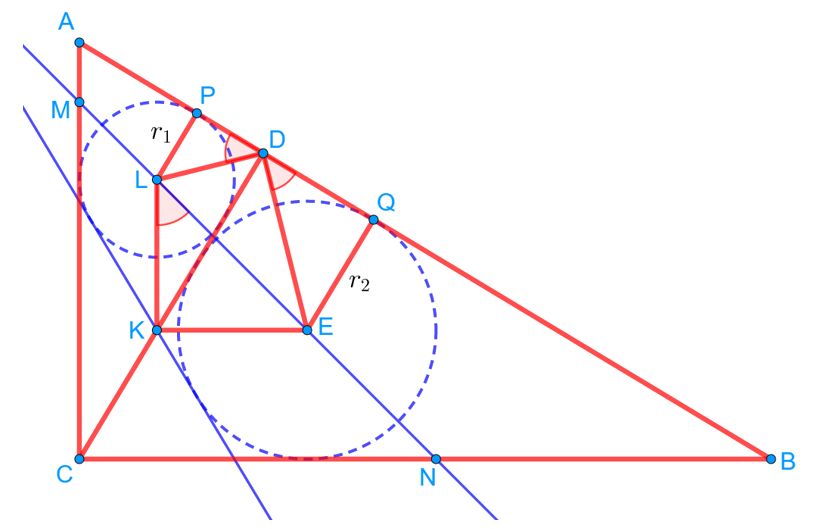
Заметим сперва, что подобны треугольники ADC и CDB, причём коэффициент их подобия равен ![]() , где
, где ![]() и
и ![]() — радиусы вписанных окружностей. Вторая часть равенства получилась из подобия прямоугольных треугольников LDP и EDQ. То есть треугольники LDE и ABC подобны по прямому углу и двум пропорциональным сторонам, образующим этот угол. Значит, ∠ABC = ∠DEL. Поскольку четырёхугольник KLDE вписан в окружность, и треугольники ADC и CDB подобны, верно также, что ∠ABC = ∠ACD = ∠LKD. Значит, прямые AC и LK параллельны, и ∠CMN = ∠KLE = 45°.
— радиусы вписанных окружностей. Вторая часть равенства получилась из подобия прямоугольных треугольников LDP и EDQ. То есть треугольники LDE и ABC подобны по прямому углу и двум пропорциональным сторонам, образующим этот угол. Значит, ∠ABC = ∠DEL. Поскольку четырёхугольник KLDE вписан в окружность, и треугольники ADC и CDB подобны, верно также, что ∠ABC = ∠ACD = ∠LKD. Значит, прямые AC и LK параллельны, и ∠CMN = ∠KLE = 45°.
Значит, прямоугольный треугольник CMN является равнобедренным. Тогда треугольники CED и CEN равны по стороне и двум прилежащим к ней углам, и ![]() . Значит, искомая площадь треугольника CMN равна 8.
. Значит, искомая площадь треугольника CMN равна 8.
Ответ: 8.
| Пример 3. Натуральное число назовём пятнистым, если оно состоит из различных ненулевых цифр, сумма которых делится на 5. Найдите трёхзначный простой делитель суммы всех семизначных пятнистых чисел. |
Для любого набора цифр с суммой, делящейся на 5, в составе семизначных чисел из-за всевозможных перестановок этих цифр местами каждая цифра будет находиться в любом разряде одинаковое число раз. Значит, при вычислении поразрядно суммы всех пятнистых чисел сумма цифр в каждом разряде будет одной и той же. Обозначим эту сумму буквой S. Тогда сумма всех пятнистых чисел равна:
![]()
![]()
У числа 1111111 есть один простой трёхзначный делитель. Это число 239. Получили ответ к заданию. Причём он даже не зависит от условия, что сумма цифр в пятнистых числах делится на 5.
Ответ: 239.
Подготовка к олимпиаде «Высшая проба»
Если у вас есть другие задачи из олимпиады «Высшая проба», которые вы бы хотели решить, пишите условия этих задач в комментариях. Будем их решить и добавлять решения в статью.
Если вам требуются уроки для подготовки к олимпиадам по математике, в том числе к олимпиаде «Высшая проба», обращайтесь ко мне. Я репетитор и специализируюсь на подготовке такого рода. Мои контакты вы найдёте на этой странице. Успехов!
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич
