 Есть такая книга, которая называется “Магия чисел”. Название очень точное и емкое — с помощью чисел можно творить самые настоящие «чудеса». В чем-то это похоже на магию. Эта книга дает очень обширную информацию по теме математических расчетов, подробно рассказывая какими способами их можно упростить.
Есть такая книга, которая называется “Магия чисел”. Название очень точное и емкое — с помощью чисел можно творить самые настоящие «чудеса». В чем-то это похоже на магию. Эта книга дает очень обширную информацию по теме математических расчетов, подробно рассказывая какими способами их можно упростить.
В данной статье приведены 8 наиболее интересных математических трюков и фокусов, которые, несомненно, многим пригодятся в жизни. Ведь вполне может оказаться так, что вам потребуется произвести быстрый расчет, а калькулятора под рукой не окажется. Да и просто периодически производить математический расчет в уме, хотя бы частично — это очень хорошая тренировка для мозга.
Математические трюки, которым не научат в школе
1. Умножение на однозначное число
Произвести умножение на однозначное число в уме — дело довольно простое. Всего-то и нужно, что разбить большое число на несколько «круглых» чисел в соответствии с разрядами (единицы, сотни, тысячи, десятки тысяч и т. д.), умножить полученные числа на данное однозначное число и сложить результаты. Давайте попробуем. Предположим, что требуется умножить 324 на 7.
- 324 мы представим в виде
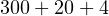 . Такие числа умножать намного легче.
. Такие числа умножать намного легче. - Перемножаем полученные числа на 7 по отдельности:
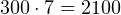 ,
, 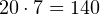 ,
, 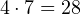 .
. - Осталось только сложить результаты, и мы получаем искомое число 2268.
Разоблачение. Любое число в десятичной системе счисления может быть представлено в стандартном виде:
![]()
![]()
Следовательно, умножение данного числа на однозначное число ![]() равносильно следующей операции:
равносильно следующей операции:
![]()
![]()
![]()
что соответствует представленному выше алгоритму.
2. Квадрат двухзначного числа
Разберём алгоритм действий на конкретном примере. Пусть требуется возвести в квадрат число 43.
- Из числа 43 вычитаем 3, получаем число 40 (делаем его «круглым»). К числу 43 прибавляем то же число 3, получаем число 46.
- Перемножаем полученные числа. Умножить на «круглое» число в уме значительно проще:
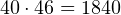 .
. - Возводим в квадрат 3 (число, которое прибавили и вычли в п. 1):
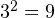 .
. - И прибавляем этот результат к числу, полученному в п. 2 алгоритма:
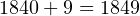 .
.
Вся суть математического трюка в том, чтобы получить два числа, удобные для умножения, лучше всего, когда одно из двухзначных чисел будет «круглым».
Разоблачение. Двузначение число ![]() можно записать следующим образом:
можно записать следующим образом: ![]() . Тогда имеет место равенство:
. Тогда имеет место равенство:
![]()
В соответствии с введёнными обозначениями, в п. 1 алгоритма нами были получены числа: ![]() и
и ![]() . А в п. 3 к произведению этих чисел прибавлялось
. А в п. 3 к произведению этих чисел прибавлялось ![]() . То есть имеет место равенство:
. То есть имеет место равенство:
![]()
3. Квадрат двухзначного числа, оканчивающегося на пятёрку
Гораздо проще возвести в квадрат двухзначное число, на конце которого стоит цифра 5. Ту цифру, что спереди умножаем на число, большее ее на единицу и добавляем в конец 25. Например, чтобы возвести в квадрат число 75, умножаем ![]() , дописываем в конец 25, и получаем 5625.
, дописываем в конец 25, и получаем 5625.
Разоблачение. Двухзначное число с пятёркой на конце можно записать в виде: ![]() . Тогда его квадрат равен:
. Тогда его квадрат равен:
![]()
![]()
То есть возведение двухзначного числа, оканчивающегося на пятёрку, в квадрат равносильно умножению первой цифры этого числа на следующее по порядку число, затем умножению результата на 100 и прибавлению 25, что полностью соответствует описанному выше правилу.
4. Как разделить на однозначное число
Это один из самых нужных нам навыков, на самом деле. С такими расчетами мы сталкиваемся довольно часто. Допустим, нужно разделить число 4512 на 8. Действовать нужно по следующему алгоритму:
- Число, которое мы делим, четырёхзначное. Поэтому сперва нужно найти такое «круглое» число, меньшее на 1 разряд по сравнению с делимым (т. е. трёхзначное), которое при умножении на 8 даёт самый близкий результат к исходному числу, но не превышает его:
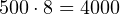 ,
, 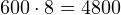 . То есть мы должны получить в итоге 500 с небольшим.
. То есть мы должны получить в итоге 500 с небольшим. - От 4512 отнимем 4000, получаем 512.
- Повторяем действия из п. 1 для числа 512:
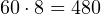 ,
, 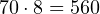 . Нужное нам число равняется 60.
. Нужное нам число равняется 60. - От 512 отнимем 480, получаем 32.
- Делим 32 на 8, получаем 4.
- Складываем 500, 60 и 4, получаем в ответе 564.
Разоблачение. На самом деле, это лишь применение хорошо известного метода деления чисел столбиком к частному случаю деления на однозначное число.
5. Как получить пятнадцать процентов от числа
Для такой операции требуется выполнить следующие действия: от исходного числа вычисляем десять процентов (всего-то и нужно, что перенести запятую на одну цифру влево), полученное разделить на 2 и сложить получившиеся числа. Например, ищем 15% от числа 650.
- 10% от 650 — это 65;
- 65 поделим на два — получим 32,5;
- 65 + 32,5 = 97,5.
Разоблачение. 10% от числа — это его десятая часть, а 5% — это половина от десятой части. Поэтому для того, чтобы найти 15% от числа нужно найти десятую часть от этого числа, затем — половину от десятой части, сложить полученные числа, это и будет являться ответом.
6. Простой математический трюк
Практически все вы сталкивались с таким нехитрым фокусом: загадайте число, умножьте его на 2, прибавьте 12, разделите полученное число на 2, вычтите задуманное число. И всегда загадавший эту загадку верно угадывает ответ. Получилось 6, не так ли? Весь в фокус в том, что шестерку вы получите всегда, какое бы число не было вами загадано.
Почему так происходит? Давайте разберемся.
Разоблачение.
- Пусть исходное число
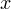 ;
; - Когда вы умножаете на два, вы тем самым удваиваете свое исходное число
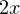 ;
; - Затем идет
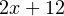 ;
; 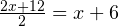 ;
;- И, наконец,
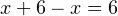 .
.
Это все элементарные алгебраические расчеты, благодаря которым можно прослыть изрядным знатоком математики.
7. Волшебное число 1089
Старинный математический фокус. Необходимо написать трехзначное число, каждая цифра которого будет меньше предыдущей. Например, 974 или 765. Перепишите число наоборот и отнимите от исходного числа. К результату добавьте перевернутый результат и у вас неизменно будет выходить 1089.
Разоблачение. Пусть исходное число ![]() . Поскольку цифры в первом числе расположены в порядке убывания, то при вычитании из него «обратного» числа
. Поскольку цифры в первом числе расположены в порядке убывания, то при вычитании из него «обратного» числа ![]() , придётся занять из разряда десятков и сотен. То есть в результате число единиц будет равно
, придётся занять из разряда десятков и сотен. То есть в результате число единиц будет равно ![]() , число десятков будет равно
, число десятков будет равно ![]() , число сотен будет равно
, число сотен будет равно ![]() . Тогда результатом сложения полученного числа с «обратным» станет число, в котором число единиц равно
. Тогда результатом сложения полученного числа с «обратным» станет число, в котором число единиц равно ![]() , число десятков будет равно
, число десятков будет равно ![]() (то есть 8, а 1 переносим в разряд сотен), число сотен будет равно
(то есть 8, а 1 переносим в разряд сотен), число сотен будет равно ![]()
![]() . Итак, получившееся число равно 1089.
. Итак, получившееся число равно 1089.
8. Правило семидесяти
Данное правило нужно для того, чтобы рассчитать какое количество лет пройдет, пока оставленный вами вклад в банке возрастёт вдвое. Все что нужно — разделить семьдесят на процент годовой ставки. Например, если годовая ставка составляет 5 процентов, то 70 нужно разделить на 5, что равно 14 годам.
Разоблачение. Пусть вы оставили в банке ![]() руб. Процентная ставка по вкладу составляет
руб. Процентная ставка по вкладу составляет ![]() процентов годовых. Тогда через 1 год вклад возрастёт до
процентов годовых. Тогда через 1 год вклад возрастёт до ![]() руб, через 2 года вклад возрастёт до
руб, через 2 года вклад возрастёт до ![]() , через
, через ![]() лет вклад возрастёт до
лет вклад возрастёт до ![]() . Требуется найти через сколько лет вклад удвоится, то есть
. Требуется найти через сколько лет вклад удвоится, то есть ![]() . Откуда получаем:
. Откуда получаем:
![]()
Последнее приближение можно получить строго, используя разложение в ряд. Правда это приближение справедливо только при малых значениях ![]() по сравнению с 1. К примеру, уже для процентной ставки 20% годовых погрешность вычислений составляет порядка полугода.
по сравнению с 1. К примеру, уже для процентной ставки 20% годовых погрешность вычислений составляет порядка полугода.
Вот вы и узнали про математические трюки, которым не научат в школе. Как видите, это действительно, на первый взгляд, отдает волшебством. Но на самом деле, все это лишь холодная математическая логика, которая способна облегчить вам жизнь и помочь выделиться среди круга своих знакомых. А заодно привнести в их жизнь чуточку настоящей магии, полученной в данном случае не за счет ловкости рук, а благодаря знаниям и гибкости ума.
Материал подготовлен репетитором по математике в Москве, Сергеем Валерьевичем
