Поступление в 9 класс лицея ВШЭ – мечта целеустремлённых молодых людей. Это перспективное учебное заведение, обучение в котором станет определяющим этапом в будущей успешной жизни.
Школа мечты
Лицей НИУ ВШЭ сформировался на базе Национального исследовательского университета «Высшая Школа Экономики», основанного в 1992 году. Это лучшая школа города Москвы согласно рейтингу 2016/17 учебного года (1 место) и 5-я в общероссийском списке. Также она занимает:
- 1-е место среди школ социально-экономического;
- 2-е – среди школ социально-гуманитарного;
- 4-е – среди школ филологического направлений.
Для учеников этого учреждения 100 баллов на ЕГЭ – это не миф, и 24 выпускника 2017 года это доказали. Лицей – лидер этого же года среди школ Москвы по количеству победителей в заключительном этапе всероссийской олимпиады школьников.
Учитель – это призвание
Преподаватели учебного заведения не просто читают лекции и проводят практические занятия, они пробуждают интерес, прививают любовь к своим дисциплинам. Занятия проходят в обстановке «на равных», где лекторы преподносят знания так, что их невозможно забыть. Об этом говорят сами ученики. Более 150 учителей – это преподаватели НИУ ВШЭ, имеющие учёные степени, ведущие активную научную деятельность.
Ребёнок сам выбирает уроки!
Лицей работает по университетской системе обучения. В программе реализовано 8 направлений подготовки, занятия проходят по парам, а каждый четверг классы отправляются на учёбу по факультетам. Лицеисты в праве самостоятельно выбирать предметы из числа вариативных, таким образом составляя индивидуальный учебный план.
Обучение в лицее НИУ ВШЭ престижно и подходит для по-настоящему заинтересованной в своём развитии молодёжи. Ученики посещают студенческие факультативы, участвуют в общественных движениях, демонстрируют активную жизненную позицию.
Поступление в 9 класс лицея НИУ ВШЭ: особенности
Зачисление в учебное заведение производится по итогам выполнения комплексных тестов на конкурсной основе. Перевестись в лицей из другой школы нельзя.
3 этапа на пути к поступлению в лицей НИУ ВШЭ
Ниже, как и во всей статье, представлена информация на 2018 год. В последующие годы что-то может поменяться, но в текущем 2018 году поступление можно условно разбить на 3 этапа.
На 1-м этапе абитуриенту предлагают заполнить заявку с необходимой личной информацией и написать эссе, в котором рассказать о себе, достижениях, целях, интересах и опыте, а также причинах желания учиться в лицее. Рассказ не оценивается.
2-й этап в поступлении в лицей – определяющий. Абитуриенты пишут комплексный тест, включающий в себя задания по математике, русскому и иностранному языку. По первым двум дисциплинам в тесте даётся 20 заданий и 1 на знание выбранного иностранного языка в виде рассказала на заданную тему.
Приёмная комиссия рекомендует ориентироваться не на минимальный проходной балл, а на максимум, ведь чем выше будет результат, тем больше шансов на поступление в 9 класс лицея НИУ ВШЭ. Наибольшее количество баллов за тест – 30, проходной минимум – 15. Претенденты на обучение, не набравшие 15 баллов, не будут иметь права на зачисление.
Заключительный 3-й этап – это собрание, на котором претенденты на обучение и их родители ознакомятся с правилами школы и напишут заявления о приёме.
Сроки и порядок испытаний
Приём заявок на поступление в лицей производится в электронной форме на сайте учебного заведения. Для подачи заявления нужно пройти простую регистрацию и получить доступ к личному кабинету. 1 этап продлится до 12 апреля.
Комплексный тест будет проводиться 13 и 20 мая. Продолжительность испытания составит 120 минут. Руководство лицея также отводит 1 резервный день – 27 мая, для абитуриентов, по веской причине не способных пройти тест в заявленные дни. Результаты теста и списки набравших достаточное количество баллов будут объявлены не позднее 10 июня.
Какие знания проверяют при поступлении
Чтобы выдержать вступительные испытания, требуются исключительные знания основной школьной программы 8 класса. Как показывает практика, если с заданиями по гуманитарным дисциплинам справляется большинство школьников, то в области математики от абитуриента требуется не только безупречное знание материала, но и умение применять его для решения довольно сложных заданий, особенно из второй части комплексного теста. В среднестатистических школах этот аспект не охватывается в той степени, в какой он необходим уже на этапе вступительных тестов.
Как упростить поступление в 9 класс лицея ВШЭ
Чтобы облегчить подготовку ребёнка к вступительному тесту, обратитесь за помощью к квалифицированному репетитору. Меня зовут Сергей Валерьевич. Я штатный преподаватель на факультете физики и информационных технологий Московского Педагогического Государственного Университета. Репетитор по математике и физике с непрерывным 10-летним опытом работы (с 2008 года).
Я разработал собственную методику преподавания этих дисциплин, на основе которой успешно обучаю школьников 5-11 классов. Благодаря ей мои ученики достигают поставленных целей: качественно улучшают свои знания по предмету, успешно сдают переводные, выпускные и вступительные экзамены, в том числе в лицей НИУ ВШЭ, а также ЕГЭ и ОГЭ по математике и физике. Я учитываю индивидуальные особенности каждого ребёнка: его уровень мотивации, возможности памяти, скорость восприятия и усвоения материала, исходные знания. По итогам вводного занятия составляю программу, которой следую на протяжение всего периода подготовки.
Как проходят занятия
Заниматься у меня возможно 3-мя способами.
- Индивидуально лично. В этом случае мы встречаемся с учеником с определённым интервалом (оптимально 2 раза в неделю), прорабатываем все пробелы, обучаемся всем приёмам, необходимым на вступительном экзамене.
- Индивидуально онлайн. Как показывает практика, это очень эффективный способ. Идеально подходит в случае невозможности обучаться при личных встречах.
- Подготовка группы из 2-х человек. Бюджетный способ подготовки. Подходит для детей, желающих поступить в лицей вместе.
Успех поступления в 9 класс лицея ВШЭ зависит от серьёзного подхода родителей и ребёнка к подготовке к вступительному тесту. Чтобы обезопасить себя от неудовлетворительных баллов, начните занятия как можно скорее. Позвоните мне (контакты есть на этой странице) и запишитесь на вводное занятие.
Ну и чтобы не быть голословным, предлагаю вам ознакомиться с разбором демонстрационного варианта вступительного экзамена в 9 класс лицея НИУ ВШЭ. Сам вариант доступен для скачивания на сайте лицея. Здесь я привожу свои авторские решения каждого задания в надежде, что кому-то это сможет помочь при подготовке к поступлению в 9 класс лицея ВШЭ.
Разбор вступительного экзамена в 9 класс лицея ВШЭ
| Задание 1. Вычислите
|
Выполним сперва действие в скобках:
![]()
Теперь осталось выполнить деление:
![]()
Итак, ответ: -0,2.
| Задание 2. В коробке лежат 12 белых шаров и 8 черных. Какое минимальное количество шаров, не глядя, надо вытащить из коробки, чтобы среди них точно были 2 белых и 1 черный? |
Заметим сразу, что 13-ти шаров будет достаточно, поскольку максимум среди них может оказаться 12 белых шаров, значит 1 оставшийся будет чёрным. Это удовлетворяет условию задачи. А вот 12-ти уже будет не достаточно, так как все они могут оказаться белыми. Итак, если мы хотим быть уверены, то вытащить нужно минимум 13 шаров.
Ответ: 13.
| Задание 3. Телевизор стоил 10000 рублей. Сначала его цену подняли на 10%, а потом снизили на 10%. Сколько стал стоить телевизор после снижения цены? |
После повышения цены на 10% с 10000 рублей телевизор стал стоить 10000 x 1.1 = 11000 руб. После снижения этой цены на 10% телевизор стал стоить 11000 x 0.9 = 9900 руб.
Ответ: 9900 руб.
| Задание 4. Найдите значение выражения
|
Приведём дроби к общему знаменателю и выполним вычитание по обычным правилам:
![Rendered by QuickLaTeX.com \[ \frac{3\sqrt{2}+4-3\sqrt{2}+4}{(3\sqrt{2}-4)(3\sqrt{2}+4)}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-94542daf462e6342aa99729e54b593eb_l3.png)
Для упрощения знаменателя воспользуемся формулой «разность квадратов», а в числителе просто приведём подобные слагаемые:
![]()
Ответ: 4.
| Занятие 5. Упростите выражение
|
Упростим сперва выражение, находящееся в скобках. Для этого разложим оба знаменателя на множители и приведём дроби к общему знаменателю:
![Rendered by QuickLaTeX.com \[ \frac{x+3}{x(x-3)}+\frac{x-3}{x(x+3)} = \frac{(x+3)^2+(x-3)^2}{x(x-3)(x+3)} = \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4178b15d4ac2b24e7aa5d21b409e026d_l3.png)
![Rendered by QuickLaTeX.com \[ =\frac{x^2+6x+9+x^2-6x+9}{x(x-3)(x+3)} = \frac{2(x^2+9)}{x^3-9x}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c256771960e810a4874c1413461fde10_l3.png)
Теперь настало время умножения:
![]()
Ответ: -2.
Примечание. Понятно, что результат справедлив только для тех ![]() , при которых в ноль не обращается ни один из знаменателей в исходном выражении, то есть для
, при которых в ноль не обращается ни один из знаменателей в исходном выражении, то есть для ![]() .
.
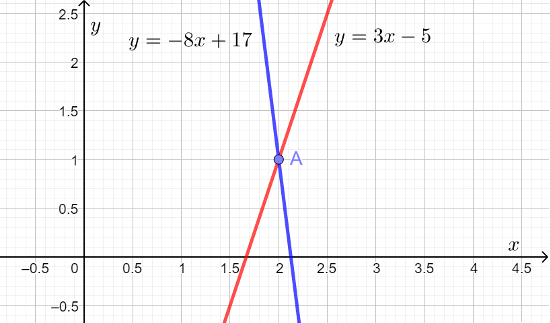
| Задание 6. Найдите ординату точки пересечения прямых: |
В точке пересечения эти прямые имеют одинаковые значения ![]() и
и ![]() . Поэтому имеет место равенство:
. Поэтому имеет место равенство:
![]()
Подставляет это значение в уравнение первой прямой. В результате получаем, что ордината точки пересечения равна:
![]()
Для наглядности изобразим эти прямые на графике. Хотя делать это не обязательно, так как в задании этого и не требуется, иногда действовать таким образом бывает полезно в целях самопроверки. На графике ситуация выглядит следующим образом:
Ответ: 1.
| Задание 7. Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите высоту, проведённую к гипотенузе. |

Находим по теореме Пифагора длину гипотенузы AC:
![]()
То есть гипотенуза равна 10 см. Тогда с одной стороны площадь треугольника ABC равна половине произведения катетов (½·AB·BC = ½·8·6 = 24), то есть 24 квадратных сантиметра, а с другой стороны — это половина произведения искомой высоты BH (обозначим её для удобства буквой ![]() ) на гипотенузу AC:
) на гипотенузу AC:
![]()
Итак, искомая высота равна 4.8 см. Это ответ к заданию.
| Задание 8. Один из корней уравнения |
Если число 8 является корнем этого уравнения, то при подстановке этого числа вместо ![]() в это уравнение должно получиться верное равенство. То есть имеет место равенство:
в это уравнение должно получиться верное равенство. То есть имеет место равенство:
![]()
Из этого равенства получаем, что ![]() .
.
| Задание 9. Произведение двух последовательных натуральных чисел больше их суммы на 109. Найдите большее из этих чисел. |
Пусть первое число равно ![]() , тогда следующее за ним натуральное число равно
, тогда следующее за ним натуральное число равно ![]() . По условию произведение этих чисел на 109 больше их суммы. То есть имеет место уравнение:
. По условию произведение этих чисел на 109 больше их суммы. То есть имеет место уравнение:
![]()
Преобразуем это уравнение. В результате приходим к следующему уравнению:
![]()
Находим корни этого уравнения по теореме Виета (сумма корней равна 1, а их произведение равно -110). Первый корень равен -10, то есть отрицателен (не является натуральным), поэтому не подходит. А второй корень равен 11. Следующее за ним натуральное число — это число 12.
Итак, ответ: 12.
| Задание 10. Диагонали ромба численно равны корням уравнения |
Корни этого уравнения считать не обязательно. Это неудобно, поскольку придётся работать с иррациональными выражениями, и повышается риск возникновения ошибки при вычислениях. Существует гораздо более изящное решение этой задачи, с которым ученики могут ознакомиться на уроках с профессиональным репетитором по математике. Суть его в следующем.
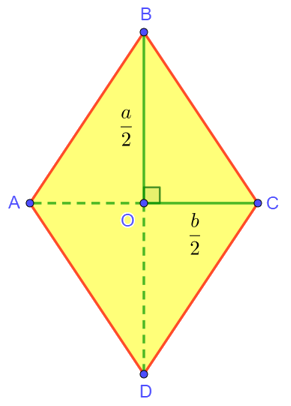
Как видно из рисунка, квадрат стороны ромба равен сумме квадратов половин диагоналей этого ромба:
Действительно, диагонали ромба, как известно, пересекаются под прямым углом и точкой пересечения делятся пополам. То есть если обозначить диагонали ромба буквами ![]() и
и ![]() (они же по условию буду численно равны корням квадратного уравнения), то в соответствии с теоремой Пифагора для треугольника BOC на рисунке будет иметь место равенство:
(они же по условию буду численно равны корням квадратного уравнения), то в соответствии с теоремой Пифагора для треугольника BOC на рисунке будет иметь место равенство:
![Rendered by QuickLaTeX.com \[ BC^2 = \left(\frac{a}{2}\right)^2+\left(\frac{b}{2}\right)^2 = \frac{a^2+b^2}{4}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c468ead2a72d8ddd2d3019373382ec88_l3.png)
Продолжим преобразовывать полученное выражение и сделаем, на первый взгляд, странное, но, как далее окажется, очень полезное преобразование: добавим и вычтем в числителе выражение ![]() :
:
![]()
Зачем мы это сделали? Дело в том, что теперь в числителе можно воспользоваться формулой «квадрат суммы», чтобы представить его в более удобном для решения задачи виде:
(1) ![]()
Почему эта форма для нас удобнее? Потому что мы имеем дело с приведённым квадратным уравнением ![]() , для которого мы можем применить теорему Виета и получить следующий результат:
, для которого мы можем применить теорему Виета и получить следующий результат:
![Rendered by QuickLaTeX.com \[ \begin{cases} a+b=\sqrt{40} \\ ab=2. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f1dc5238bf2dfebedb8d833f44ddd11b_l3.png)
После подстановки этих выражений в полученную формулу (1) мы мгновенно избавляемся от всех квадратных корней и получаем искомый ответ:
![Rendered by QuickLaTeX.com \[ BC^2 = \frac{(a+b)^2-2ab}{4} = \frac{\left(\sqrt{40}\right)^2-2\cdot 2}{4} = 9. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7f419d5c5e898e2f9994f99c581084a7_l3.png)
Итак, сторона ромба равна ![]() .
.
Так что не всегда нужно решать задачу «в лоб». Иногда есть более изящные способы, которые позволят вам упростить вычисления и избежать ошибок. Именно для того, чтобы научиться таким способам, которым вас не научат в обычной школе, и требуются занятия с профессиональным репетитором по математике.
Если вам требуется подготовка к поступлению в 9 класс лицея ВШЭ, обращайтесь к репетитору по математике и физике в Москве с большим опытом Сергею Валерьевичу. Контакты преподавателя вы найдёте на этой странице. Также вы можете воспользоваться сайтом cleverfox.info, на котором размещено множество тренировочных вариантов вступительных тестов в лицей ВШЭ с ответами и подробными решениями для самопроверки. Всего доброго и успехов в подготовке!



![Rendered by QuickLaTeX.com \[ \left(\frac{x+3}{x^2-3x}+\frac{x-3}{x^2+3x}\right)\cdot\frac{9x-x^3}{x^2+9}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e18a2ef73a129b27e2753c3be32873f4_l3.png)