Поступление в школу 57 г. Москвы – мечта многих талантливых школьников. Но эта престижная школа предъявляет соискателями серьезные требования. К сожалению, не все учащиеся получают требуемый для поступления уровень подготовки в обычной школе. Чтобы избежать ненужного разочарования, воспользуйтесь услугами репетитора по математике. Именно занятия с профессиональным репетитором помогут вашему ребенку достичь поставленной цели!

История школы №57 г. Москвы берёт своё начало в 1968 году, когда был набран первый математический класс. В то время занятия для учеников проводил известный математик и педагог Н. Н. Константинов, методика преподавания которого используется в школе и по сей день. В настоящее время школа №57 г. Москвы заработала репутацию серьёзного учебного заведения. Её ученики регулярно становятся призёрами различных олимпиад и городских конкурсов, блестяще сдают выпускные экзамены и поступают в самые престижные отечественные и зарубежные вузы. Не удивительно, что учащиеся многих других школ мечтают о поступлении в школу 57 г. Москвы!
Особенности поступления в школу 57 г. Москвы
В школу 57 ведётся набор в различные спецклассы, направления подготовки в которых варьируются от гуманитарного, биомедицинского и биологического до математического, математико-информационного, математико-экономического и физико-математического.
С подробной информацией о поступлении в школу 57 г. Москвы вы можете ознакомиться на сайте образовательного учреждения. В данной статье для ознакомления представлена актуальная на 2019 год информация. Вступительные экзамены проходят обычно в марте-апреле. Регистрация на вступительные экзамены открывается обычно в феврале. Общий экзамен по математике для всех спецклассов, за исключением гуманитарного, проводится в единый день. Дальнейшие испытания (устные и письменные) проводятся в соответствии с индивидуальным расписанием для каждого спецкласса.

При этом существует ряд особенностей, о которых родителя стоит знать:
- каждый ученик имеет право поступать в несколько спецклассов одновременно, чтобы в случае успешной сдачи вступительных экзаменов иметь возможность выбора наиболее интересного ему направления обучения;
- при составлении списка рекомендованных к зачислению организаторы вступительных испытаний учитывают не только результаты экзаменов, но и проявленную ребёнком заинтересованность и мотивацию к обучению именно в этой школе;
- поступление в школу 57 — это сложный конкурсный процесс, который невозможно успешно пройти без качественной подготовки, которую, к сожалению, в настоящее время не в состоянии обеспечить обычная средняя общеобразовательная школа.
Поступление в школу 57 с репетитором
Как показывает практика, лучшим вариантов подготовки к поступлению в школу 57 являются индивидуальные занятия с профессиональным репетитором. В процессе этих занятий ваш ребёнок научится свободно отвечать на вопросы преподавателя, а также решать задачи даже самого сложного уровня. Опыт показывает, что серьезная подготовка с репетитором позволяет существенно улучшить результаты, получаемые школьниками на вступительных экзаменах. Это утверждение подтверждают достижения моих учеников, которые успешно преодолели вступительные испытания и ныне являются счастливыми учениками школы №57 города Москвы.
За годы работы я разработал собственную методику, основанную на индивидуальном подходе. Благодаря ей мои ученики успешно сдают вступительные экзамены в лучшие школы г. Москвы, в том числе в школу №57.
Свои занятия я провожу дистанционно (по скайпу с использованием интерактивной онлайн-доски). На первом занятии мы разбираем с учеником несколько специально подобранных заданий. Это помогает определить начальный уровень знаний и способностей ученика, а также выявить его индивидуальные особенности. После этого я составляю индивидуальный план работы, который корректируется и дополняется в дальнейшем в процессе обучения.
Периодичность занятий определяется индивидуально. Продолжительность урока также зависит от конкретной ситуации, но чаще всего она составляет 60-90 мин. Связаться со мной просто. Мои контакты вы можете найти на этой странице.
Поступление в школу 57 во много раз повысит шансы ребёнка стать успешным в будущем. Помните, что успех на 90% зависит от усердия и желания учиться. А моя авторская методика, учитывающая индивидуальные особенности ученика, ускорит достижение желаемого результата и поможет успешно сдать вступительные экзамены!
Ну и напоследок представлю вашему вниманию разбор демонстрационного варианта общего письменного вступительного экзамена по математике. Задания были выложены на сайте школы. Грубо говоря, это самая простая часть, которая ожидает вас на вступительных испытаниях. Но и здесь есть несколько интересных задач, с которыми стоит ознакомиться.
Разбор демоварианта вступительного экзамена по математике в школу 57
|
Задание 1. Вычислите: |
Вычисляем по действиям:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]() .
.
|
Задание 2. Длина отрезка AB составляет 12 см, а |
Поскольку длина отрезка AB равна 12 см, то ![]() его длины составляют
его длины составляют ![]() см. Эта длина составляет
см. Эта длина составляет ![]() длины отрезка CD. Значит, длина отрезка CD равна
длины отрезка CD. Значит, длина отрезка CD равна ![]() см.
см.
|
Задание 3. Решите задачу. В магазин привезли 18 т картофеля. В первый день продали 40% всего картофеля, во второй день 25% остатка. Сколько тонн картофеля осталось продать после двух дней торговли? |
Поскольку всего картофеля было 18 т, а в первый день продали 40% от этого количества, то в тоннах это равно ![]() т. Значит, после первого дня в магазине осталось
т. Значит, после первого дня в магазине осталось ![]() т картофеля. Поскольку во второй день было продано 25% остатка, то в тоннах это составляет
т картофеля. Поскольку во второй день было продано 25% остатка, то в тоннах это составляет ![]() т. Значит, после двух дней магазину осталось продать
т. Значит, после двух дней магазину осталось продать ![]() т картофеля.
т картофеля.
|
Задание 4. Решите уравнение: |
Чтобы избавиться от знаменателей, умножим обе части этого уравнения на 6:
![]()
Далее преобразуем получившееся уравнение:
![]()
![]()
![]()
![]()
|
Задание 5. Разложите на множители |
Используем формулы сокращённого умножения «квадрат суммы» и «разность квадратов»:
![]()
![]()
|
Задание 6. Составьте уравнение прямой, пересекающей оси координат в точках |
Уравнение прямой в общем виде выглядит следующим образом: ![]() . Подставляем координаты точки B в это уравнение:
. Подставляем координаты точки B в это уравнение: ![]() , откуда получаем, что
, откуда получаем, что ![]() . Теперь подставляем координаты точки A в это уравнение:
. Теперь подставляем координаты точки A в это уравнение: ![]() , откуда получаем
, откуда получаем ![]() . Итак, искомое уравнение прямой имеет вид:
. Итак, искомое уравнение прямой имеет вид: ![]() .
.
|
Задание 7. Сейчас Коле 12 лет. Шесть лет назад он был в 6 раз моложе своего учителя математики. Через сколько лет Коля будет в 2 раза младше своего учителя математики? |
Шесть лет назад Коле было ![]() лет. Тогда он был в 6 раз моложе своего учителя математики. Значит, тогда учителю математики было
лет. Тогда он был в 6 раз моложе своего учителя математики. Значит, тогда учителю математики было ![]() лет. То есть сейчас учителю математики
лет. То есть сейчас учителю математики ![]() года. Пусть через
года. Пусть через ![]() лет Коля станет в 2 раза младше своего учителя математики. Тогда имеет место равенство:
лет Коля станет в 2 раза младше своего учителя математики. Тогда имеет место равенство:
![]()
![]()
![]()
![]()
|
Задание 8. Внутри равностороннего треугольника ABC выбрана точка M, а на стороне BC выбрана точка D. При этом |
Изобразим ситуацию на рисунке:
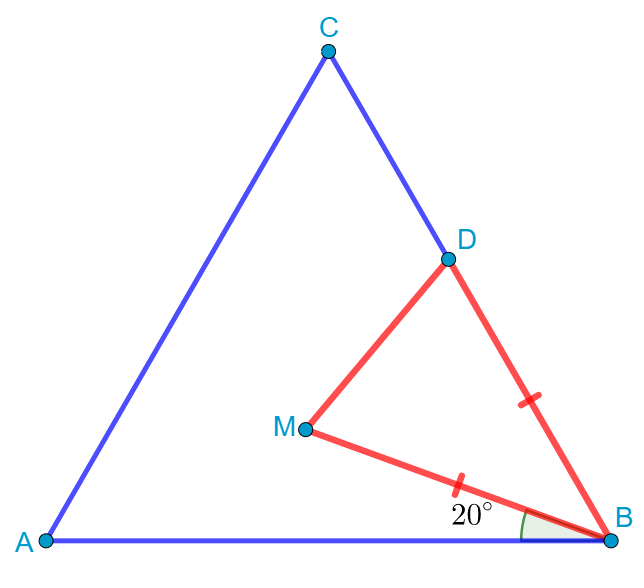
Так как треугольник ABC правильный, то ![]() . Тогда
. Тогда ![]() . Так как треугольник BMD равнобедренный с основанием MD, и сумма внутренних углов любого треугольника равна
. Так как треугольник BMD равнобедренный с основанием MD, и сумма внутренних углов любого треугольника равна ![]() , то
, то
![]()
Тогда ![]() .
.
|
Задание 9. В семье три сына Петя, Вася и Толя. Толя празднует свой день рождения через 40 дней после Васи, а Вася через 40 дней после Пети. В этом году день рождения Пети выпадает на вторник. На какой день недели выпадет день рождения Толи? |
Если Петя празднует свой день рождения во вторник, то Толя празднует свой день рождения через 80 дней, то есть через 11 недель и 3 дня. Значит, день рождения Толи будет через 3 дня после вторника, то есть в пятницу.
|
Задание 10. Среднее арифметическое двух чисел составляет 60% от большего из них. Во сколько раз среднее арифметическое этих чисел больше меньшего числа? |
Пусть меньшее число равно ![]() , а большее число равно
, а большее число равно ![]() . Поскольку их среднее арифметическое составляет 60% от большего из них, то
. Поскольку их среднее арифметическое составляет 60% от большего из них, то ![]() . Из последнего равенства получаем, что
. Из последнего равенства получаем, что ![]() . Значит, среднее арифметическое этих чисел в
. Значит, среднее арифметическое этих чисел в ![]() раза больше меньшего из этих чисел.
раза больше меньшего из этих чисел.
|
Задание 11. Существует ли треугольник АВС, в котором медиана, проведённая из вершины А, перпендикулярна биссектрисе угла В, а медиана, проведённая из вершины В, перпендикулярна биссектрисе угла С? |
Такого треугольника не существует. Докажем это. Предположим обратное. Тогда имеет место ситуация, изображенная на рисунке:
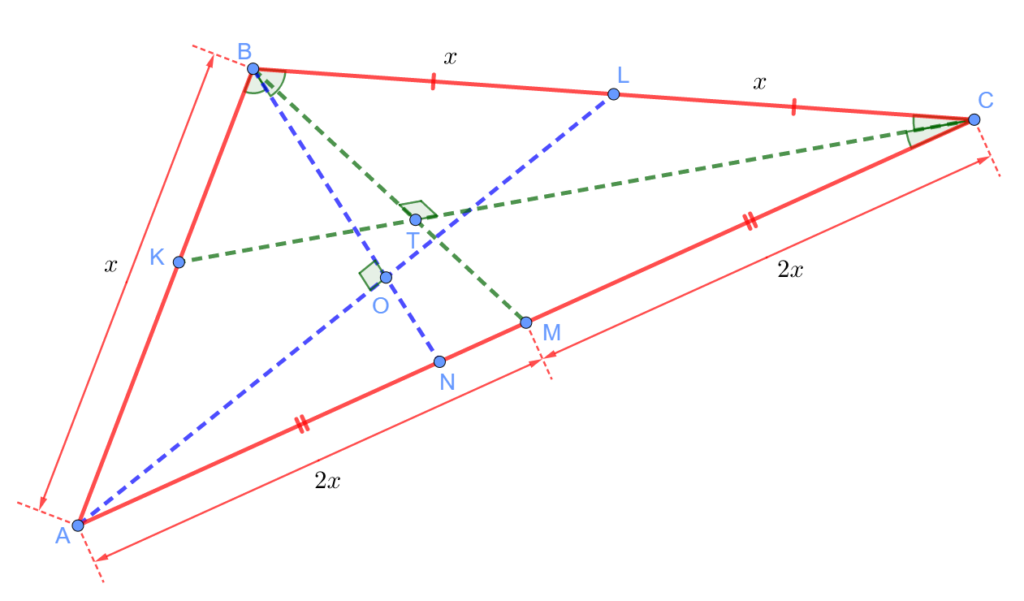
Прямоугольные треугольники ABO и BOL равны по катету и острому углу, поэтому ![]() . Аналогично, прямоугольные треугольники CBT и CTM равны по катету и острому углу, поэтому
. Аналогично, прямоугольные треугольники CBT и CTM равны по катету и острому углу, поэтому ![]() . Но тогда стороны треугольника ABC равны:
. Но тогда стороны треугольника ABC равны: ![]() ,
, ![]() и
и ![]() . Получается, что
. Получается, что ![]() , но это невозможно, так как каждая сторона в треугольнике должна быть меньше суммы двух других сторон (неравенство треугольника). Противоречие.
, но это невозможно, так как каждая сторона в треугольнике должна быть меньше суммы двух других сторон (неравенство треугольника). Противоречие.
|
Задание 12. Разрежьте прямоугольный участок земли на участки одинаковой площади так, чтобы на каждом участке стоял ровно один домик. Все квадратики имеют одинаковую площадь:  |
Ниже приведён правильный вариант разделения на участки:

|
Задание 13. Школьник Петя записал по кругу все цифры от 0 до 9 в некотором порядке. Затем он сложил все пары соседних чисел и выписал десять полученных сумм. Оказалось, что среди этих сумм всего три различных. Приведите пример такого расположения чисел. |
Пример правильного расположения чисел на рисунке снизу:
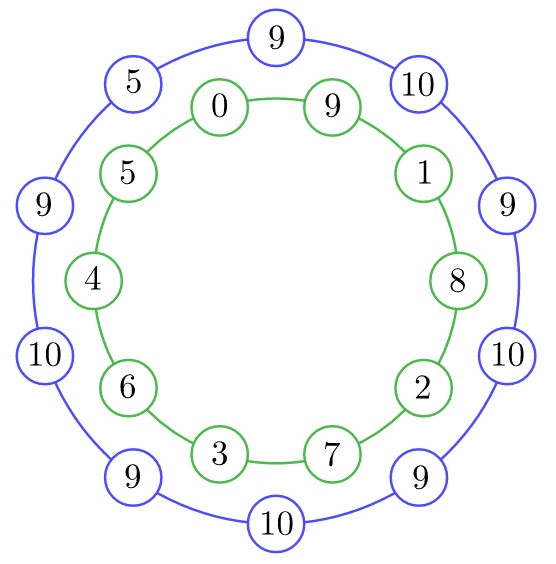
Разбор демонстрационного варианта представлен репетитором по математике и физике Сергеем Валерьевичем
