В данной статье речь пойдёт о поступлении в школу №179 г. Москвы. Это одна из сильнейших школ с точки зрения преподавания математики и физики, что подтверждают высокие позиции школы в различных рейтингах. Учащиеся этой школы регулярно становятся призёрами всевозможных олимпиад, а выпускники практически поголовно становятся студентами ведущих высших учебных заведений страны, о чем свидетельствует статистика, представленная на официальном сайте школы.
Неудивительно, что многие родители желают, чтобы их дети получили образование именно в этом учебном заведении. Ведь качественное образование в школе является залогом успеха во взрослой жизни. Однако именно по этой причине конкурс при поступлении в школу 179 весьма высок. Каждый абитуриент обязан сдать вступительные экзамены, причём довольно сложные. Поэтому перед поступлением всегда возникает вопрос, как эффективно подготовиться к вступительным экзаменам.
Подготовка к поступлению в школу 179 с репетитором
 Ко мне, как к репетитору по математике и физике, часто обращаются родители учеников с просьбой подготовить их ребёнка к вступительным испытаниям в школу 179. За многие годы своей репетиторской практики мне приходилось работать с совершенно разными учениками, в том числе очень способными и мотивированными. Однако всем без исключения требовалась серьёзная подготовка к вступительным испытания. Ни один из них не был достаточно хорошо подготовлен, чтобы поступить в школу 179 без помощи профессионального репетитора. И неважно, были ли они в школе отличникам или нет. А все потому, что обычная школа не даёт необходимого набора знаний, умений и навыков, с помощью которых можно успешно сдать вступительные испытания в школу 179. Причин тому множество. Всё они связаны с насущных проблемами современного школьного образования. Об этом можно долго рассуждать, но факт остаётся фактом. Поступление в школу 179 требует дополнительной подготовки, помимо школьной.
Ко мне, как к репетитору по математике и физике, часто обращаются родители учеников с просьбой подготовить их ребёнка к вступительным испытаниям в школу 179. За многие годы своей репетиторской практики мне приходилось работать с совершенно разными учениками, в том числе очень способными и мотивированными. Однако всем без исключения требовалась серьёзная подготовка к вступительным испытания. Ни один из них не был достаточно хорошо подготовлен, чтобы поступить в школу 179 без помощи профессионального репетитора. И неважно, были ли они в школе отличникам или нет. А все потому, что обычная школа не даёт необходимого набора знаний, умений и навыков, с помощью которых можно успешно сдать вступительные испытания в школу 179. Причин тому множество. Всё они связаны с насущных проблемами современного школьного образования. Об этом можно долго рассуждать, но факт остаётся фактом. Поступление в школу 179 требует дополнительной подготовки, помимо школьной.
Вопрос в том, как эту подготовку получить. Курсов подготовки к вступительным экзаменам при школе нет. Да и если бы они были, толку от них было бы очень мало. Проблема в том, что занятия на курсах мало чем отличаются от школьных. Так что на выходе вы получаете тот же результат, что и при обучении в школьном классе. Кроме того, курсы могут как-то пригодиться скорее для «натаскивания» на однотипные задания. Однако на вступительных экзаменах в школу 179 ежегодно предлагаются различные задачи, и такой способ подготовки заранее обречён на провал.
Так что в действительности существуют лишь три основных способа подготовки к поступлению в школу 179:
- Самостоятельная подготовка. На самом деле это очень хороший способ. И без него не обойдётся ни один другой вариант подготовки. Однако ограничиться только этим способом, как показывает практика, не получится для поступления в школу 179. Проблема в том, что на это может уйти очень много времени. Да и не может школьник в его возрасте организовать для себя обучение так, чтобы оно было эффективным. Он просто не в состоянии подобрать нужные задачи и научиться решать их без помощи наставника, чтобы быть во всеоружии на экзамене, когда попадётся сложная олимпиада задача. В определённой степени могут помочь родители, но и они далеко не всегда являются экспертами в вопросах образования. Да и большая часть знаний по математике, полученных в школьные и студенческие годы, обычно благополучно забывается во взрослой жизни.
- Занятия в математических кружках. Это также довольно хороший вариант подготовки. Но лишь в том случае, если ученик уже мотивирован и увлечён математикой. Проблема в том, что влиться в образовательный процесс в этом случае чрезвычайно сложно. Обычно эти кружки плотно укомплектованы и вновь прибывшему школьнику бывает очень сложно приспособиться к тому темпу, который задаётся на занятиях. В результате преподаватель кружка не особенно заботится о проблемах каждого конкретного учащегося. У него просто не хватает на это времени. Для начинающих школьников, особенно если преподавание математики в его школе ведётся на низком уровне, очень сложно включиться в работу. Очень многие школьники из-за этого уходят из таких кружков, толком так и начав заниматься. И обидно то, что происходит это не из-за отсутствия способностей к математике, которые всегда можно развить, а из-за специфики организации занятий в таких кружках. Кроме того, в математических кружках не готовят целенаправленно к вступительному экзамену в школу 179.
- Поступление в школу 179 с репетитором. Как показывает практика, именно занятия с репетитором являются наиболее эффективным способом подготовки к школе 179. Только от занятий с опытным репетитором, знающим специфику вступительных экзаменов в школу 179, вы получите максимальный эффект, необходимый для успешного поступления и обучения в школе 179. Ведь все внимание преподавателя на занятии сконцентрировано на ученике. Репетитор постоянно следит за успехами и неудачами подопечного и обеспечивает оптимальный для него темп усвоения учебного материала. На своих занятиях опытный репетитор целенаправленно научит вас решать сложные олимпиадные задачи по математике, встречающиеся на вступительном экзамене в школу 179, которые обычно даже не рассматриваются на уроках в школе. При этом нет необходимости выискивать их самостоятельно в бесконечном множестве различных источников, подбирать необходимые именно для вступительного экзамена. Всё это предоставит вам профессиональный репетитор. Он же направит вас в решении, покажет наиболее оптимальные способы решения различных задач, научит приёмам решения математических задач повышенной сложности, так что вы будете во всеоружии на экзамене и без труда справитесь даже с самыми сложными и непонятыми с первого взгляда заданиями. В результате на выходе вас ожидает намного лучший результат за то же время обучения, чем если бы занимались в кружках или самостоятельно.
Но и чтобы не быть голословным, предлагаю разобрать несколько примеров заданий из вступительного экзамена по математике в школу 179. Посмотрим, как их решают школьники с использованием тех знаний, которые они получили в школе, и как они решаются более эффективно с использованием методов, которым обучают своих учеников на занятиях профессиональные репетиторы.
Разбор заданий вступительного экзамена по математике в школу 179
Для примера разберём некоторые задачи из устной части вступительного экзамена в 7 класс школы №179, который проходил в 2016 году. Эти задания были выложены в интернете в свободном доступе. Здесь я цитирую тексты заданий и привожу собственные подробные решения каждого из заданий, чтобы у каждого желающего была возможность самостоятельно в них разобраться.
Попробуйте решить каждую задачу самостоятельно, а затем сравните своё решение с представленным здесь. Это гораздо эффективнее, если вы хотите научиться решать задачи самостоятельно. Кроме того, кто знает, может быть вы сможете найти более красивое и простое решение, чем моё. Если найдёте, пишите его в комментариях.
| Пример 1. Можно ли занумеровать рёбра куба натуральными числами от 1 до 12 так, чтобы для каждой вершины куба сумма номеров рёбер, которые в ней сходятся, была одинакова? |
Чтобы ответить на вопрос данной задачи, нужно сперва вычислить, какой должна быть эта «одинаковая» сумма. Всего вершин у куба ![]() , а сумма всех натуральных чисел от
, а сумма всех натуральных чисел от ![]() до
до ![]() равна
равна ![]() . Предположим, что нам удалось решить задачу, и сумма в каждой вершине оказалась равной
. Предположим, что нам удалось решить задачу, и сумма в каждой вершине оказалась равной ![]() . Тогда сумма во всех
. Тогда сумма во всех ![]() вершинах равна
вершинах равна ![]() . Но эта сумма всех номеров рёбер, посчитанная дважды. Значит,
. Но эта сумма всех номеров рёбер, посчитанная дважды. Значит, ![]() . То есть
. То есть ![]() . Однако такого быть не может, поскольку
. Однако такого быть не может, поскольку ![]() должна выражаться натуральным числом. Получили противоречие. Значит, занумеровать рёбра куба таким образом нельзя.
должна выражаться натуральным числом. Получили противоречие. Значит, занумеровать рёбра куба таким образом нельзя.
Как видите, эта задача относится к особой категории, для решения которых требуется составить конкретный пример, либо доказать, что решения не существует. Излишне добавлять, что такие задачи обычно просто не решают на уроках в обычной школе, ведь для этого от школьника требуются особые навыки, развитие которых выходит за рамки стандартной школьной программы.
Следующая задача тоже на «составление решения». Только на этот раз она сформулирована таким образом, что известно заранее, что решение есть. Требуется «сконструировать» это решение.
| Пример 2. Нарисуйте на клетчатой бумаге треугольник и шестиугольник с вершинами в узлах сетки так, чтобы периметр и площадь треугольника были равны периметру и площади шестиугольника. |
В качестве решения данной задачи подходит следующий пример:
Действительно. В этом случае площади обеих фигур равны по ![]() клетки, а периметры — по
клетки, а периметры — по ![]() сторон клеток и
сторон клеток и ![]() диагонали клеток.
диагонали клеток.
Существуют целые методики применения таких задач в обучении школьников математики, которые я, как репетитор по математике, применяю на своих занятиях с учениками. Это помогает улучшить наглядное мышление школьников, что помогает им в значительной мере в дальнейшем при решении сложных задач по геометрии, а также при поступлении в школу 179. Жаль, что курс математики в обычной школе сильно ограничен по времени, так что на решение подобных задач у школьного учителя не хватает обычно ни времени, ни желания.
| Пример 3. Яблоко и апельсин вместе весят столько же, сколько груша и персик. Яблоко вместе с грушей весят меньше, чем апельсин с персиком, а груша вместе с апельсином весят меньше, чем яблоко с персиком. Какой из фруктов самый тяжёлый? |
Такие формулировки вызывают у многих школьников ступор, причём иногда даже у довольно сообразительных. Особенно это касается стрессовых ситуаций, как, например, на вступительном экзамене. Причём, как только школьник переступает порог кабинета, в котором проходил экзамен, решение приходит само собой. После чего бедному школьнику остаётся только корить себя за то, что он слишком сильно нервничал. А ведь психологическая подготовка перед экзаменом не менее важна, чем предметная. О чём прекрасно знает каждый профессиональный репетитор.
На самом деле эта задача решается довольно просто следующим образом:
1) Известно, что яблоко и апельсин вместе весят столько же, сколько груша и персик, то есть имеет место следующее условное равенство:
Я+А=Г+П.
2) Известно также, что яблоко вместе с грушей весят меньше, чем апельсин с персиком, то есть верно также следующее неравенство:
Я+Г<А+П.
Значит, если поменять местами грушу и апельсин на чашах весов, то перетянет чаша с апельсином. Значит, груша весит меньше апельсина: Г<А. Но тогда, чтобы выполнялось равенство, нужно, чтобы яблоко весило меньше персика: Я<П.
3) Известно также, что груша вместе с апельсином весят меньше, чем яблоко с персиком. То есть имеет место неравенство:
Г+А<Я+П.
Значит, если поменять местами яблоко и грушу на чашах весов, то перетянет чаша с яблоком. То есть яблоко весит больше груши: Г<Я. Но тогда, чтобы выполнялось равенство, нужно, чтобы апельсин весил меньше персика: А<П.
Итак, получилось, что Г<Я, Я<П, Г<А, А<П. Глядя на эти неравенства, получаем, что Я<П, Г<П, А<П. Значит, каждый фрукт весит меньше персика. То есть персик — самый тяжёлый фрукт.
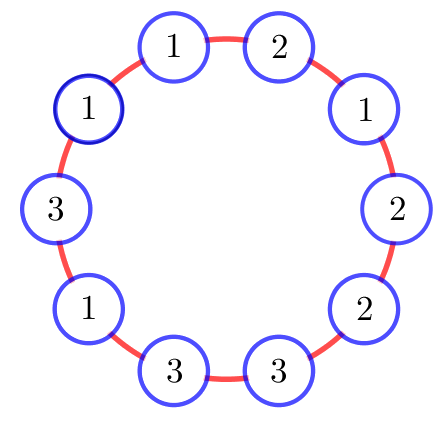
| Пример 4. Расставьте по кругу четыре единицы, три двойки и три тройки так, чтобы сумма любых трех последовательно идущих чисел не делилась на 3. |
Это ещё одна интересная задача на составление примера решения. Подготовленный ученик без труда с ней справится. Правильный вариант расстановки показан на рисунке:
Попробуйте решить похожую задачу, связанную с расстановкой чисел по окружности. Если вам не поддалась предыдущая задача, возможно, вооружившись полученным опытом, у вас получится решить следующую.
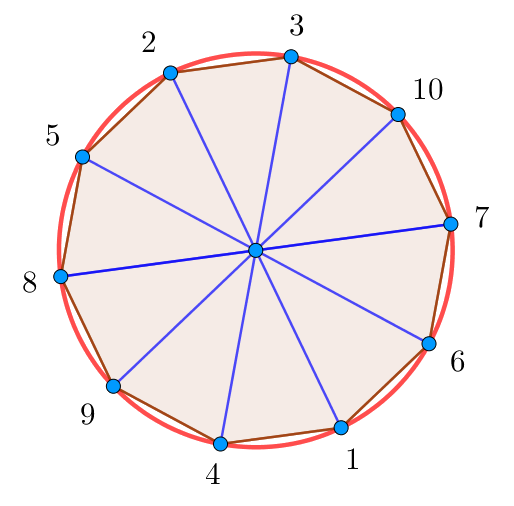
| Пример 5. На окружности поставили 10 точек так, что расстояния между соседними точками одинаковы. Можно ли числа от 1 до 10 расставить рядом с этими точками так, чтобы для любых двух соседних чисел их сумма равнялась сумме двух диаметрально противоположных чисел? |
Да, это возможно. Пример правильной расстановки показан на рисунке:
| Пример 6. Число 111…111 (2016 единиц) разделили на 3. Сколько нулей получилось в записи частного? |
Разделим данное число на группы по три единицы:
111 111 … 111 111
Всего таких групп будет 672. Число 111 делится на 3 с результатом 37. Поэтому после деления исходного числа на 3 получится следующее число:
37 037 037 … 037 (групп 037 в числе будет 671).
В каждой из 671 группы есть по одному нулю. То есть в записи частного будет 671 нуль.
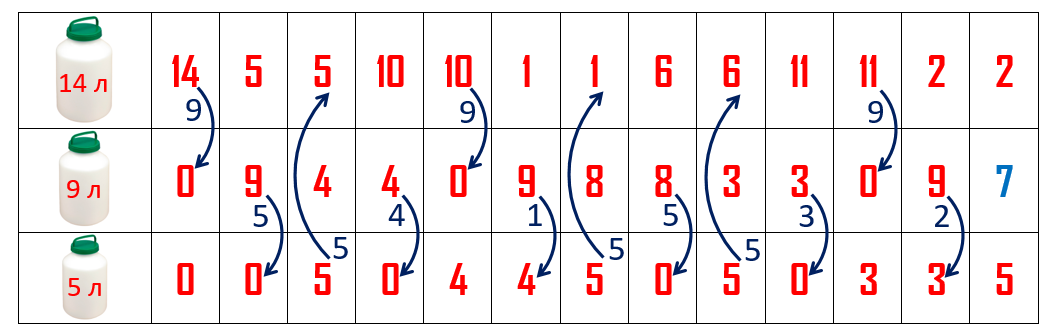
| Пример 7. Имеются 3 бидона ёмкостью 14, 9 и 5 литров. В первом бидоне 14 литров молока, остальные бидоны пустые. Как получить во втором бидоне 7 литров молока, не пользуясь другими сосудами. |
Это едва ли не наиболее часто встречающийся тип задач из вступительных экзаменов в различные школы, лицеи и гимназии. В школе обычно им не уделяют должного внимания, разве что в редких случаях на факультативах. Я, как и многие другие профессиональные репетиторы по математике, предлагаю своим ученикам следующий подход к решению таких задач.
Составим таблицу, состоящую из трёх строк, которые будут соответствовать трём бидонам. Будем переливать молоко из одного в другой, фиксируя каждое переливание в этой таблице. При этом будем стараться переливать молоко не случайным образом, а так, чтобы нигде не возвращаться к исходном состоянию, а получать только новые. И тогда, если задача имеет решение, мы обязательно рано или поздно к нему придём. Получаем следующую последовательность «переливаний»:
Встречаются на вступительном экзамене по математике в школу 179 и задачи, для решения которых требуется обладать нестандартным математическим мышлением и уметь увидеть, а иногда даже угадать подход, который нужно применить для решения. Хорошим примером является следующая задача.
| Пример 8. Злая Королева разложила 100 одинаковых фишек. Каждая фишка покрашена с одной стороны синей краской, а с другой — красной. Ровно 10 фишек лежат красной стороной вверх, остальные — синей. Королева завязала глаза Алисе, размешала фишки на столе, не меняя цветов, и приказала разделить фишки на две части, в каждой из которых будет одинаковое число фишек, лежащих красной стороной вверх. Как Алисе выполнить приказ злой Королевы? |
Алисе нужно взять любые ![]() фишек. Пусть в этой группе из
фишек. Пусть в этой группе из ![]() фишек будет
фишек будет ![]() фишек, лежащих красной стороной вверх, причём
фишек, лежащих красной стороной вверх, причём ![]() может быть одним из чисел
может быть одним из чисел
![]()
Тогда среди оставшихся ![]() фишек будет содержаться
фишек будет содержаться ![]() фишек, лежащих красной стороной вверх. После этого Алиса должна перевернуть все выбранные фишки. Тогда количество фишек в выбранной Алисой кучке, которые окажутся лежащими красной стороной вверх, станет равно
фишек, лежащих красной стороной вверх. После этого Алиса должна перевернуть все выбранные фишки. Тогда количество фишек в выбранной Алисой кучке, которые окажутся лежащими красной стороной вверх, станет равно ![]() , как и во второй кучке из оставшихся
, как и во второй кучке из оставшихся ![]() фишек.
фишек.
Обучение решению олимпиадных задач по математике — это отдельный навык профессионального репетитора. Умение решать олимпиадные задания по математике необходимо не только в том случае, когда идёт расчёт на поступление в школу 179 с репетитором, но и сильно пригодится ребёнку во взрослой жизни. Ведь известно, что математика — это гимнастика ума. При этом учиться мастерству решения олимпиадных задач по математике лучше с начальной школы. Именно в это время проходит самая активная фаза формирования высших психических функций ребёнка. И от того, насколько хорошо они будут сформированы в этом возрасте, напрямую зависит степень успешности вашего ребёнка во взрослой жизни.
| Пример 9. Идя навстречу трамваям, пешеход встречал их каждые 5 минут, идя с ними в одну сторону — каждые 7 минут. Как часто он будет их встречать, стоя на месте? (Трамваи движутся с постоянной скоростью и с одинаковыми интервалами. Скорость пешехода тоже постоянна). |
Пусть скорость трамвая равна ![]() км/мин., а скорость пешехода
км/мин., а скорость пешехода ![]() км/мин. Тогда при движении пешехода навстречу трамваям скорость их сближения равна
км/мин. Тогда при движении пешехода навстречу трамваям скорость их сближения равна ![]() км/мин., а при движении пешехода в одну сторону с направлением движения трамваев скорость сближения равна
км/мин., а при движении пешехода в одну сторону с направлением движения трамваев скорость сближения равна ![]() км/мин. Поскольку расстояние между трамваями одинакового, то имеет место равенство:
км/мин. Поскольку расстояние между трамваями одинакового, то имеет место равенство:
![]()
Из него получаем, что ![]() . То есть скорость трамвая в 6 раз больше скорости пешехода. Пусть искомое время равно
. То есть скорость трамвая в 6 раз больше скорости пешехода. Пусть искомое время равно ![]() мин. Тогда записанное выше равенство можно дополнить:
мин. Тогда записанное выше равенство можно дополнить:
![]()
С учётом полученного соотношения для скоростей трамвая и пешехода получаем:
![]()
Из последнего равенства находим, что ![]() мин.
мин. ![]() мин.
мин. ![]() с.
с.
Репетитор для поступления в школу 179
Надеюсь, я привёл достаточно примеров того, что занятия с опытным и профессиональным репетитором, знающим специфику вступительных экзаменов в школу 179, помогут вашему ребёнку более эффективно подготовиться к поступлению, с сравнении с другими способами подготовки. В условиях ограниченности во времени поступление в школу 179 с репетитором — это наиболее надёжный способ. Об этом же говорят мои ученики и их родители в своих отзывах. Так что если вам требуется подготовка к вступительному экзамену в школу 179, обращайтесь ко мне за помощью. Я с удовольствием вам в этом помогу. Подробную информацию о моих занятиях вы можете найти на этой странице. Мои контактные данные вы найдёте здесь. Успехов вам в подготовке к вступительному экзамену в школу 179!
Автор статьи: репетитор для поступления в школу 179 в Москве Сергей Валерьевич


Добрый день ! Ребенок 4 класс . Математика отлично. Живем в Жулебино. Планируем поступать в 179 школу. Записались на подготовку в Лицей вторая школа . Но ребенка сильно укачивает. Ездить не можем. Подскажите, пожалуйста , выезжаете ли Вы в наш район ? И с какого класса надо готовится к поступлению в 179 школу?
Добрый день! Я проживаю в районе метро «Тёплый Стан», поэтому в Жулебино выезжать, к сожалению, возможности нет. Могу проводить занятия дистанционно (по скайпу с использованием интерактивной онлайн-доски). Опыт показывает, что это прекрасная альтернатива очным занятиям. Чем раньше начнётся подготовка, тем выше шанс успешно сдать вступительные экзамены. С учениками 4 класса я занимаюсь постоянно, в том числе дистанционно.
Добрый день! Подскажите, пожалуйста, вы занимаетесь с детьми 5 класса? Сколько по времени идёт занятие? Метро Динамо.
Добрый день, да, занимаюсь. С учениками 5 класса обычно по 60 минут. Занятия проходят по скайпу с использованием интерактивной онлайн доски.
Добрый день, меня интересует поступление в инженерный класс, вы готовите?
Добрый день. Да, готовлю. Мои контакты можно найти на этой странице. Напишите мне на электронную почту, и мы согласуем все детали.
Здравствуйте! У меня два вопроса. Сколько задач вы успеваете разобрать с учеником за 60 минут? Как много дз задаете.И есть ли гарантии поступления Здесь вопрос ориентирован на то,как вы сами оцениваете уровень подготовки своих учеников? Спасибо
Речь идет о мальчике, поступление планирует через год в 179 школу.Заканчивает 4й класс.
Добрый день! Чтобы ответить на Ваши вопросы, мне нужно позаниматься с учеником. Посмотреть его текущий уровень, какая база, как он решает задачи, рассуждает, оформляет решение и много другое. Без серьёзного анализа хороший доктор диагноз не поставит. Так и в обучении. Всё очень индивидуально. Домашнее задание задаю после каждого занятия. Опять же, каждому индивидуально. Могу задавать много. Главное, чтобы оно выполнялось. Ученики мне отправляют решение перед следующим занятием, чтобы я успел его проверить. Начинаем занятие всегда с разбора проблем, которые возникли при выполнении д/з. Всё это также учитывается при планировании каждого урока.
Что касается гарантий, то, разумеется, гарантировать стопроцентное поступление я не могу. Я могу гарантировать, что буду проводить качественные занятия с учеником, на которых мы будем учиться решать задачи по математике, подобные тем, которые дают на вступительных экзаменах. И опыт показывает, что если начать подготовку заблаговременно и затратить на это достаточное количество времени и сил, то шансы на поступление существенно возрастают.
Как вы сами оцениваете уровень готовности ваших учеников ,если говорить о школе 179? Цена подготовки составляет полмиллиона рублей,поэтому хочется гарантий.Не те гарантии,когда вы обещаете поступление, а гарантии о том,что уровень готовности мотивированного на учебу ребенка будет достаточен для поступления. Вы знаете,как бывает….Ученик готовится год,а на экзамене оказывается,что внезапно появилась задача из темы, которую не изучали с репетитором и ученик просто не набрал нужный бал. Таким образом,очень важно знать,как учитель сам оценивает уровень готовности своих учеников. Вы считаете,что уровень подготовленности ваших учеников высокий и объем знаний достаточный для поступления в 179 школу?Спасибо!
Все мои ученики, с которыми мы занимаемся основательно и последовательно, демонстрируют существенный прогресс по сравнению с началом обучения. Уровень подготовки многих из них я оцениваю, как очень высокий, и мне всегда приятно, когда моя оценка совпадает с мнением родителей, а также подтверждается успешными результатами на вступительных экзаменах, в том числе в школу 179.
Смотрю на ёмкости. Из 9-5=4. Остаток в 9 литровом. Теперь сливаем в 14 литровый 9+4=13. Далее выливаем из 13 литров 5. 13-5=8. Осталось слить куда-то ещё литр. Выливаем из 9 литрового 5 литров, оставляем 4. 5 литровый снова осврбождаем и заливаем туда 4 литра. В 5 литровом не хватает литра до 5. Как раз этот литр и берём из тех 8, что у нас осталось в 14 литровом бочке. По моему так быстрее? Ещё раз: 9-5 =4, слили в 14 литровый. 9+4=13. 13-5=8. 9-5 =4. Сливаем 4 в 5 литровый. И из 14 литрового, где у нас хранится 8 литров, один литр доливаем в 5 литровый. Остаётся 7 литров. Но ребенок скорее всего будет тупить. По сути вообще пофиг какой объем первого бочка, если >=13. Мое решение быстрее .
Задачки классные! Мне нравятся. Надо проэкспериментировать на своем второклашке. Но он тупит сильно. 2*2 и весенний Олимп вообще не прошел отборочный тур. Мне все нравится, особенно люблю в объяснениях иллюстрации, но 5 косарей за одно занятие это капец, товарищи…
Я вот читаю комментарий «математика — отлично». И думаю, а зачем тогда репетитор? Вот как раз не отлично. Или про отметки в школе? Если про отметки, дык вообще не показатель. Сыну частенько «4» ставят и пишут комментарий «мы это ещё не проходили», «мы таким способ ещё не решали». А его прижимаю к себе и спрашиваю, понятен ли ему тот вариант, которым он посчитал или нет. Если понятен, то вытри сопли, продолжай делать также. А учитель максимум «4» поставит. И отметки — это вообще ерунда. Быть отличником по математиматике в школе, потому что решаешь задачи строго по шаблону — это наоборот вредно. Так что в некоторых случаях не быть отличником куда почетнее. Другое дело, хочется, чтобы ребенок учителя уважал. А как его уважать, если его не уважает твоя мать? Есть учительница в нашей школе, которая просто свет в окошке, но она ведёт старший класс. К ней никак. Мы сейчас сменили учителя. Я год билась, чтобы поменять. Лучше, не спорю, но все равно мрак. Теперь думаю школу поменять. Почему в нормальных школах учат по Петерсон, а в нашей … Ну, вы поняли, не по Петерсон. Это какое-то гнусное издевательство над детьми. Времени и так не хватает со всеми кружками, а ты вынужден ещё дома второй учебник проходить по каждому предмету (ну, кроме физры, музыки и природоведения, окружающего мира по новому).
Здравствуйте! Как записаться на ваши занятия?
Здравствуйте, напишите мне на почту (seliverstov@yourtutor.info) или в WhatsApp, Viber (+7-964-562-94-19). Мы подберём удобное время для занятий.
Добрый день, а вы гарантию можете дать, что ребёнок поступит в 179 школу если будет заниматься у вас
Добрый день. Негласный кодекс профессиональной этики преподавателя не позволяет давать такие гарантии.