Поступление в гимназию 1543 – шаг к успеху и инвестиция в будущее. Многие родители из Москвы хотели бы отдать сюда ребёнка на обучение благодаря высокому уровню образования, богатой внеклассной жизни. Учреждение славится безупречной репутацией, педагоги имеют заслуженные награды и звания. Здесь учились многие известные люди. Гимназия была открыта в 1975 в новом районе города, изначально имела статус обычной московской школы. Престижное звание учреждение получило в 1994. Сегодня это одно из самых достойных учебных заведений столицы для школьников 5-11 классов, гордящееся своими достижениями и высокими позициями в различных рейтингах качества школьного образования.
Поступление в гимназию 1543 – шаг к успеху и инвестиция в будущее. Многие родители из Москвы хотели бы отдать сюда ребёнка на обучение благодаря высокому уровню образования, богатой внеклассной жизни. Учреждение славится безупречной репутацией, педагоги имеют заслуженные награды и звания. Здесь учились многие известные люди. Гимназия была открыта в 1975 в новом районе города, изначально имела статус обычной московской школы. Престижное звание учреждение получило в 1994. Сегодня это одно из самых достойных учебных заведений столицы для школьников 5-11 классов, гордящееся своими достижениями и высокими позициями в различных рейтингах качества школьного образования.
В учреждении открыто 4 специализации по профилям (с 8 класса):
- математическому;
- гуманитарному;
- физико-химическому;
- биологическому.
Учебный процесс частично похож на занятия в институте. На базе школы организуются научно-практические конференции, ученики активно участвуют в образовательной и внеурочной деятельности, занимаются написанием курсовых работ, и даже вместо привычной учительской здесь – кафедры. Кроме основных предметов подростки излучают дополнительные курсы, занимаются в специально организованных мастерских, кружках и секциях. Ученики периодически путешествуют по стране и выезжают за границу.
Что нужно знать про поступление в гимназию 1543
 Учебный процесс в гимназии состоит из трёх ступеней: среднего образования (5-7 класс), основного общего образования (8 – 9 класс) и полного общего образования (10 – 11 класс). Поступить в учреждение может любой ребёнок, проживающий в Москве. При этом из-за высокого конкурса каждый поступающий обязан сдать вступительные экзамены в устной и письменной форме, причём довольно сложные (примеры вступительных в 8 класс вы можете найти в этой, этой и этой статьях). Поэтому перед каждым родителем, решившим поступать в гимназию 1543, встаёт вопрос, как организовать подготовку ребёнка к вступительным экзаменам.
Учебный процесс в гимназии состоит из трёх ступеней: среднего образования (5-7 класс), основного общего образования (8 – 9 класс) и полного общего образования (10 – 11 класс). Поступить в учреждение может любой ребёнок, проживающий в Москве. При этом из-за высокого конкурса каждый поступающий обязан сдать вступительные экзамены в устной и письменной форме, причём довольно сложные (примеры вступительных в 8 класс вы можете найти в этой, этой и этой статьях). Поэтому перед каждым родителем, решившим поступать в гимназию 1543, встаёт вопрос, как организовать подготовку ребёнка к вступительным экзаменам.
Существует несколько способов подготовки к вступительным экзаменам. Самый простой, не требующий финансовых вложений, – самостоятельная подготовка ребёнка по методическим пособиям, в том числе с помощью родителей. Этот метод отличается низкой эффективностью. Отсутствует грамотно составленный план занятий, который позволяет готовиться к экзаменам и не забывать про текущие домашние задания. У взрослых также нет профессионального представления о том, что конкретно будет ждать школьника на вступительных экзаменах. Родителям, не имеющим опыта, трудно мотивировать сына или дочь на учёбу. При изучении сложной темы часто возникают вопросы и проблемы, справиться с которыми под силу только специалисту.
Популярностью стало пользоваться также посещение кружков по математике и физике. Занятия проходят в формате мини-урока, только класс состоит не из 30, а из 10 – 15 человек. Преимущества этого способа в том, что знания слушателям даёт педагог, который хорошо ориентируется в теме, может моментально ответить на любой вопрос. Однако существенный минус – отсутствие индивидуального подхода. Учитель работает с группой, давая усреднённые задания, без учёта проблем и потребностей каждого конкретного ученика. Это приводит к тому, что отстающие дети не успевают за теми, кому предмет даётся легче. Страдают и лидеры, вынужденные постоянно ждать товарищей, подстраиваться под их более низкую планку.
Наиболее эффективный вариант – поступление в гимназию 1543 с репетитором. Это самая удобная, продуктивная и спокойная для ребёнка форма работы. Школьник сам задаёт себе темп умственных тренировок, ему не нужно никого ждать или догонять. Метод ценен и за другие достоинства:
- каждая минута урока посвящена исключительно вашему ребёнку;
- родители могут ставить репетитору конкретные задачи и контролировать прогресс;
- удобный график занятий.
Как показывает практика, именно занятия с профессиональным репетитором являются наиболее эффективным способом подготовки к поступлению в гимназию 1543. При этом важно помнить, что для того, чтобы поднять уровень знаний, научиться решать сложные задачи и получить высокие баллы на экзамене, стоит обращаться к специалисту с хорошей репутацией и отзывами, имеющему качественное профильное образование, а также большой опыт подготовки к поступлению в гимназию 1543.
Помощь репетитора при поступлении в гимназию 1543
Я предлагаю москвичам услуги профессионального репетитора. Закончив факультет физики и информационных технологии в МПГУ, я полностью посвятил себя работе с детьми и подростками. Сегодня я преподаю в ВУЗе, провожу частные уроки по математике и физике.
Опыт беспрерывной с 2008 года работы позволяет мне найти подход к любому, в том числе неусидчивому, медлительному, неуверенному в себе ребёнку. Занимаясь со мной, вы быстро увидите положительный результат, потому что я:
- использую удачное сочетание традиционных и современных методик преподавания;
- имею собственную наработку дидактических материалов;
- имею за плечами огромный опыт подготовки школьников к вступительным экзаменам, в том числе в гимназию 1543;
- провожу свои уроки в удобное для ребёнка время;
- могу организовать постоянные или периодические занятия по Skype с использованием интерактивной доски.
Когда я беру нового ученика, прежде всего я беседую с родителями, выслушиваю их мнение и пожелания. На первых уроках я тестирую подростка, выясняя, какой у него уровень знаний и умений, в каких темах есть пробелы.
На занятиях мы на глубоком уровне изучаем математику и физику, учимся решать простые и сложные задачи, готовимся к олимпиадам по математике и физике, занимаемся повышением текущей успеваемости ученика в школе, а также готовимся к устным и письменным вступительным экзаменам, в том числе в Московскую гимназию на Юго-Западе № 1543. Я регулярно оцениваю результаты обучения, обсуждаю их с родителями с целью достичь наилучших результатов обучения. После занятий со мной ученик:
- на глубоком уровне будет понимать все темы школьной программы;
- научится решать сложные задачи по математике и физике;
- приобретёт уверенность в себе;
- потренируется в решении вариантов вступительных экзаменов в гимназию 1543 прошлых лет;
- заинтересуется предметом.
Обеспечьте себе поступление в гимназию 1543 с репетитором. Свяжитесь со мной по телефону или email, я помогу вашему ребёнку получить высокий балл на вступительных экзаменах в гимназию 1543 и занять своё место в одной из престижнейших гимназий столицы.
Ну и чтобы не быть голословным, предлагаю вам разобрать несколько заданий, подобных тем, которые встречаются на вступительных экзаменах в гимназию 1543. Оцените сложность этих заданий и попробуйте решить их самостоятельно.
Поступление в гимназию 1543 с репетитором (5 класс)
Пример 1. В классе 30 человек. Известно следующее:
Каких учеников больше: тех, кто принёс циркуль или тех, кто принёс линейку, но забыл циркуль? |
С первого взгляда может показаться, что задача запутанная и непонятная. Для многих учеников младших классов из обычных среднестатистических школ это действительно так, ведь их попросту не учат решать такие задачи. Но на самом деле решение здесь очень простое, особенно если раньше уже сталкивался с подобными задачами, например, на уроках с репетитором.
- Поскольку известно, что циркуль забыли 18 человек из 30, значит, с циркулем на урок пришли 12 человек. По условию известно, что они же принесли и линейки.
- Поскольку забыли линейки 8 человек из 30, что с линейкой на уроке сидит 22 ученика. Из них, как мы выяснили, 12 ещё и с циркулем. Значит, 10 человек принесли линейку, но забыли циркуль.
- Итак, учеников, которые принесли циркуль больше, чем учеников, которые принесли линейку, но забыли циркуль.
Вот такое решение. Главное не «заблудиться в трёх соснах». Разберём ещё один пример.
| Пример 2. В 5А классе в шахматы умеет играть половина мальчиков и треть девочек. При этом четверть всех шахматистов класса — девочки. Сколько детей в 5А классе, если в шахматы умеют играть 12 человек? |
- Четверть от всех учеников в классе, которые умеют играть в шахматы, составляют 3 человека. И по условию это девочки.
- Известно также, что в шахматы умеет играть треть всех девочек в классе. То есть всего в классе 9 девочек.
- Поскольку четверть всех шахматистов класса — девочки, то три четверти — мальчики. Как мы уже выяснили, четверть всех шахматистов составляют 3 человека. Значит, три четверти — это 9 человек. И это мальчики.
- По условию шахматисты-мальчики составляют половину мальчиков класса. То есть в классе 18 мальчиков.
- Итак, общее число учеников в классе равно 18 + 9 = 27 человек.
Ответ: 27 человек.
| Пример 3. Петя раскрасил грани куба в красный и синий цвета. Докажите, что у этого куба обязательно найдётся такое ребро, которое смыкает две грани одного цвета. |
Возьмём любую вершину куба. В ней сходятся три грани куба:
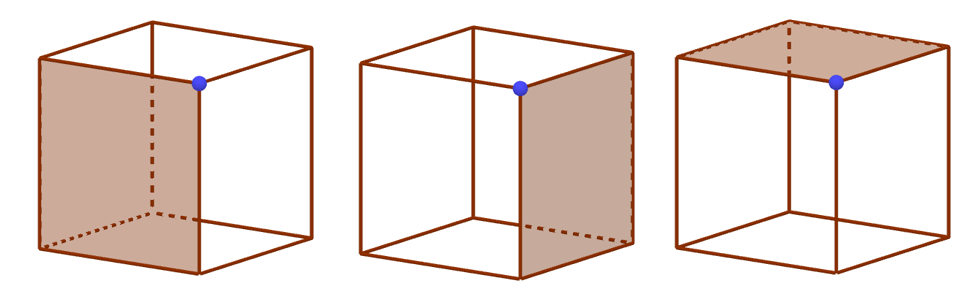
Значит, две грани из этих трёх обязательно будут одного цвета. Именно они и будут сходиться на ребре, исходящем из этой вершины.
Поступление в гимназию 1543 с репетитором (8 класс)
| Пример 1. Иннокентий записал в ряд по возрастанию все 16 натуральных делителей некоторого натурального числа N. Чему оказалось равно произведение пятого и двенадцатого члена в этом ряду? |
Записанный Иннокентием ряд должен выглядеть следующим образом:
1, D2, D3, D4, D5, D6, D7, D8, D9, D10, D11, D12, D13, D14, D15, N
Первое число в этом ряду — обязательно 1, последнее — обязательно N, поскольку минимальный делитель любого натурального числа — это 1, максимальный — само это число. Значит, произведение первого и последнего чисел в записанном ряду равно N: D1 × D16 = 1 × N = N.
Но это же можно сказать и о произведении второго члена ряда с предпоследним. Оно тоже равно N. Действительно, D2 — наименьший из делителей числа N, отличный от 1. Значит, если разделить N на D2, то получится наибольший делитель числа N, отличный от самого этого числа. То есть D2 × D15 = D2 × N : D2 = N.
Аналогично доказывается, что D3 × D14 = N, D4 × D13 = N и D5 × D12 = N. Итак, произведение пятого и двенадцатого числа в записанном ряду равно N.
| Пример 2. Первый поезд длиной 450 м движется со скоростью 40 км/ч. Навстречу ему со скоростью 60 км/ч движется второй поезд длиной 550 м. Каково расстояние от точки, где встретятся начала этих поездов до точки где встретятся концы этих поездов? |
- Поезда сближаются со скоростью: 60 км/ч + 40 км/ч = 100 км/ч. При этом суммарная длина поездов равна: 450 м + 550 м = 1 км. Значит, время, в течение которого один поезд будет проезжать мимо другого, равно: 1 км / 100 км/ч = 0.01 ч.
- За это время конец первого поезда переместится на расстояние: 40 км/ч × 0.01 ч = 0.4 км = 400 м, то есть не доедет до места встречи начал поездов 50 м (так как длина первого поезда 450 м).
- Аналогично, конец второго поезда переместится на расстояние: 60 км/ч × 0.01 ч = 0.6 км = 600 м, то есть окажется на 50 м дальше от места встречи начал поездов в сторону своего движения (так как его длина равна 550 м).
- Итак, конца поездов окажутся на расстоянии 50 м от точки встречи начал поездов.
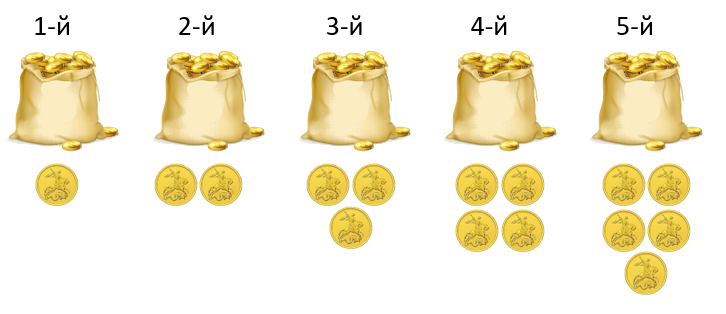
| Пример 3. Имеется 5 мешков, набитых одинаковыми по внешнему виду золотыми монетами. Известно, что все монеты в одном из мешков фальшивые. Вместо положенных 100 г они весят лишь 99 г. Как за одно взвешивание на электронных весах определить, в каком мешке находятся фальшивые монеты? |
Нужно взять из первого мешка одну монету, из второго — две, из третьего — три и так далее. Из пятого мешка, соответственно, нужно взять пять монет:
Взвешиваем все монеты на весах. Если бы все монеты были настоящими, то весы показали бы: 100 г × (1+2+3+4+5) = 1500 г. Поскольку среди монет есть фальшивые, то суммарный вес будет несколько меньше. Если в наборе одна фальшивая монета, то вес будет отличаться от 1500 г на 1 г, если две — на 2 г, если 3 — на 3 г и т. д. Значит, на сколько граммов полученный вес будет отличаться от 1500 г, в том по порядку мешке и находятся фальшивые монеты.
Как поступить в гимназию 1543
Если вам требуется подготовка к вступительному экзамену в гимназию 1543 в Москве, обращайтесь ко мне. Я занимаюсь подготовкой школьников к поступлению в это учебное заведение на протяжении многих лет и прекрасно осведомлён о всех нюансах и особенностях процесса подготовки к вступительным экзамена в гимназию 1543, а также их сдачи. Начинать подготовку нужно заблаговременно, особенно если у ребёнка есть проблемы с освоением математики, в том числе с решением сложных и олимпиадных задач. Помните, что для качественной подготовки требуется немало времени. Обеспечьте себе поступление в гимназию 1543 с репетитором. Мои контакты вы можете найти на этой странице. Успехов вам в подготовке к поступлению в гимназию 1543!
Материал подготовил репетитор для поступления в гимназию 1543 в Москве, Сергей Валерьевич
Понравилась статья? Возможно, вам будут интересны также следующие: