В данной статье представлен разбор демонстрационного варианта вступительного экзамена по физике в Московскую гимназию №1543 на Юго-Западе. Сам вариант можно найти на официальном сайте гимназии. Если вас интересует разбор вступительного экзамена по математике, вы можете найти его на данной странице. Обе статьи написаны профессиональным репетитором, который занимается подготовкой к поступлению в гимназию 1543 по физике и математике.
Разбор варианта экзамена по физике для подготовки к поступлению в гимназию 1543
| 1. Что общего между слипанием листов бумаги, пайкой и сваркой металлов? Что различного? Объясните подробно на основе представления о молекулах. |
- Слипание листов бумаги может происходить в случае, если они, например, смочены водой. В этом случае вода занимает пространство между бумагой так, что расстояние между молекулами воды и молекулами бумаги становится достаточно малым, чтобы начали играть существенную роль силы межмолекулярного притяжения.
- Пайка — это процесс соединения твёрдых материалов с помощью припоя. При пайке происходит взаимное растворение и диффузия основного материала и припоя, который заполняет зазор между соединяемыми частями изделия. При этом диффузии молекул соединяемых материалов не происходит.
- Сварка — это процесс установления межмолекулярных связей между соединяемыми материалами. При сварке происходит диффузия молекул свариваемых материалов. Сварка происходит при высокой температуре или давлении.
Общее во всех трёх процессах состоит в том, что соединение между материалами во всех случаях устанавливается за счёт межмолекулярного притяжения. Различие состоит в том, что при сварке происходит диффузия молекул соединяемых материалов, при пайке — диффузия молекул каждого соединяемого материала с материалом припоя, при склеивании — диффузия не играет существенной роли.
| 2. Покупатель хочет купить на рынке килограмм изюма, причём выясняется, что у продавца неисправны весы: при размещении на чашах двух килограммовых гирь одна из чаш перевешивает. Предложите способ точного взвешивания гирь. Предложите способ точного взвешивания килограмма изюма, чтобы в убытке не оказался ни покупатель, ни продавец. Внутреннее строение весов считается недоступным. Гири массой менее килограмма отсутствуют. |
Из сказанного в условии можно предположить, что эти чашечные весы сбиты из-за неодинакового расстояния от чашек до центра весов. В этой ситуации нужно поступить следующим образом:
- Разместить на каждой чаше весов по одной килограммовой гире. Равновесие весов будет нарушено.
- Насыпать изюм на чашу противоположную той, которая перевешивает, до наступления равновесия. Тогда гири будут уравновешены.
- Убрать гирю с чаши, в которой нет изюма, и насыпать в эту чашу изюм до тех пор, пока вновь не наступит равновесие.
- Отсыпанная во второй раз часть изюма будет весить 1 кг.
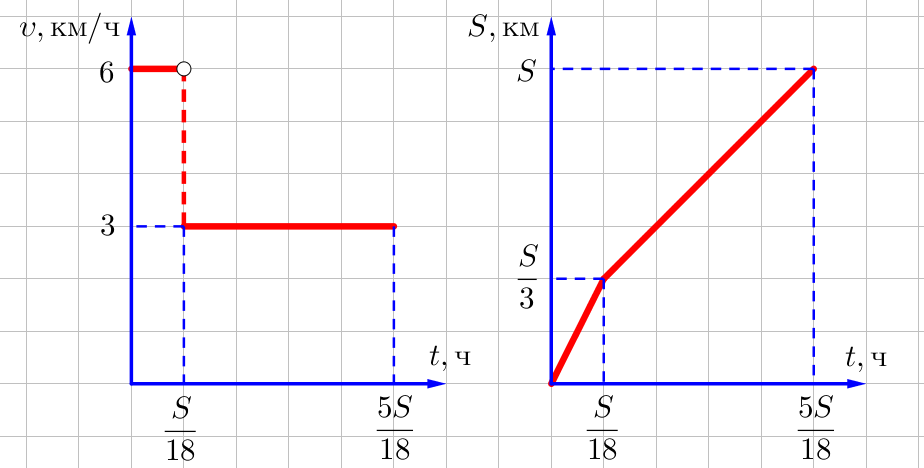
| 3. Первую треть пути турист шёл по шоссе со скоростью 6 км/ч, а остальной путь — через бурелом со скоростью 3 км/ч. Определите среднюю скорость туриста и постройте графики зависимости скорости от времени и пути от времени. |
Пусть общий путь равен ![]() км, а общее время движения равно
км, а общее время движения равно ![]() ч. Тогда искомая средняя скорость равна
ч. Тогда искомая средняя скорость равна ![]() км/ч. При этом время движения туриста на первой трети пути равно
км/ч. При этом время движения туриста на первой трети пути равно ![]() ч, где
ч, где ![]() км/ч — скорость движения туриста по шоссе, а время движения туриста на остальном пути равно
км/ч — скорость движения туриста по шоссе, а время движения туриста на остальном пути равно ![]() ч, где
ч, где ![]() км/ч — скорость движения туриста по второй части пути (по бурелому). То есть время движения по первому участку пути в 4 раза меньше времени движения по второму участку. Тогда с учётом того, что
км/ч — скорость движения туриста по второй части пути (по бурелому). То есть время движения по первому участку пути в 4 раза меньше времени движения по второму участку. Тогда с учётом того, что ![]() получаем следующее выражение для средней скорости движения:
получаем следующее выражение для средней скорости движения:
![Rendered by QuickLaTeX.com \[ u=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{3\upsilon_1}+\frac{2S}{3\upsilon_2}}=\frac{3\upsilon_1\upsilon_2}{2\upsilon_1+\upsilon_2}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ff7d71a8fe9391ff24e3f90d1c3f0efc_l3.png)
Расчёты дают значение средней скорости ![]() км/ч.
км/ч.
При этом общее время движения равно ![]() ч. Тогда графики скорости и пути от времени должны выглядеть следующим образом:
ч. Тогда графики скорости и пути от времени должны выглядеть следующим образом:
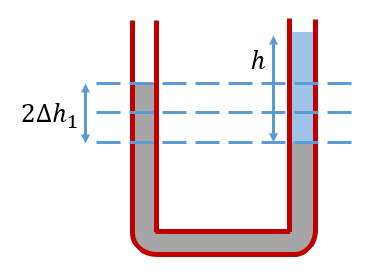
| 4. В U-образной трубке налита ртуть, в одно колено трубки доливают столб воды высотой 26.2 см. Насколько повысится при этом уровень ртути во втором колене? Плотность ртути 13600 кг/м3. Как бы изменилось решение задачи, если бы площадь сечения трубки, в которую наливали воду, была в 4 раза больше, чем у второй трубки? |
После того, как в одно из колен U-образной трубки нальют воду, уровень ртути в этом колене понизится на величину ![]() . Поскольку ртуть практически несжимаема, и её объём не меняется, а площадь сечения трубки одинакова по всей её длине (в первом случае), то на такую же высоту поднимется уровень ртути в другом колене. Тогда разница уровней ртути в обоих сосудах составит
. Поскольку ртуть практически несжимаема, и её объём не меняется, а площадь сечения трубки одинакова по всей её длине (в первом случае), то на такую же высоту поднимется уровень ртути в другом колене. Тогда разница уровней ртути в обоих сосудах составит ![]() :
:
Поднятие прекратится, когда гидростатические давления в правом и левом коленах U-образной трубки уравняются. То есть будет иметь место равенство:
![]()
Здесь ![]() кг/м3 — плотность воды,
кг/м3 — плотность воды, ![]() кг/м3 — плотность ртути,
кг/м3 — плотность ртути, ![]() см — высота столба воды. Расчёты дают результат
см — высота столба воды. Расчёты дают результат ![]() см.
см.
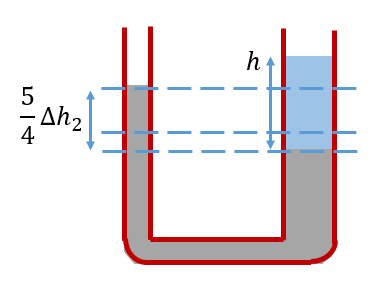
В асимметричной U-образной трубке изначальный уровень ртути всё равно будет одинаковым, что следует из закона сообщающихся сосудов. Однако, поскольку площадь сечения трубки, в которую наливали воду, в 4 раза больше, то при поднятии уровня ртути в другом колене на ![]() , уровень ртути в колене с водой опустится на
, уровень ртути в колене с водой опустится на ![]() , так как объём ртути остаётся неизменным. То есть разница уровней ртути в сосудах составит уже
, так как объём ртути остаётся неизменным. То есть разница уровней ртути в сосудах составит уже ![]() :
:
Тогда уравнение баланса давлений будет иметь вид:
![]()
Расчёты дают в этом случае ![]() см.
см.
| 5. На дне сосуда, заполненного 100 г спирта, лежит пластмассовая деталь. Сколько воды надо добавить в сосуд, чтобы деталь всплыла? Плотность спирта 800 кг/м3, плотность используемой пластмассы 850 кг/м3. |
Пусть ![]() г — масса спирта,
г — масса спирта, ![]() кг/м3 — плотность спирта,
кг/м3 — плотность спирта, ![]() кг/м3 — плотность пластмассы,
кг/м3 — плотность пластмассы, ![]() кг/м3 — плотность воды.
кг/м3 — плотность воды.
Очевидно, предполагается, что спирт смешивается с водой. При этом придётся пренебречь эффектом уменьшения объёма при смешивании спирта и воды. Скорее всего, авторы задачи просто не учли этот момент. Иначе в условии задачи они должны были указать, как соотносятся объём раствора спирта в воде и суммарный объём обоих компонентов. В любом случае, этот эффект не рассматривается в школьном курсе физики 7 класса, поэтому проверяющий не в праве снизить за это баллы.
Для того, чтобы деталь всплыла, потребуется влить в спирт ![]() кг воды. Тогда в момент, когда деталь начнёт всплывать, сила Архимеда, действующая на неё, станет равной силе тяжести. Иными словами, плотность вещества, из которого изготовлена деталь, станет равной плотности раствора спирта в воде, в котором эта деталь находится. Тогда имеет место следующее равенство:
кг воды. Тогда в момент, когда деталь начнёт всплывать, сила Архимеда, действующая на неё, станет равной силе тяжести. Иными словами, плотность вещества, из которого изготовлена деталь, станет равной плотности раствора спирта в воде, в котором эта деталь находится. Тогда имеет место следующее равенство:
![Rendered by QuickLaTeX.com \[ \rho=\frac{m_0+m_1}{V_0+V_1}=\frac{m_0+m_1}{\frac{m_0}{\rho_0}+\frac{m_1}{\rho_1}}=\frac{\rho_0\rho_1(m_0+m_1)}{m_0\rho_1+m_1\rho_0}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-54e3b3289cdb163cda1190815bb41155_l3.png)
Здесь ![]() — объём влитой воды,
— объём влитой воды, ![]() — объём спирта. Если учитывать эффект уменьшения объёма, то в знаменателе нужно ещё ввести соответствующий коэффициент.
— объём спирта. Если учитывать эффект уменьшения объёма, то в знаменателе нужно ещё ввести соответствующий коэффициент.
Теперь осталось выразить из данной формулы ![]() . Для этого выражаем числитель, раскрывая при этом все скобки:
. Для этого выражаем числитель, раскрывая при этом все скобки:
![]()
Переносим в левую сторону уравнения все слагаемые, содержащие множитель ![]() , и выносим его за скобки. Остальные слагаемые переносит в правую сторону равенства и также выносим общий множитель за скобку:
, и выносим его за скобки. Остальные слагаемые переносит в правую сторону равенства и также выносим общий множитель за скобку:
![]()
Выражая теперь из полученной формулы искомый множитель ![]() , получаем окончательный результат:
, получаем окончательный результат:
![]()
Для красоты, чтобы не получалось отрицательных чисел в числителе и знаменателе, можно поменять в них знаки:
![]()
Расчёты дают значение ![]() г.
г.
| 6. Объясните существование времён года на Земле. Всегда ли на планете должны существовать времена года? |
Земля вращается вокруг Солнца по эллиптической траектории. Однако, она очень мало отличается от окружности. Поэтому объяснить смену времён года тем, что Земля находится на разном расстоянии от Солнца в разное время в течение года и получает в точке наибольшего отдаления от Солнца существенно меньшее количество энергии, чем в точке наибольшего приближения, нельзя.
Истинная причина смены времён года на Земле состоит в том, что ось суточного вращения Земли наклонена к плоскости орбиты Земли вокруг Солнца.
В результате в разных точках этой орбиты длительность светового дня в Северном и Южном полушарии Земли различна (зимой в Северном полушарии короче, а в Южном длиннее, летом — наоборот). Кроме того, Северное и Южное полушария в разных точках орбиты Земли освещаются Солнцем с разной интенсивностью из-за изменения угла падения солнечных лучей на земную поверхность. Когда интенсивность освещения максимальна в Северном полушарии, то в Южном полушарии она, напротив, минимальна. И наоборот. В результате зима в Северном полушарии совпадает с летом в Южном. И наоборот.
То есть на планете не будет времен года, если:
- Ось её суточного вращения перпендикулярна (или почти перпендикулярна) плоскости её орбитального движения вокруг звезды, относительно которой она вращается.
- Форма орбиты планеты не представляет собой сильно вытянутый эллипс (максимально близка к окружности).
Контакты репетитора для подготовки к поступлению в гимназию 1543 по физике и математике
Если вас интересует подготовка к поступлению в гимназию 1543 по физике или математике, рекомендуем обратиться к профессиональному репетитору в Москве Сергею Валерьевичу. Возможны очные и дистанционные занятия.
Понравилась статья? Возможно, вам также будет интересна следующая: