В данной статье представлен разбор варианта письменной работы по математике для поступающих в 8-е классы естественнонаучного профиля Московской гимназии №1543 на Юго-Западе. Если вас интересует поступление в математический класс, разбор соответствующего демонстрационного варианта письменной работы вы можете найти на этой странице. Если же вы поступаете по профилю «Физика», то разбор варианта вступительного экзамена по физике находится здесь. Все статьи написаны профессиональным репетитором по математике и физике, который занимается подготовкой школьников к поступлению в гимназию 1543.
Разбор варианта письменной работы по математике в гимназию 1543
| 1. Упростите:
|
Это вполне стандартное школьное задание по математике на знание свойств степеней. С его решением обязан справиться любой школьник, если он планирует поступать в Московскую гимназию №1543 на Юго-Западе. Итак, используя свойства возведения степени в степень, преобразуем данное выражение:
![Rendered by QuickLaTeX.com \[ \left(-\frac{5}{2}a^3b\right)^4\cdot \frac{16}{5}a^8b^5 =\frac{5^4}{2^4}a^{12}b^4\cdot \frac{2^4}{5}a^8b^5. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5f8cb9cc4aa2b811a7200c879e7cc230_l3.png)
Далее используем свойство умножения степеней с одинаковыми основаниями:
![]()
| 2. Разложите на множители:
|
Это также вполне типичное задание на преобразование выражений и разложение их на множители. Для его решения нужно владеть навыками сложения и умножения многочленов, знать формулы сокращённого умножения, а также уметь раскладывать многочлены на множители методом вынесения общего множителя за скобки. А главное, делать всё это без ошибок в вычислениях. Большое количество школьников, к сожалению, допускают при решении таких заданий много ошибок из-за невнимательности. Задача репетитора состоит в том, чтобы указывать на эти ошибки и не допускать их возникновения в будущем.
Итак, раскрываем скобки в выражении, используя формулы сокращённого умножения («разность квадратов» и «квадрат суммы»):
![]()
Далее приводим подобные слагаемые в полученном выражении и выносим общий множитель за скобки:
![]()
| 3. Решите уравнение:
|
Наиболее типичная ошибка школьников при решении уравнений данного вида состоит в том, что они забывают, что минус между первыми двумя дробями относится ко всему числителю второй дроби, а не только к неизвестному. В результате при преобразованиях возникает ошибка, связанная с неверным знаком слагаемых в выражении. Одна маленькая ошибочка, следствием которой становится крах всего решения. Задача репетитора состоит в том, чтобы предостеречь ученика от подобных ошибок на экзамене. Опытный репетитор всегда знает на что в первую очередь обратить внимание своих учеников.
Итак, упростим данное уравнение. Для этого умножим обе его части на наименьшее общее кратное всех знаменателей. То есть на число 60. В результате получаем следующее равносильное уравнение:
![]()
Раскрываем все скобки:
![]()
Переносим все слагаемые, содержащие неизвестное, в левую часть уравнения, а не содержащие — в правую. При этом учитываем, что при переносе слагаемого через знак равенства нужно поменять знак слагаемого на противоположный:
![]()
![]()
| 4. В сосуде было 400 мл 80%-го (по объёму) водного раствора спирта. В сосуд долили литр чистого спирта и литр воды. Определите процентное содержание спирта в полученном растворе. |
Строго говоря, при смешивании спирта с водой наблюдается уменьшение их объема. Я уже писал об этом в статье с разбором вступительного экзамена по физике. Однако, этот эффект, по-видимому, не брался в расчёт авторами задачи. Поэтому мы его также рассматривать не будем. В конце концов это экзамен по математике, а не по химии, поэтому проверяющий не в праве снизить оценку в такой ситуации.
Итак, решаем задачу. В исходном растворе содержалось 400×0.8 = 320 мл спирта и 400-320 = 80 мл воды. После того, как в раствор долили литр спирта и литр воды, воды в растворе стало 1000+80 = 1080 мл, а спирта — 1000+320 = 1320 мл. Тогда искомое процентное содержание спирта в полученном равенстве равно:
![]()
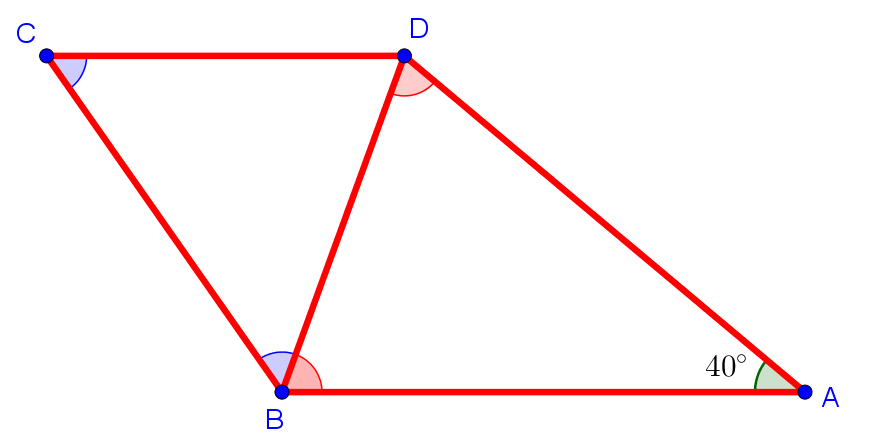
| 5. В четырёхугольнике ABCD сторона AB параллельна стороне CD, AB = AD, BD = CD. Угол BAD равен 40 градусам. Найдите остальные углы четырёхугольника. |
Геометрия — это ахиллесова пята многих школьников, особенно тех, кто собирается поступать в естественнонаучные классы. Может быть поэтому авторы-составители данного варианта письменной работы по математике в гимназию 1543 решили ограничиться достаточно простой задачей по геометрии. Хотя и для её решения от поступающих требуется знание свойств равнобедренного треугольника, теоремы о сумме углов в треугольнике, а также теоремы о сумме односторонних углов при параллельных прямых. Набор знаний, которым обладает далеко не каждый семиклассник.
По определению треугольник ABD — равнобедренный с основанием BD. То есть ∠ABD = ∠ADB. То есть каждый из этих углов равен по 70°, потому что сумма внутренних углов любого треугольника (в нашем случае — треугольника ABD) равна 180°. ∠СDA + ∠BAD = 180°, так как эти углы являются односторонними при параллельных прямых AB, CD и секущей AD. То есть ∠СDA = 140°, а ∠СDB = ∠СDA — ∠BDA = 70°. Тогда в равнобедренном треугольнике CBD получаем ∠BCD = ∠CBD = 55°. Итак, в нашем четырёхугольнике ∠A = 40°, ∠B = 125°, ∠C = 55°, ∠D = 140°.
| 6. В многоквартирном доме на каждом этаже 4 квартиры. Квартира №65 находится на 3-ем этаже, а квартира №125 — в 3-ем подъезде. В каком подъезде и на каком этаже расположена квартира №200? |
Это последняя задача из варианта письменной работы по математике в гимназию 1543. Именно баллы за её решение могут определить исход поступления абитуриента в гимназию. Всегда нужно помнить, что желающих поступить очень много, и конкуренция возникает очень плотная. Поэтому данную задачу нужно решать обязательно. И решать правильно.
К решению данной задачи приводят следующие рассуждения:
- Начнём с того, что в доме не может быть меньше 11 этажей. В противном случае общее количество квартир в 3-х первых подъездах будет не более 120, что противоречит тому, что квартира №125 находится в 3-ем подъезде. Одновременно, в доме не может быть больше 15 этажей. В противном случае общее количество квартир в 2-х первых подъездах будет не менее 128, что также противоречит тому, что квартира №125 находится в 3-ем подъезде. То есть в доме может быть от 11 до 15 этажей.
- То есть в каждом подъезде находится от 44 до 60 квартир. Значит, квартира №65 находится во 2-ом подъезде. Действительно, в 1-ом подъезде она находиться не может, поскольку количество квартир в 1-ом подъезде не более 60. В 3-ем и последующих подъездах она также находиться не может, поскольку минимальное количество квартир в 1-ом и 2-ом подъезде вместе равно 88.
- Число 65 при делении на 4 даёт 16 и в остатке 1. То есть перед квартирой №65 находится 16 полных групп по 4-е квартиры, расположенных на соответствующих этажах в 1-ом и 2-ом подъездах. При этом квартира №65 расположена во 2-ом подъезде на 3-м этаже. Это значит, что в доме 14 этажей. Действительно, в этом случае 14 этажей в 1-ом подъезде плюс 2 этажа во 2-ом подъезде дают вместе 16 полных групп по 4-е квартиры. В 17-ой такой группе (на 3-ем этаже 2-го подъезда) расположена квартира №65.
- То есть в каждом подъезде находится по 56 квартир. 200 при делении на 56 даёт 3 и остаток 32. 32 нацело делится на 4, получается 8. Это значит, что квартира №200 находится в 4-ом подъезде на 8-ом этаже.
Подготовка к письменной работы по математике в гимназию 1543
Вот такие задачи предлагаются школьникам при поступлении в вариантах письменной работы по математике в гимназию 1543. Если при решении данных задач у вас возникли сложности, хотя бы с какой-нибудь из них, это прямое указание, что без серьёзной подготовки поступить в гимназию вам не удастся. И лучше всего в этом отношении подходят индивидуальные занятия с профессиональным репетитором, специализирующимся на подготовке школьников к поступлению в Московскую гимназию №1543 на Юго-Западе по математике и физике. Удачи в подготовке и успехов на экзамене!
Понравилась статья? Возможно, вам также будут интересны следующие:


![Rendered by QuickLaTeX.com \[ \left(-2\frac{1}{2}a^3b\right)^4\cdot 3\frac{1}{5}a^8b^5. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ee7ea618419f217e7fe63aab444cb658_l3.png)
Спасибо