
На днях лицей ВШЭ объявил дополнительный набор школьников на вакантные места. Вместе с этим были опубликованы демонстрационные варианты комплексного теста по математике. Вторая часть этого теста представлена для направления «Математика». Её разбору посвящена настоящая статья.
Разбор вступительного теста в лицей ВШЭ для направления «Математика»
|
Задание 1. При каких |
Разделим «столбиком» многочлен ![]() на квадратный трёхчлен
на квадратный трёхчлен ![]() . В результате получим, что исходный многочлен можно представить в следующем виде:
. В результате получим, что исходный многочлен можно представить в следующем виде:
![]()
![]()
![]()
Остаток от деления ![]() равен нулю тогда и только тогда, когда выполнена следующая система уравнений:
равен нулю тогда и только тогда, когда выполнена следующая система уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases} 13ab+4a+4b = 0 \\ 1-12ab-3a-3b = 0 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b277209be9c57443d71bdb29982d34f7_l3.png)
Для решения этой системы используем замену ![]() и
и ![]() . Тогда получаем следующую систему:
. Тогда получаем следующую систему:
![Rendered by QuickLaTeX.com \[ \begin{cases} 13n+4m = 0 \\ 1-12n-3m = 0 \end{cases}\Leftrightarrow\begin{cases} n = \dfrac{4}{9} \\ m = -\dfrac{13}{9} \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-60149c08f3c6008fc6ae463cd65652cf_l3.png)
Возвращаемся к исходным переменным. Получаем следующую систему:
![Rendered by QuickLaTeX.com \[ \begin{cases} ab = \dfrac{4}{9} \\ a+b = -\dfrac{13}{9} \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f564c904107beff01d950fa578bc8b7e_l3.png)
Решаем эту систему и получаем ответ: ![]() и
и ![]()
|
Задание 2. На графике многочлена с целыми коэффициентами отмечены две точки с целыми координатами. Известно, что расстояние между ними — целое число. Докажите, что соединяющих их отрезок параллелен оси абсцисс. |
Пусть имеем многочлен ![]() с целочисленными коэффициентами. Пусть отмеченные точки имеют целочисленные координаты
с целочисленными коэффициентами. Пусть отмеченные точки имеют целочисленные координаты ![]() и
и ![]() . Требуется доказать, что
. Требуется доказать, что ![]() .
.
Заметим сразу, что разность ![]() представляет собой сумму выражений вида
представляет собой сумму выражений вида ![]() , где все записанные переменные являются целыми числами. Но известна формула:
, где все записанные переменные являются целыми числами. Но известна формула:
![]()
Значит, выражение ![]() делится на
делится на ![]() . То есть
. То есть ![]() тоже делится на
тоже делится на ![]() , и результат этого деления будет являться неким целым числом
, и результат этого деления будет являться неким целым числом ![]() . Получаем, что
. Получаем, что ![]() .
.
Квадрат расстояния между точками ![]() и
и ![]() равен:
равен:
![]()
![]()
Полученный результат должен являться полным квадратом, так как расстояние между отмеченными точками по условию должно быть целым. Но это возможно только при ![]() .
.
Итак, получили, что ![]() , то есть
, то есть ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
|
Задание 3. Два правильных тетраэдра DABC и FABC имеют общее основание ABC и расположены по разные стороны от него. Найдите косинус угла между прямыми AD и BF, если ребро каждого тетраэдра равно 1. |
Изобразим ситуацию на рисунке вместе с некоторыми дополнительными построениями:
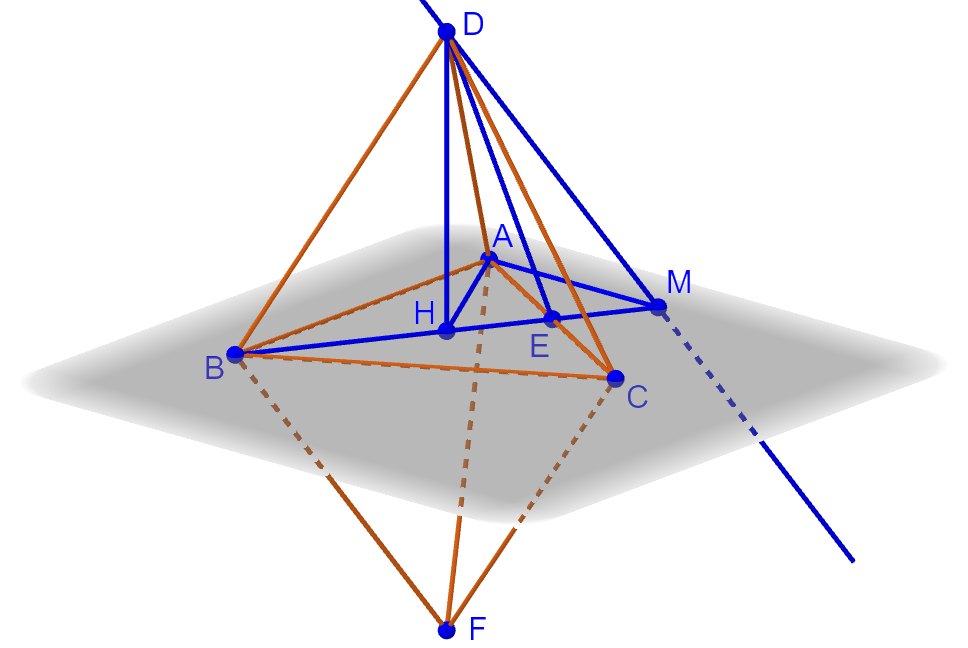
Через точку D провели прямую, которая параллельна прямой BF. Эта прямая пересекла плоскость ABC в точке M. Параллельные прямые BF и DM лежат в одной плоскости BDM. Этой же плоскости принадлежит отрезок DF, который состоит из двух равных отрезков DH и FH, где точка H — геометрический центр треугольника ABC (точка пересечения его биссектрис, медиан и высот). Значит, точка H лежит на прямой, по которой пересекаются плоскости BDM и ABC, то есть на прямой BM. Тогда прямая BM пересекает сторону AC в её середине E (BE — медиана треугольника ABC, так как проходит через точку H).
Ищем ![]() . Это и будет искомый косинус угла между прямым AD и BF, так как по построению прямая BF параллельна прямой DM. Будем искать его из треугольника ADM:
. Это и будет искомый косинус угла между прямым AD и BF, так как по построению прямая BF параллельна прямой DM. Будем искать его из треугольника ADM:
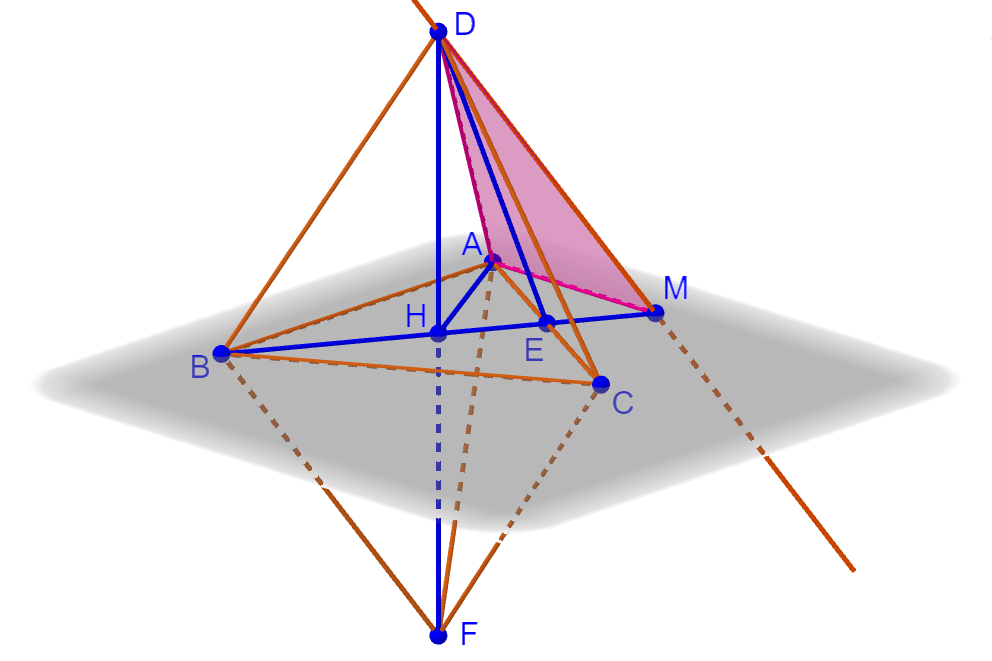
Прямоугольные треугольники BHF и DHM равны по катету и острому углу (DH = HF, так как это высоты одинаковых тетраэдров, и ∠HDM = ∠HFB, так как эти углы являются накрест лежащими при параллельных прямых BF, DM и секущей DF). Поэтому BF = DM = 1. Кроме того, поскольку равны наклонные DM = DA, то равны и проекции AH = HM. Поскольку AH — биссектриса угла A, то ∠HAE = 30°. Так как ∠AEH = 90°, то ∠AHE = 60°. То есть треугольник AHM является равносторонним. Длина его стороны равна AH = BH. Используем, что H — точка пересечения медиан треугольника ABC, поэтому ![]() .
.
Тогда из равнобедренного треугольника ADM по теореме косинусов получаем:
![]()
![]()
Ответ: ![]() .
.
|
Задание 4. Все рёбра правильной треугольной призмы ABCA1B1C1 равны 2. Найдите расстояние между прямыми AB1 и BC1. |
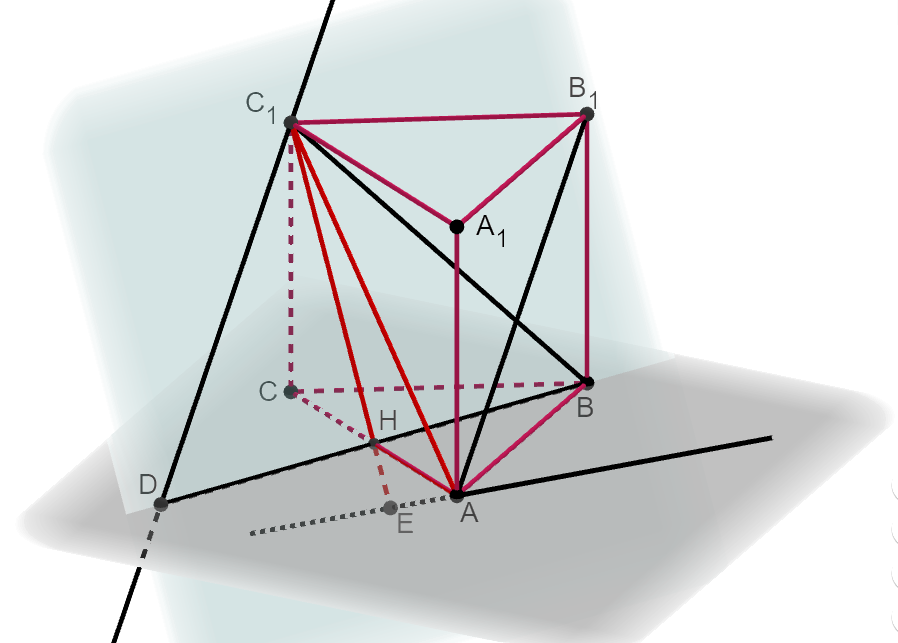
Через точку C1 проведём прямую, параллельную прямой AB1. Она пересечёт плоскость ABC в точке D. Тогда плоскость DC1B параллельна прямой AB1, так как по построению прямая AB1 параллельна прямой DC1, которая лежит в плоскости DC1B. Одна из скрещивающихся прямых, расстояние между которыми нам требуется найти, лежит в плоскости DC1B, а именно прямая BC1, другая параллельна этой плоскости, а именно прямая AB1. Значит, искомое расстояние равно длине перпендикуляра, опущенного из любой точки прямой AB1 на плоскость DC1B. Опустим этот перпендикуляр из точки A. Основанием этого перпендикуляра является точка E. Итак, ищем длину AE:
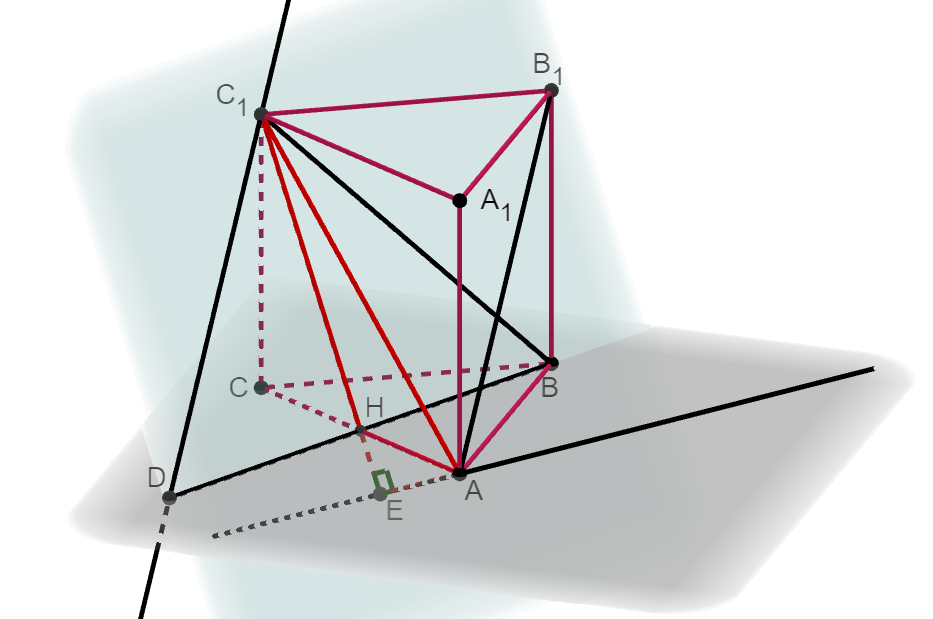
Четырёхугольник DC1B1A является параллелограммом, поэтому и четырёхугольник DCBA тоже является параллелограммом, так как его стороны попарно параллельны. Значит, CH = HA = 1, так как диагонали параллелограмма точкой пересечения делятся пополам. Поэтому из теоремы Пифагора для прямоугольного треугольника C1CH получает, что ![]() . Тогда площадь треугольника C1HA, с одной стороны, равна
. Тогда площадь треугольника C1HA, с одной стороны, равна ![]() , а с другой стороны, она же равна
, а с другой стороны, она же равна ![]() . То есть получаем равенство
. То есть получаем равенство ![]() , откуда находим, что
, откуда находим, что ![]() .
.
Ответ: ![]() .
.
|
Задание 5. В равносторонний треугольник со стороной 1 поместили 30 точек. Докажите, что среди этих точек найдутся хотя бы 4 точки, которые можно накрыть кругом радиуса 1/5. |
Разделим этот треугольник на 9 правильных треугольников со сторонами по ![]() , как показано на рисунке:
, как показано на рисунке:
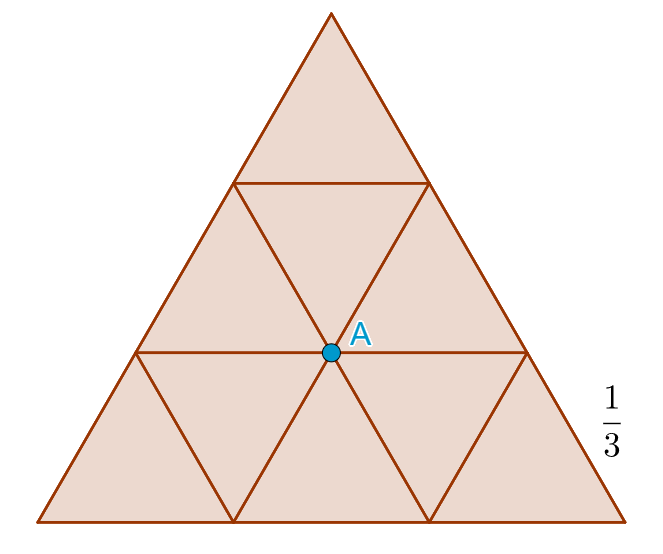
Тогда какому-то треугольнику будет принадлежать не менее четырёх точек. Действительно, если бы в каждом треугольнике находилось по 3 точки или меньше, то всего точек было бы не более ![]() , но по условию их 30. Этому рассуждению не противоречит случай, когда одна из точек совпадает точкой A. Так как всё равно
, но по условию их 30. Этому рассуждению не противоречит случай, когда одна из точек совпадает точкой A. Так как всё равно ![]() . Не возникает проблем и в случае, если какие-то (или даже все) точки окажутся на сторонах маленьких треугольников. В этом случае можно произвольным образом выбрать принадлежность каждой такой «пограничной» точки к какому-то из двух граничащих треугольников. Тогда всё равно найдётся такой треугольник, которому будет принадлежать не менее 4-х точек.
. Не возникает проблем и в случае, если какие-то (или даже все) точки окажутся на сторонах маленьких треугольников. В этом случае можно произвольным образом выбрать принадлежность каждой такой «пограничной» точки к какому-то из двух граничащих треугольников. Тогда всё равно найдётся такой треугольник, которому будет принадлежать не менее 4-х точек.
Радиус описанной около правильного треугольника со стороной ![]() окружности равен
окружности равен ![]() . Значит, такой треугольник можно покрыть кругом радиусом 1/5 вместе со всеми точками 4-мя или более точками, которые ему принадлежат. Что и требовалось доказать.
. Значит, такой треугольник можно покрыть кругом радиусом 1/5 вместе со всеми точками 4-мя или более точками, которые ему принадлежат. Что и требовалось доказать.
|
Задание 6. В группе лицеистов не менее 70% любят уроки английского языка, не менее 75% нравятся уроки физкультуры, не менее 80% любят алгебру и не менее 85% любят уроки математического анализа. Каково наименьшее количество учащихся, которые вообще любят учиться и с радостью посещают уроки английского языка, физкультуры, алгебры и математического анализа? Ответ обосновать. |
Поскольку любителей английского не менее 70%, то не любят английский не более 30% лицеистов. Нам нужно, чтобы их было как можно больше, то есть 30%. Тогда не любят физкультуру 25% лицеистов. Пусть это будут другие люди (не из тех, кто не любит английский), чтобы суммарное количество лицеистов, которые не любят хотя бы один из предметов, было как можно больше. Не любят алгебру 20% учеников. Пусть это тоже будут другие люди. Наконец, не любят математический анализ 15% лицеистов. И это тоже пусть будут какие-то другие люди. Тогда всего получается 30 + 25 + 20 + 15 = 90% лицеистов не любят какой-то один из перечисленных предметов.
Значит, минимальное возможное количество лицеистов, которые любят все четыре предметы равно 10%. Можно привести пример. Если всего лицеистов 20, то распределение может выглядеть следующим образом:
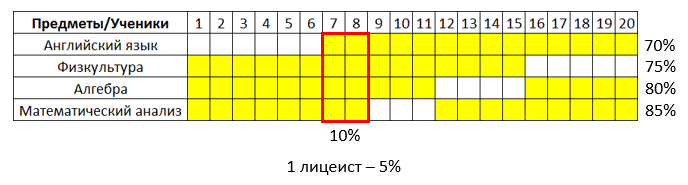
Ответ: 10%.
Подготовка к комплексному тесту по математике в лицей ВШЭ
Для тренировки в решении заданий комплексного теста по математике в лицей ВШЭ вам поможет образовательный портал https://cleverfox.info/. Там выложено большое количество примеров заданий для разных направлений лицея НИУ ВШЭ с подробными решениями от профессионального репетитора.
Ну а также вы можете воспользоваться услугами профессионального репетитора по математике и физике в Москве, который на протяжении многих лет успешно готовит школьников к вступительным испытаниям в лицей ВШЭ, в том числе на направление «Математика». Он поможет вам в сжатые сроки подготовиться к экзамену и избавит вас от лишних переживаний и сложностей, связанных с поступлением в лицей НИУ ВШЭ. Контакты репетитора вы найдёте на этой странице.
Материал подготовил репетитор по математике и физике в Москве Сергей Валерьевич
