В статье представлен разбор заданий второй части ЕГЭ по физике под номерами 25-27. Представлен также видеоурок от репетитора по физике с подробными и понятными пояснениями по каждому из заданий. Если вы только начали свою подготовку к ЕГЭ по физике, эта статья может оказаться для вас очень и очень полезной.
| 25. К потолку лифта с помощью пружины жёсткостью 100 Н/м подвешен груз. Известно, что лифт опускается равноускоренно, причём за 2 с он проходит 5 м пути. Определите массу груза, если удлинение пружины составляет 1,5 см? Ответ дайте в килограммах. |
Начнём с того, что определим ускорение, с которым движется лифт. Он движется из состояния покоя, поэтому справедлива формула: ![]() , где S — пройденный пусть, a — ускорение лифта, t — время движения. Отсюда получаем:
, где S — пройденный пусть, a — ускорение лифта, t — время движения. Отсюда получаем: ![]() м/с2.
м/с2.
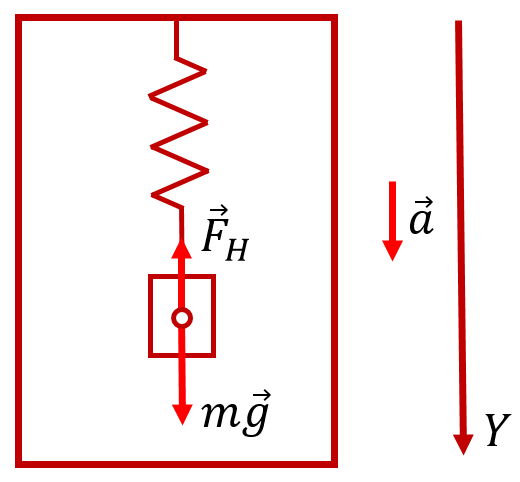
Изобразим силы, действующие на этот груз. Вертикально вниз направлена сила тяжести ![]() , вертикально вверх — сила упругости пружины
, вертикально вверх — сила упругости пружины ![]() (сила Гука), где k — жёсткость пружины, x — удлинение пружины:
(сила Гука), где k — жёсткость пружины, x — удлинение пружины:
После затухания колебаний груза на пружине, вызванных началом движения лифта, груз станет опускаться относительно земли синхронно с лифтом с ускорением ![]() . Для этой ситуации в проекции на вертикальную ось OY, сонаправленную с ускорением, из Второго закона Ньютона получаем:
. Для этой ситуации в проекции на вертикальную ось OY, сонаправленную с ускорением, из Второго закона Ньютона получаем:
![]()
![]()
Расчёты дают ![]() кг.
кг.
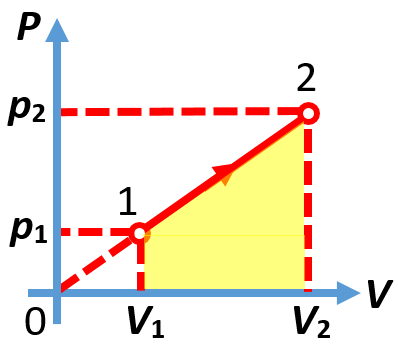
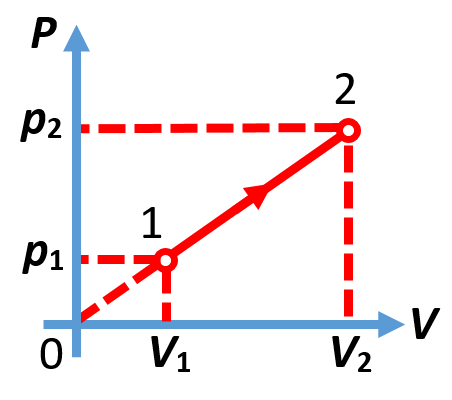 26. 1 моль гелия перешёл из состояния 1 в состояние 2 (см. рисунок). При этом р1 = 100 кПа, V1 = 10 л, V2 = 30 л. Чему равна совершенная газом работа? 26. 1 моль гелия перешёл из состояния 1 в состояние 2 (см. рисунок). При этом р1 = 100 кПа, V1 = 10 л, V2 = 30 л. Чему равна совершенная газом работа? |
Найдём сначала чему равно p2. Для этого используем то, что зависимость p от V в указанном процессе прямо пропорциональная: ![]() , откуда получаем
, откуда получаем ![]() кПа.
кПа.
Из школьного курса термодинамики известно, что работа газа численно равна площади под графиком газового процесса в координатах (p;V). Эта работа положительна, если газ расширялся, и отрицательна в обратном случае. Следовательно, в данном процессе работа газа положительна и численно равна площади трапеции 12V2V1 (на рисунке она выделена жёлтым цветом):
Площадь трапеции равна произведению полусуммы оснований на высоту. То есть получаем в данном случае:
![]()
Расчёты дают значение:
![]() кДж.
кДж.
При вычислениях мы использовали, что 1 л равен 10-3 м3.
| 27. Под воздействием излучения некоторой длины волны из металла выбиваются фотоэлектроны с максимальной кинетической энергией 1,2 эВ. Если вдвое уменьшить длину волны падающего излучения, то эта энергия станет равной 3,95 эВ. Вычислите энергию фотонов в первом случае. |
Энергия фотона связана с длиной волны известным соотношением: ![]() , где h — постоянная Планка, c — скорость света в вакууме, λ — длина световой волны в вакууме. Это означает, что если искомая энергия фотонов в первом случае была равна E, то при уменьшении длины волны падающего излучения вдвое, энергия фотонов станет равной 2E. Запишем уравнения Эйнштейна для фотоэффекта в обоих случаях:
, где h — постоянная Планка, c — скорость света в вакууме, λ — длина световой волны в вакууме. Это означает, что если искомая энергия фотонов в первом случае была равна E, то при уменьшении длины волны падающего излучения вдвое, энергия фотонов станет равной 2E. Запишем уравнения Эйнштейна для фотоэффекта в обоих случаях:
![Rendered by QuickLaTeX.com \[ \begin{cases} E = A+E_{K1} \\ 2E = A+E_{K2}. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-14103d78e1e73069f31a20cf64ed8ce1_l3.png)
Здесь EK1 и EK2 — максимальные кинетические энергии фотоэлектронов в первом и втором случае, соответственно, A — работа выхода электронов из металла. Тогда, вычитая почленно первое уравнение из второго, получаем ![]() эВ.
эВ.
Разбор задач представлен репетитором по физике, Сергеем Валерьевичем
Смотрите также: