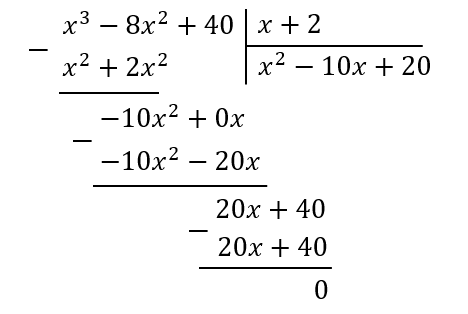В данной статье разобран демонстрационный вариант вступительного комплексного теста по математике для дополнительного набора в 10 класс лицея НИУ ВШЭ в 2018 году. Решения представлены профессиональным репетитором по математике и физике, который специализируется на подготовке школьников к вступительным экзаменам в лицей НИУ ВШЭ. Контакты репетитора вы можете найти на этой странице. Также для подготовки к вступительному тестированию по математике в лицей ВШЭ вы можете воспользоваться сайтом cleverfox.info, где выложены варианты тестов, составленные по мотивам вступительных экзаменов прошлых лет.
В данной статье разобран демонстрационный вариант вступительного комплексного теста по математике для дополнительного набора в 10 класс лицея НИУ ВШЭ в 2018 году. Решения представлены профессиональным репетитором по математике и физике, который специализируется на подготовке школьников к вступительным экзаменам в лицей НИУ ВШЭ. Контакты репетитора вы можете найти на этой странице. Также для подготовки к вступительному тестированию по математике в лицей ВШЭ вы можете воспользоваться сайтом cleverfox.info, где выложены варианты тестов, составленные по мотивам вступительных экзаменов прошлых лет.
Все задания приведены с ответами и подробными решениями от профессионального репетитора. Эти материалы вы сможете использовать для самостоятельной эффективной подготовки.
Дополнительный набор в лицей ВШЭ 2018 — задания по математике первой части теста («Дизайн», «Экмат»)
Рассмотрим сперва решение заданий первой части демонстрационного варианта комплексного теста по математике для дополнительного набора в лицей НИУ ВШЭ 2018 по направлениям «Дизайн» и «Экономика и математика».
|
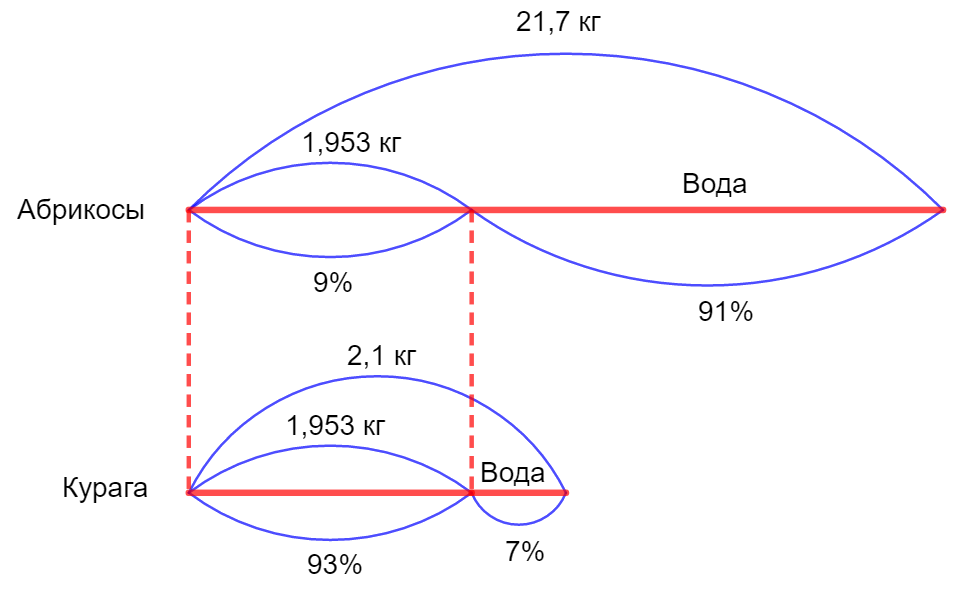
Задание 1. В абрикосах содержится 91 % воды, а в кураге 7% воды. Сколько граммов кураги получится из 21,7 кг абрикосов?
|
Для наглядности изобразим ситуацию на схеме:
Поскольку в абрикосах содержится 91% воды, то остальное содержимое абрикосов составляет 9% от общей массы. При этом общая масса абрикосов (то есть 100%) составляет по условию 21,7 кг. Значит, 1% массы абрикосов составляет 21,7 : 100 = 0,217 кг. Значит, масса остального содержимого абрикосов (кроме воды) составляет 9 × 0,217 = 1,953 кг.
Это же число килограммов составляет 93% содержимого кураги, поскольку остальные 7% составляет вода. Значит, 1% массы кураги составляет 1,953 : 93 = 0,021 кг. Значит, общая масса кураги (то есть 100%) составляет 0,021 × 100 = 2,1 кг = 2100 г.
Правильный ответ: 4
|
Задание 2. В домах, в которых больше пяти этажей, установлен лифт. Выберите утверждения, которые верны при приведённом условии.
|
Из условия следует, что верны только утверждения (2) и (4).
Правильный ответ: 3
|
Задание 3. Цифры
|
Если число делится на 36, то оно делится и на 4, и на 9. Число делится на 4, если последние две его цифры образуют число, которое делится на 4. То есть число ![]() должно делиться на 4. Значит,
должно делиться на 4. Значит, ![]() или
или ![]() . То есть искомое число имеет вид
. То есть искомое число имеет вид ![]() , так как 12 делится на 4, или
, так как 12 делится на 4, или ![]() , так как 16 делится на 4.
, так как 16 делится на 4.
В то же время число делится на 9, если сумма его цифр делится на 9. То есть для числа ![]() получаем, что
получаем, что ![]() , так как
, так как ![]() — делится на 9, а для числа
— делится на 9, а для числа ![]() получаем, что
получаем, что ![]() , так как
, так как ![]() — тоже делится на 9.
— тоже делится на 9.
Для первого числа произведение ![]() , для второго числа это произведение равно
, для второго числа это произведение равно ![]() . Наименьшее решение равно 16.
. Наименьшее решение равно 16.
Правильный ответ: 1
|
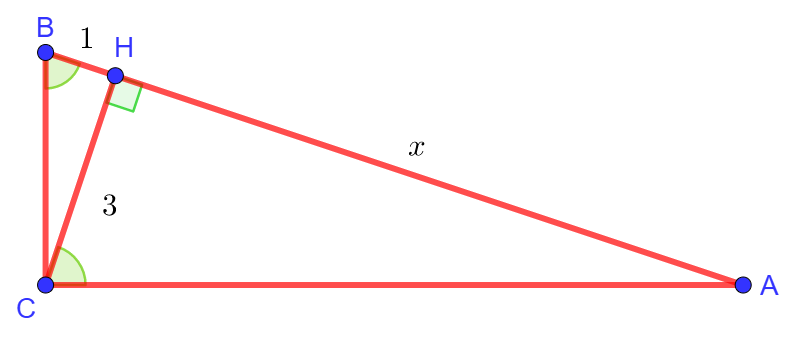
Задание 4. В прямоугольном треугольнике ABC с прямым углом при вершине С высота CH = 3, BH = 1. Найдите площадь треугольника ABC. |
Изобразим сперва ситуацию на рисунке:
Пусть ![]() . Тогда, поскольку треугольник ACB прямоугольный, то
. Тогда, поскольку треугольник ACB прямоугольный, то ![]() . Тогда, поскольку треугольник ACH также прямоугольный, то
. Тогда, поскольку треугольник ACH также прямоугольный, то
![]()
То есть треугольники CBH и ACH подобны по двум углам. Далее пусть ![]() . Тогда из этого подобия получаем, что
. Тогда из этого подобия получаем, что
![]()
То есть ![]() . Тогда искомая площадь треугольника равна
. Тогда искомая площадь треугольника равна ![]() .
.
Правильный ответ: 2
Примечание: подобие треугольников CBH и ACH можно было и не доказывать, сославшись сразу на теорему о пропорциональных отрезках в прямоугольном треугольнике, если вы её хорошо помните.
|
Задание 5. Найдите сумму всех целых
|
Чтобы число ![]() было целым, необходимо, чтобы знаменатель
было целым, необходимо, чтобы знаменатель ![]() был равен -2, -1, 1 или 2. Других делителей у числителя нет. Значит, число
был равен -2, -1, 1 или 2. Других делителей у числителя нет. Значит, число ![]() может принимать одно из четырёх значений: 0, 1, 3, 4. Сумма этих чисел равна 8.
может принимать одно из четырёх значений: 0, 1, 3, 4. Сумма этих чисел равна 8.
Правильный ответ: 2
|
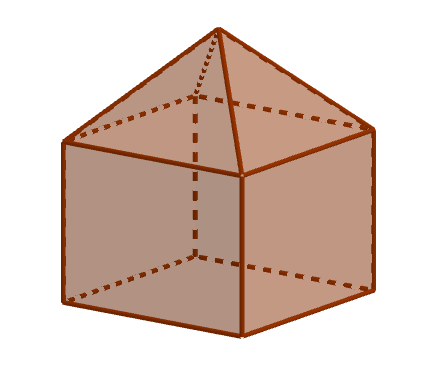
Задание 6. К правильной четырёхугольной пирамиде приклеили прямоугольный параллелепипед так, что их основания совпали. Сколько граней у получившегося многогранника?
|
Для наглядности изобразим ситуацию на рисунке:
Видно, что число граней у получившегося многоугольника равно: ![]() .
.
Правильный ответ: 3
Примечание: в оригинале текст задания звучал следующим образом. «К четырёхугольной пирамиде приклеили параллелепипед так, что их основания совпали. Сколько граней у получившегося многогранника?» То есть не было обозначено, что пирамида является правильной, а параллелепипед прямоугольным. Но в такой формулировке задача не имеет однозначного решения. К примеру, кроме конструкции на предыдущем рисунке, подойдёт ещё и следующая:
В данном случае граней получилось уже 7, а не 9. Но варианты ответов не предполагают того, что ответ может быть многозначным. Таким образом, можно констатировать, что условие составлено авторами некорректно.
|
Задание 7. Решите уравнение |
Выражения, стоящие под знаком модуля обращаются в нуль при ![]() или при
или при ![]() . Отметим эти точки на числовой прямой и найдём знаки выражений
. Отметим эти точки на числовой прямой и найдём знаки выражений ![]() и
и ![]() на каждом из трёх получившихся промежутках:
на каждом из трёх получившихся промежутках:
На каждом из полученных промежутков раскроем теперь оба модуля. При этом в случае, если выражение под знаком модуля принимает отрицательные значения, то модуль должен раскрываться со знаком минус, в противном случае — со знаком плюс:
1) При ![]() получаем уравнение:
получаем уравнение:
![]()
Полученный корень не входит в рассматриваемый промежуток.
2) При ![]() получаем уравнение:
получаем уравнение:
![]()
Полученный корень также не входит в рассматриваемый промежуток.
3) При ![]() получаем уравнение:
получаем уравнение:
![]()
То есть любое значение ![]() из рассматриваемого промежутка является решением исходного уравнения.
из рассматриваемого промежутка является решением исходного уравнения.
Итак, получаем, что ![]() .
.
Правильный ответ: 4
Примечание. На самом деле ответ был понятен сразу, потому что выражение ![]() означает длину отрезка, соединяющего на числовой прямой точки с координатами
означает длину отрезка, соединяющего на числовой прямой точки с координатами ![]() и
и ![]() . Другими словами, если перевести задачу на язык геометрии, то требовалось найти на числовой прямой такую точку, сумма расстояний от которой до точек 1 и -2 будет равна 3. Понятно, что подойдёт любая точка, принадлежащая отрезку от -2 до 1, включая его концы.
. Другими словами, если перевести задачу на язык геометрии, то требовалось найти на числовой прямой такую точку, сумма расстояний от которой до точек 1 и -2 будет равна 3. Понятно, что подойдёт любая точка, принадлежащая отрезку от -2 до 1, включая его концы.
|
Задание 8. Укажите наибольшее решение неравенства
|
Выражение, стоящее под корнем не должно принимать отрицательных значений. Значит, область допустимых значений этого неравенства задаётся следующим условием:
![]()
![]()
![]()
То есть исходное неравенство имеет смысл при ![]() . Значит, если число 4 является решением этого неравенства, то это решение наибольшее. Очевидно, что число 4 является его решением, так как при подстановке этого числа в исходное неравенство, мы получаем верное неравенство
. Значит, если число 4 является решением этого неравенства, то это решение наибольшее. Очевидно, что число 4 является его решением, так как при подстановке этого числа в исходное неравенство, мы получаем верное неравенство ![]() .
.
Правильный ответ: 1
|
Задание 9. Найдите область определения функции |
Как известно, выражение, находящееся под знаком корня, должно быть больше или равно нулю, а выражением, находящееся в знаменателе, не должно обращаться в нуль. Но поскольку ![]() , а
, а ![]() при любом значении
при любом значении ![]() , то область определения функции задаётся следующей системой:
, то область определения функции задаётся следующей системой:
![Rendered by QuickLaTeX.com \[ \begin{cases} 4-x\geqslant 0 \\ (x-3)^2\ne 0 \end{cases} \Leftrightarrow \begin{cases} x\leqslant 4 \\ x\ne 3 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b4d2ca9a7d857d872584bfadccbf2bb3_l3.png)
Итак, система имеет следующее решение: ![]() .
.
Правильный ответ: 4
|
Задание 10. Найдите произведение всех действительных корней уравнения
|
Один из корней легко угадывается: ![]() . Значит, многочлен, стоящий слева от знака равенства, делится на
. Значит, многочлен, стоящий слева от знака равенства, делится на ![]() . Деление «методом уголка» даёт результат:
. Деление «методом уголка» даёт результат:
![]()
Поскольку дискриминант квадратного трёхчлена ![]() отрицателен, то у исходного уравнения есть только один действительный корень:
отрицателен, то у исходного уравнения есть только один действительный корень: ![]() .
.
Правильный ответ: 4
Дополнительный набор в лицей ВШЭ 2018 — задания по математике первой части теста («Психология»)
Разберём теперь решение заданий первой части комплексного теста по математике для дополнительного набора в лицей НИУ ВШЭ 2018 по направлению «Психология».
|
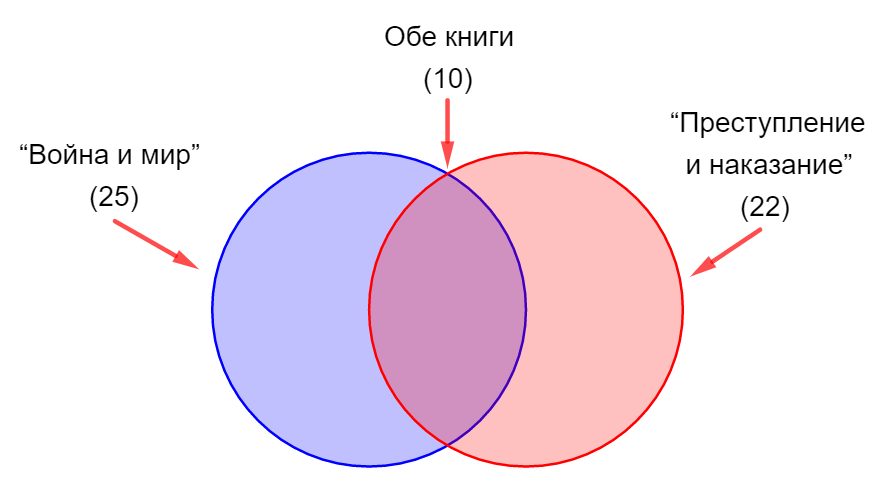
Задание 1. На уроке литературы учитель решил узнать, кто из 40 учеников класса читал книги «Война и мир» и «Преступление и наказание». Результаты опроса оказались таковы: «Войну и мир» читали 25 учащихся, «Преступление и наказание» — 22 учащихся, обе книги читали 10 человек. Сколько человек не прочитали ни одной из этих книг?
|
Пусть синий круг изображает множество из 25 учащихся, которые прочитали «Войну и мир», а красный круг изображает множество из 22 учащихся, которые прочитали «Преступление и наказание». Тогда 10 учащихся, которые прочитали обе книги, будут находиться на пересечении этих множеств:
Посчитаем теперь, сколько учеников в классе прочитали хотя бы одну книгу. Для этого сложим тех, кто прочитал книгу «Война и мир» с теми, кто прочитал книгу «Преступление и наказание». Но тогда мы посчитаем тех, кто прочитал обе книги дважды, поэтому один раз их нужно будет вычесть из общего количества.
Итак, получается, что число учеников, которые читали хотя бы одну из этих книг, равно ![]() . Ну а поскольку всего в классе 40 учеников, то
. Ну а поскольку всего в классе 40 учеников, то ![]() человека не читали ни одной из этих книг.
человека не читали ни одной из этих книг.
Правильный ответ: 3
|
Задание 2. Решите уравнение
|
Поскольку слева выражение стоит под знаком модуля, то уравнение имеет решение только при неотрицательной правой части. То есть имеет место неравенство:
![]()
![]()
![]()
При любом значении ![]() из полученного промежутка выражение, стоящее под знаком модуля, принимает отрицательное или нулевое значение, поэтому модуль раскрывается со знаком минус. Получаем равенство
из полученного промежутка выражение, стоящее под знаком модуля, принимает отрицательное или нулевое значение, поэтому модуль раскрывается со знаком минус. Получаем равенство ![]() , которое верно при любом
, которое верно при любом ![]() . Значит, любое число из отрезка
. Значит, любое число из отрезка ![]() является решением исходного уравнения. Этот отрезок симметричен относительно 0, поэтому сумма всех корней исходного уравнения будет равна 0.
является решением исходного уравнения. Этот отрезок симметричен относительно 0, поэтому сумма всех корней исходного уравнения будет равна 0.
Правильный ответ: 4
| Задание 3. В прямоугольном треугольнике ABC с прямым углом при вершине С высота CH = 3, BH = 1. Найдите площадь треугольника ABC.
|
См. решение задание 4 из предыдущего раздела.
Правильный ответ: 2
|
Задание 4. Решите неравенство
|
Так как ![]() при любых
при любых ![]() , то исходное неравенство можно заменить следующим:
, то исходное неравенство можно заменить следующим: ![]() , то есть
, то есть ![]() . При этом не забываем, что число 2, при котором первая скобка обращается в нуль, также является решением исходного неравенства. Значит, двумя наименьшими целыми решениями данного неравенства являются числа 2 и 4. Их сумма равна 6.
. При этом не забываем, что число 2, при котором первая скобка обращается в нуль, также является решением исходного неравенства. Значит, двумя наименьшими целыми решениями данного неравенства являются числа 2 и 4. Их сумма равна 6.
Правильный ответ: 1
|
Задание 5. Найдите область определения функции В ответе укажите сумму целых отрицательных чисел, принадлежащих области определения функции.
|
Выражение, стоящее в знаменателе не должно быть равно нулю, а выражение, находящееся под корнем, не должно принимать отрицательных значений. Значит, область определения данной функции определяется следующей системой неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} -2x^2-11x+13>0 \\ 9-x^2\ne 0 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8adc93234f64f399f238792aca52fd63_l3.png)
Из второго неравенства получаем, что ![]() .
.
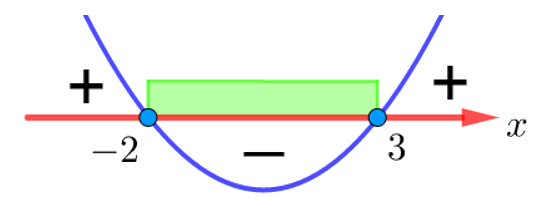
Решаем теперь первое неравенство системы. Отметим на числовой прямой точки, в которых выражение, стоящее слева от знака неравенства, обращается в нуль, и определим знаки этого выражения на полученных промежутках:
Итак, решением первого неравенства системы является промежуток ![]() .
.
Итак, функция определена при ![]() . Сумма целых отрицательных чисел, принадлежащих области определения, равна
. Сумма целых отрицательных чисел, принадлежащих области определения, равна
![]()
Правильный ответ: 3
|
Задание 6. Вычислите |
Выделим в каждом подкоренном выражении полный квадрат. Для первого корня получаем:
![]()
![]()
![]()
Для второго корня получаем:
![]()
![]()
![]()
Тогда после упрощения получаем окончательно:
![]()
Правильный ответ: 3
| Задание 7. Решите иррациональное уравнение
Если корней несколько, в ответе укажите наименьший корень.
|
Уравнение имеет смысл при таких значениях ![]() , при которых оба подкоренных выражения неотрицательны. То есть при
, при которых оба подкоренных выражения неотрицательны. То есть при ![]() .
.
Возведём обе части уравнения в квадрат:
![]()
![]()
Это уравнение имеет решения только при ![]() . В противном случае правая часть отрицательна, а значение корня не может быть отрицательным в действительных числах.
. В противном случае правая часть отрицательна, а значение корня не может быть отрицательным в действительных числах.
Для ![]() ещё раз возведём обе части в квадрат:
ещё раз возведём обе части в квадрат:
![]()
![]()
Корнями последнего уравнения являются числа: ![]() и
и ![]() . Области допустимых значений удовлетворяют оба корня. Но условию, что
. Области допустимых значений удовлетворяют оба корня. Но условию, что ![]() удовлетворяет только первый корень. Значит, это и есть единственный корень исходного уравнения.
удовлетворяет только первый корень. Значит, это и есть единственный корень исходного уравнения.
Правильный ответ: 1
|
Задание 8. Решите неравенство с модулем: В ответе укажите количество целых решений.
|
Преобразуем неравенство к виду:
![]()
1) Для ![]() выражение, стоящее под знаком модуля, принимает отрицательные значения, поэтому модуль раскрывается со знаком минус:
выражение, стоящее под знаком модуля, принимает отрицательные значения, поэтому модуль раскрывается со знаком минус:
![]()
![]()
То есть ![]() .
.
2) Для ![]() выражение, стоящее под знаком модуля, принимает положительные значения, поэтому модуль раскрывается со знаком плюс:
выражение, стоящее под знаком модуля, принимает положительные значения, поэтому модуль раскрывается со знаком плюс:
![]()
![]()
То есть ![]() .
.
Итак, общее решение: ![]() . В это множество входят 4 целых числа: 2, 3, 4 и 5.
. В это множество входят 4 целых числа: 2, 3, 4 и 5.
Правильный ответ: 3
|
Задание 9. Решите уравнение:
|
Один из корней угадывается подбором: ![]() . Значит, выражение стоящее слева делится на
. Значит, выражение стоящее слева делится на ![]() . Делим его методом «уголка»:
. Делим его методом «уголка»:
Значит, исходное уравнение можно заменить следующим:
![]()
Произведение равно нуля, если хотя бы один из множителей равен нулю. Значит либо ![]() , откуда получаем уже угаданный корень
, откуда получаем уже угаданный корень ![]() , либо
, либо ![]() . Последнее квадратичное уравнение решаем с помощью дискриминанта и получаем два оставшихся корня:
. Последнее квадратичное уравнение решаем с помощью дискриминанта и получаем два оставшихся корня: ![]() и
и ![]() . Итак, сумма всех корней уравнения равна:
. Итак, сумма всех корней уравнения равна:
![]()
Правильный ответ: 1
|
Задание 10. Найдите все значения параметра имеет единственное решение. Если значений несколько, в ответе укажите их сумму.
|
Обратим сразу внимание, что при ![]() уравнение не будет иметь решений. Это проверяется прямой подстановкой, в результате которой получается неверное равенство
уравнение не будет иметь решений. Это проверяется прямой подстановкой, в результате которой получается неверное равенство ![]() .
.
При всех остальных ![]() уравнение будет квадратичным. В этом случае, оно будет иметь единственное решение при нулевом дискриминанте:
уравнение будет квадратичным. В этом случае, оно будет иметь единственное решение при нулевом дискриминанте:
![]()
![]()
Получаем ещё два значения: 3 и 4. Но 3, как мы уже выяснили, не подходит. Поэтому остаётся только ![]() .
.
Правильный ответ: 2
Дополнительный набор в лицей ВШЭ 2018 — задания по математике второй части комплексного теста
В данном разделе представлен разбор заданий второй части демонстрационный версии вступительного комплексного теста по математике для дополнительного набора в 10 класс лицея НИУ ВШЭ в 2018 году.
| Задание 1. Решить уравнение в целых числах: |
Перепишем уравнение в виде ![]() . Легко заметить, что пара чисел (1;1) является целочисленным решением этого уравнения. Действительно,
. Легко заметить, что пара чисел (1;1) является целочисленным решением этого уравнения. Действительно, ![]() . То есть получаем, что
. То есть получаем, что
![]()
![]()
![]()
Поскольку мы решаем уравнение в целых числах, то левая часть должна делиться на 3. Но 2 не делится нацело на 3, поэтому на 3 должно делиться выражение, стоящее в скобках. С другой стороны правая часть должна делиться на 2. Но 3 не делится нацело на 2, поэтому на 2 должно делиться выражение, стоящее в скобках. То есть получаем следующую систему:
![Rendered by QuickLaTeX.com \[ \begin{cases} x-1=3k \\ y-1=2k \end{cases} \Leftrightarrow \begin{cases} x = 3k+1 \\ y=2k+1 \end{cases}, k \in Z \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2b4c0b9dbf55858ab66283f86705bb58_l3.png)
То есть в качестве решения исходного уравнения подходит любая целочисленная пара ![]() . Действительно, подставим полученные выражения:
. Действительно, подставим полученные выражения:
![]()
![]()
Ответ: ![]()
| Задание 2. Решите неравенство: |
Неравенство имеет смысл при ![]() или, если умножить обе части на -1,
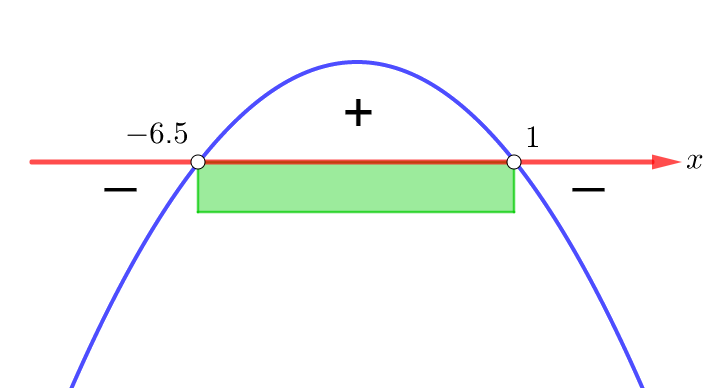
или, если умножить обе части на -1, ![]() . Корни квадратного трёхчлена слева от знака неравенства находим по теореме Виета:
. Корни квадратного трёхчлена слева от знака неравенства находим по теореме Виета: ![]() и
и ![]() . То есть ситуация получается следующая:
. То есть ситуация получается следующая:
Итак, область допустимых значений неравенства задаётся следующим промежутком: ![]() .
.
Перенесём всё в одну сторону и вынесем корень за скобки:
![]()
Последнее неравенство выполняется, когда скобка неотрицательна, то есть при ![]() , или когда корень равен нулю, то есть при
, или когда корень равен нулю, то есть при ![]() и
и ![]() . Тогда с учётом области допустимых значений получаем окончательный ответ:
. Тогда с учётом области допустимых значений получаем окончательный ответ: ![]() .
.
Ответ: ![]()
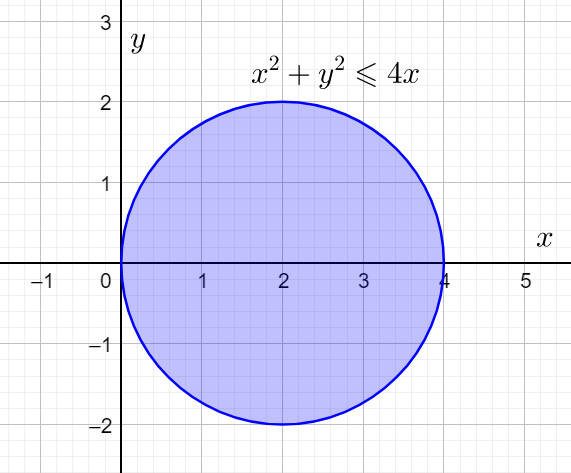
| Задание 3. Изобразить на координатной плоскости множество точек, удовлетворяющих условию: |
Перепишем это неравенство в другом виде:
![]()
![]()
Теперь видно, что искомое множество находится внутри и на границе круга с центром в точке ![]() и радиусом 2:
и радиусом 2:
|
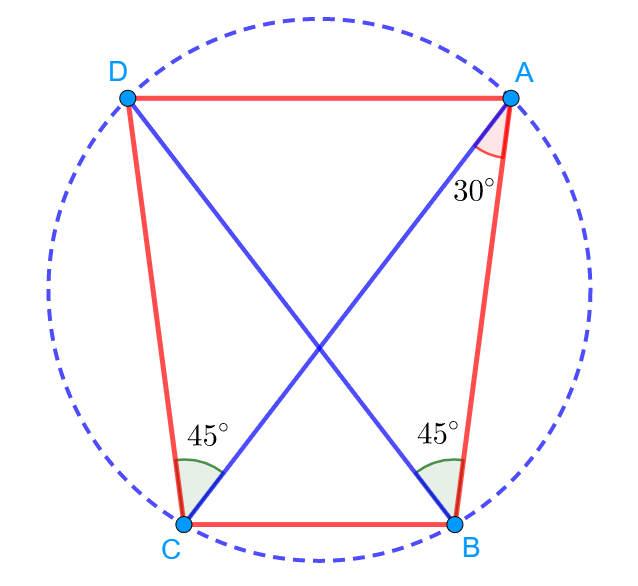
Задание 4. В четырёхугольнике ABCD углы ABD и ACD равны по 45 градусов, а угол BAC равен 30 градусам, BC = 1. А) Докажите, что вокруг четырёхугольника ABCD можно описать окружность Б) Найдите AD. |
Изобразим ситуацию на рисунке:
А) Вокруг четырёхугольника ABCD можно описать окружность, так как сторона AD видно под равными углами из точек B и C. Значит, углы ABD и ACD являются вписанными в окружность, которая проходит через точки A, B, C и D.
Б) Запишем теорему синусов для треугольника CAB:
![]()
Здесь ![]() — радиус описанной окружности. Из последнего равенства получаем, что
— радиус описанной окружности. Из последнего равенства получаем, что ![]() .
.
Теперь запишем теорему синусов для треугольника ADB:
![]()
Из этого равенства получаем, что ![]() .
.
Ответ: ![]()
Примечание: на самом деле четырёхугольник ABCD является равнобедренной трапецией с боковыми сторонами AB и CD, но для решения задачи доказательство этого факта не требуется.
| Задание 5. Найдите все значения параметра |
1) при ![]() , то есть при
, то есть при ![]() требуемое условие выполняется при
требуемое условие выполняется при
![Rendered by QuickLaTeX.com \[ \begin{cases}3a>3 \\ -(2a+1)<1\end{cases}\Leftrightarrow a>1 \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ed6d40c0fb1fe1397134f536f6c69277_l3.png)
То есть в том случае ![]() .
.
2) при ![]() , то есть при
, то есть при ![]() требуемое условие выполняется при
требуемое условие выполняется при
![Rendered by QuickLaTeX.com \[ \begin{cases}3a<1 \\ -(2a+1)>3\end{cases}\Leftrightarrow a<-2 \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e76ab0f9d2d7358cea7d72323cab27d1_l3.png)
То есть в этом случае ![]() .
.
Окончательным ответом служит объединение этих промежутков.
Ответ: ![]()
Подготовка к комплексному тесту для дополнительного набора в лицей НИУ ВШЭ
Если вам требуется подготовка к поступлению в лицей НИУ ВШЭ, то лучшим вариантом являются индивидуальные занятия с профессиональным репетитором, специализирующимся на такой подготовке и имеющим большой опыт. Контакты такого специалиста вы сможете на этой странице. Также вы можете воспользоваться сайтом cleverfox.info, где выложены варианты тренировочных тестов и их подробные решения. Материал постоянно дополняется и обновляется. Эта отличная возможность для самостоятельной подготовки и успешной сдачи вступительного экзамена в лицей НИУ ВШЭ. Успехов в подготовке!
Материал подготовил профессиональный репетитор по математике в Москве Сергей Валерьевич



![Rendered by QuickLaTeX.com \[ y=\sqrt{\dfrac{(4-x)(x^2+1)}{(x-3)^2}} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-722a59ecaf54cd155964527dcb9906ec_l3.png)