В данной статье рассказывается о том, как решать задачи про движение по наклонной плоскости. Рассмотрено подробное решение задачи о движении связанных тел по наклонной плоскости из ЕГЭ по физике.
| Определите ускорение грузов, связанных невесомой и нерастяжимой нитью, перекинутой через невесомый блок, как показано на рисунке, если массы левого и правого груза равны 0.4 и 0.3 кг, соответственно, коэффициент трения левого груза о поверхность наклонной плоскости равен 0.1, а угол наклона наклонной плоскости равен
|
Прежде чем перейти непосредственно к решению задачи, как репетитор по математике и физике, рекомендую тщательно проанализировать ее условие. Начать нужно с изображения сил, которые действуют на связанные тела:
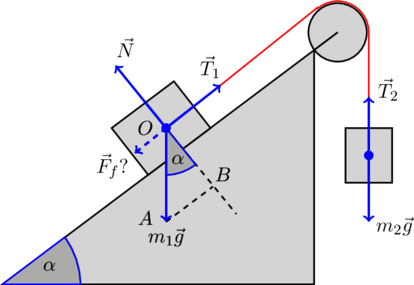
Здесь ![]() и
и ![]() — силы натяжения нити, действующие на левое и правое тело, соответственно,
— силы натяжения нити, действующие на левое и правое тело, соответственно, ![]() — сила реакции опоры, действующая на левое тело,
— сила реакции опоры, действующая на левое тело, ![]() и
и ![]() — силы тяжести, действующие на левое и правое тело, соответственно. С направлением этих сил все понятно. Сила натяжения направлена вдоль нити, сила тяжести вертикально вниз, а сила реакции опоры перпендикулярно наклонной плоскости.
— силы тяжести, действующие на левое и правое тело, соответственно. С направлением этих сил все понятно. Сила натяжения направлена вдоль нити, сила тяжести вертикально вниз, а сила реакции опоры перпендикулярно наклонной плоскости.
А вот с направлением силы трения ![]() придется разбираться отдельно. Поэтому на рисунке она изображена пунктирной линией и подписана со знаком вопроса. Интуитивно понятно, что если правый груз будет «перевешивать» левый, то сила трения будет направлена противоположно вектору
придется разбираться отдельно. Поэтому на рисунке она изображена пунктирной линией и подписана со знаком вопроса. Интуитивно понятно, что если правый груз будет «перевешивать» левый, то сила трения будет направлена противоположно вектору ![]() . Наоборот, если левый груз будет «перевешивать» правый, то сила трения будет сонаправлена с вектором
. Наоборот, если левый груз будет «перевешивать» правый, то сила трения будет сонаправлена с вектором ![]() .
.
Правый груз тянет вниз сила ![]() Н. Здесь мы взяли ускорение свободного падения
Н. Здесь мы взяли ускорение свободного падения ![]() м/с2. Левый груз вниз тоже тянет сила тяжести, но не вся целиком, а только ее «часть», поскольку груз лежит на наклонной плоскости. Эта «часть» равна проекции силы тяжести на наклонную плоскости, то есть катету
м/с2. Левый груз вниз тоже тянет сила тяжести, но не вся целиком, а только ее «часть», поскольку груз лежит на наклонной плоскости. Эта «часть» равна проекции силы тяжести на наклонную плоскости, то есть катету ![]() в прямоугольном треугольнике
в прямоугольном треугольнике ![]() , изображенном на рисунке, то есть равна
, изображенном на рисунке, то есть равна ![]() Н.
Н.
То есть «перевешивает» все-таки правый груз. Следовательно, сила трения ![]() направлена так, как показано на рисунке (мы ее нарисовали от центра масс тела, что возможно в случае, когда тело можно моделировать материальной точкой):
направлена так, как показано на рисунке (мы ее нарисовали от центра масс тела, что возможно в случае, когда тело можно моделировать материальной точкой):
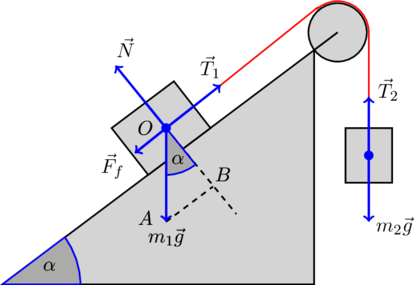
Второй важный вопрос, с которым нужно разобраться, будет ли вообще двигаться эта связанная система? Вдруг окажется так, что сила трения между левым грузом и наклонной плоскостью будет настолько велика, что не даст ему сдвинуться с места?
Такая ситуация будет возможна в том случае, когда максимальная сила трения, модуль которой определяется по формуле ![]() (здесь
(здесь ![]() — коэффициент трения между грузом и наклонной плоскостью,
— коэффициент трения между грузом и наклонной плоскостью, ![]() — сила реакции опоры, действующая на груз со стороны наклонной плоскости), окажется больше той силы, которая старается привести систему с движение. То есть той самой «перевешивающей» силы, которая равна
— сила реакции опоры, действующая на груз со стороны наклонной плоскости), окажется больше той силы, которая старается привести систему с движение. То есть той самой «перевешивающей» силы, которая равна ![]() Н.
Н.
Модуль силы реакции опоры ![]() равен длине катета
равен длине катета ![]() в треугольнике
в треугольнике ![]() по 3-музакону Ньютона (с какой по величине силой груз давит на наклонную плоскость, с такой же по величине силой наклонная плоскость действует на груз). То есть сила реакции опоры равна
по 3-музакону Ньютона (с какой по величине силой груз давит на наклонную плоскость, с такой же по величине силой наклонная плоскость действует на груз). То есть сила реакции опоры равна ![]() Н. Тогда максимальная величина силы трения составляет
Н. Тогда максимальная величина силы трения составляет ![]() Н, что меньше, чем величина «перевешивающей силы».
Н, что меньше, чем величина «перевешивающей силы».
Следовательно, система будет двигаться, причем двигаться с ускорением. Изобразим на рисунке эти ускорения и оси координат, которые нам понадобятся далее при решении задачи:
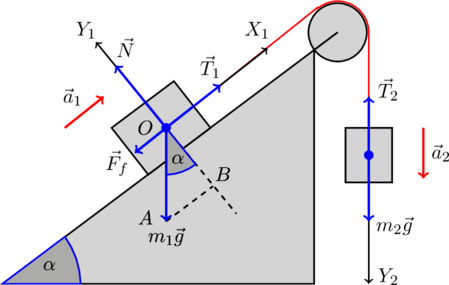
Теперь, после тщательного анализа условия задачи, мы готовы приступить к ее решению.
Запишем 2-ой закон Ньютона для левого тела:
![]()
А в проекции на оси координатной системы ![]() получаем:
получаем:
![]()
Здесь с минусом взяты проекции, векторы которых направлен против направления соответствующей оси координат. С плюсом взяты проекции, векторы которых сонаправлен с соответствующей осью координат.
Еще раз подробно объясним, как находить проекции ![]() и
и ![]() . Для этого рассмотрим прямоугольный треугольник
. Для этого рассмотрим прямоугольный треугольник ![]() , изображенный на рисунке. В этом треугольнике
, изображенный на рисунке. В этом треугольнике ![]() и
и ![]() . Также известно, что в этом прямоугольном треугольнике
. Также известно, что в этом прямоугольном треугольнике ![]() . Тогда
. Тогда ![]() и
и ![]() .
.
Вектор ускорения ![]() целиком лежит на оси
целиком лежит на оси ![]() , поэтому
, поэтому ![]() и
и ![]() . Как мы уже вспоминали выше, по определению модуль силы трения равен произведению коэффициента трения на модуль силы реакции опоры. Следовательно,
. Как мы уже вспоминали выше, по определению модуль силы трения равен произведению коэффициента трения на модуль силы реакции опоры. Следовательно, ![]() . Тогда исходная система уравнений принимает вид:
. Тогда исходная система уравнений принимает вид:
![]()
Запишем теперь 2-ой закон Ньютона для правого тела:
![]()
В проекции на ось ![]() получаем:
получаем:
![]()
Здесь, как и в предыдущем пункте, с минусом взяты проекции, векторы которых противоположно направлены оси ![]() , а с плюсом взяты проекции, векторы которых сонаправлены с осью
, а с плюсом взяты проекции, векторы которых сонаправлены с осью ![]() .
.
В условии сказано, что нить невесомая, то есть не требуется усилий, чтобы привести ее в движение. Следовательно, ![]() . Кроме того, по условию нить нерастяжимая, следовательно левый груз движется синхронно с правым, то есть
. Кроме того, по условию нить нерастяжимая, следовательно левый груз движется синхронно с правым, то есть ![]() .
.
Тогда система уравнений окончательно принимает вид:
![Rendered by QuickLaTeX.com \[ \left\{\begin{array}{lc} T - \mu N - m_1g\sin\alpha = m_1a, & (1)\\ N - m_1g\cos\alpha = 0, & (2)\\ m_2g - T = m_2a. & (3)\\ \end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1038d09dccecc453a537ee1b81812105_l3.png)
Из уравнения (2) выражаем ![]() , из уравнения (3) выражаем
, из уравнения (3) выражаем ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{cases} N = m_1g\cos\alpha, \\ T = m_2g - m_2a. \\ \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7980b38eaeadb050deccf4e779f136c5_l3.png)
Теперь все это подставляем в уравнение (1) и выражаем из него искомое ускорение ![]() :
:
![]()
После подстановки численных значений получаем ![]() м/с2.
м/с2.
Задачи на движением по наклонной плоскости встречаются в той или иной форме практически в каждом варианте ЕГЭ по физике. Научиться их решать должен каждый школьник. Они являются своеобразным индикатором умения ученика использовать законы Ньютона для решения задач по механике. Удачи вам в подготовке к ЕГЭ по физике!
Репетитор по физике на Юго-Западной
Сергей Валерьевич