Данная статья посвящена разбору демонстрационного варианта устной и письменной части вступительного экзамена по математике в 8 класс Московской гимназии № 1543 на Юго-Западе. Сам демовариант находится на официальном сайте гимназии в открытом доступе. Разбор представлен профессиональным репетитором, специализирующимся на подготовке школьников к вступительным экзаменам по математике и физике в гимназию 1543 г. Москвы.
Письменная часть экзамена по математике в гимназию 1543
| 1. Представьте число 3 в виде дроби, у которой числитель есть пятая степень натурального числа, а знаменатель — шестая степень натурального числа. |
Из условия получаем, что ![]() , причём
, причём ![]() . То есть
. То есть ![]() . Берём корень пятой степени из обеих частей:
. Берём корень пятой степени из обеих частей: ![]() . Подбираем
. Подбираем ![]() таким, чтобы результат извлечения корня пятой степени был натуральным. Подойдёт
таким, чтобы результат извлечения корня пятой степени был натуральным. Подойдёт ![]() .
.
Находим теперь значение ![]() :
:
![]()
То есть искомое представление имеет вид:
![]()
| 2. Вычислите:
|
Пусть ![]() . Тогда имеем:
. Тогда имеем:
![]()
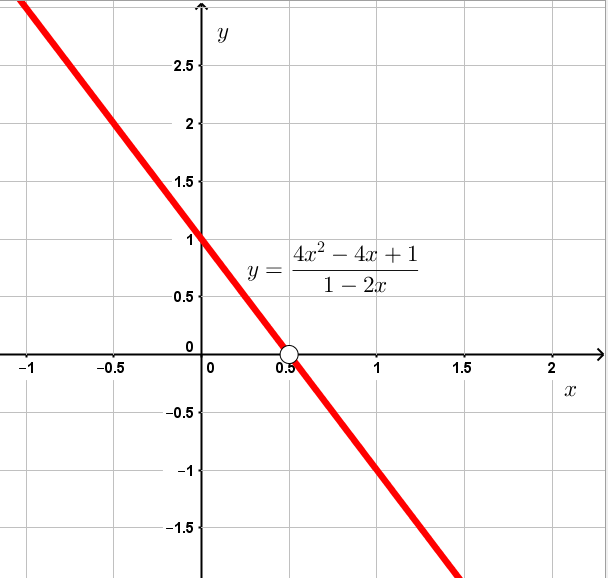
| 3. Постройте график функции
|
Область определения данной функции задаётся неравенством ![]() , поскольку в знаменателе дроби не может быть нуля. То есть
, поскольку в знаменателе дроби не может быть нуля. То есть ![]() , но
, но ![]() :
:
Упростим выражение, стоящее справа:
![]()
То есть график исходной функции — это график линейной функции ![]() , из которой удалена точка с абсциссой
, из которой удалена точка с абсциссой ![]() .
.
| 4. Есть два сплава меди с цинком. В первом отношение массы меди к массе цинка 2:1, во втором — 3:2. Сколько килограммов первого и второго сплава нужно взять, чтобы получить сплав, в котором 17 кг меди и 27 кг цинка? |
Пусть мы взяли ![]() кг первого сплава и
кг первого сплава и ![]() кг второго сплава. Тогда общая масса меди в обоих сплавах равна
кг второго сплава. Тогда общая масса меди в обоих сплавах равна ![]() , и она равна 17 кг. А общая масса цинка в обоих сплавах равна
, и она равна 17 кг. А общая масса цинка в обоих сплавах равна ![]() , и она равна 27 кг. То есть имеет место следующая система уравнений:
, и она равна 27 кг. То есть имеет место следующая система уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases} \frac{2}{3}x+\frac{3}{5}y = 17 \\ \frac{1}{3}x+\frac{2}{5}y = 27. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ef27421b962623abccd444bd160f4ef0_l3.png)
У этой системы нет решений в положительных числах. Ответ к этой системе ![]() . Скорее всего преподаватели гимназии 1543 на Юго-Западе устали проверять вступительные по математике и ошиблись в условии. Подразумеваю, что вместо фразы «сплав, в котором 17 кг меди и 27 кг цинка» имелась ввиду фраза «сплав, в котором 17 кг цинка и 27 кг меди». Если так, то система принимает вид:
. Скорее всего преподаватели гимназии 1543 на Юго-Западе устали проверять вступительные по математике и ошиблись в условии. Подразумеваю, что вместо фразы «сплав, в котором 17 кг меди и 27 кг цинка» имелась ввиду фраза «сплав, в котором 17 кг цинка и 27 кг меди». Если так, то система принимает вид:
![Rendered by QuickLaTeX.com \[ \begin{cases} \frac{2}{3}x+\frac{3}{5}y = 27 \\ \frac{1}{3}x+\frac{2}{5}y = 17. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-eb4a53f4f04ee293c18f7b0440ac4edc_l3.png)
Умножаем обе части второго уравнения на 2 и вычитаем почленно из второго уравнения первое. В результате получаем следующее уравнение: ![]() , откуда получаем
, откуда получаем ![]() кг. Подставляем это значение в первое уравнение и получаем
кг. Подставляем это значение в первое уравнение и получаем ![]() , откуда
, откуда ![]() кг. То есть нужно взять 9 кг первого сплава и 35 кг второго.
кг. То есть нужно взять 9 кг первого сплава и 35 кг второго.
| 5. Внутри треугольника ABC, у которого |
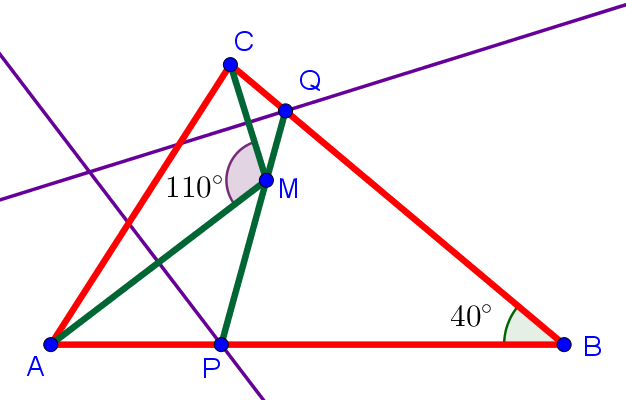
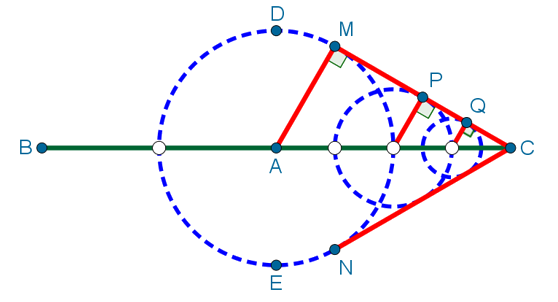
Изобразим ситуацию на рисунке:
Фиолетовыми линиями на рисунке обозначены срединные перпендикуляры. Все точки срединного перпендикуляра к отрезку равноудалены от концов этого отрезка. Значит, CQ = QM и AP = PM. То есть треугольники CQM и APM — равнобедренные. Углы при их основаниях равны. То есть
(1) ![]()
Рассмотрим треугольник AMC. В этом треугольнике ∠AMC=110°. Значит, сумма оставшихся двух углов равна 70°, так как сумма углов в треугольнике равен 180°. То есть ∠CAM+∠ACM = 70°.
С другой стороны в треугольнике ABC ∠B=40°. Значит, по той же причине два оставшихся угла в сумме дают 140°. То есть ∠PAC+∠ACB = 140°. Вычитаем почленно из последнего уравнения предпоследнее и получаем:
![]()
Глядя на рисунок, получаем ∠PAM+∠MCQ=70°. С учётом равенств (1), получаем ∠CMQ+∠AMP=70°. То есть ∠CMQ+∠AMP+∠AMC=180°. То есть ∠PMQ — развёрнутый, то есть точки P, Q и M лежат на одной прямой. Что и требовалось доказать.
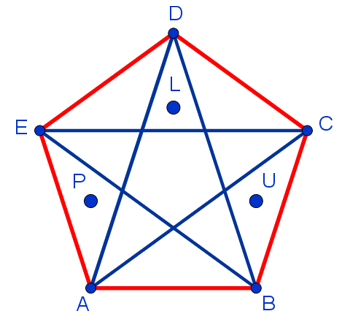
| 6. Какое минимальное количество точек надо поставить внутри выпуклого пятиугольника, чтобы внутри любого треугольника, вершинами которого являются вершины пятиугольника, оказалась по крайней мере одна точка? |
Можно убедиться, что одной или двух точек не достаточно. Ни одна конфигурация в этом случае не подойдёт. А вот трёх точек уже достаточно. И расположить их внутри пятиугольника нужно следующим образом:
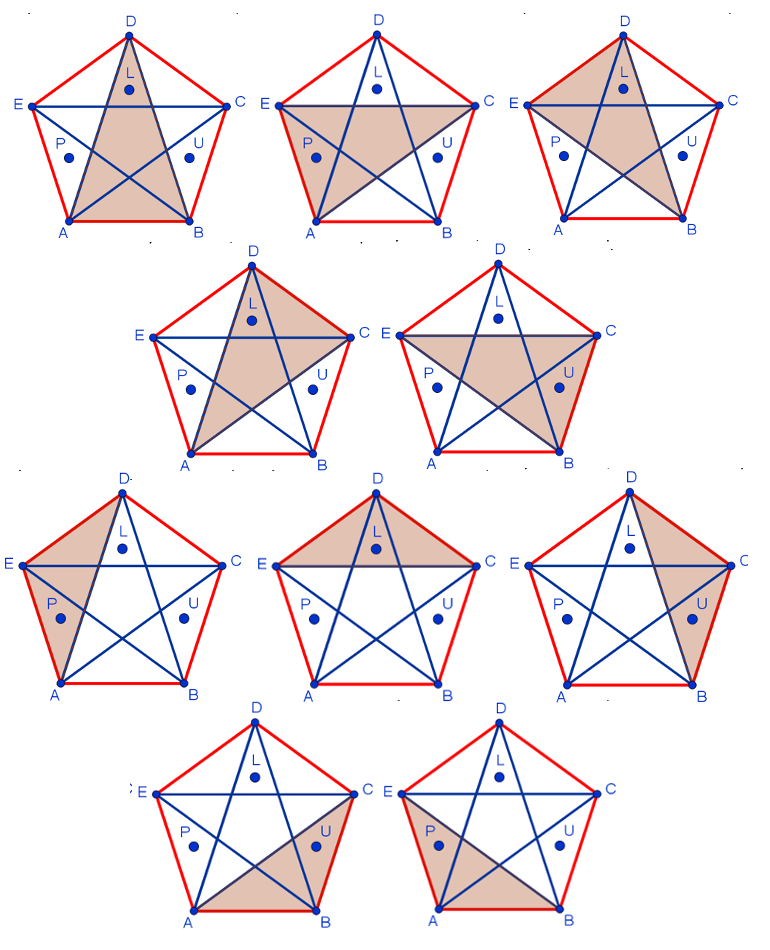
Действительно, в этом случае внутри любого треугольника, вершинами которого являются вершины пятиугольника, оказывается одна точка:
Итак, правильный ответ к этой задаче: 3.
Примечание. Понятно, что рисовать все эти конструкции на экзамене не нужно. Здесь они приведены исключительно из соображений наглядности.
Устная часть вступительного по математике в 8 класс Московской гимназии № 1543 на Юго-Западе
| 1. Можно ли поставить вместо звёздочек в выражении |
Да, можно. Например, так:
![]()
![]()
| 2. В таблице размером |
Пусть ![]() — число столбцов в таблице. Поскольку сумма чисел в каждом столбца равна 10, то сумма всех чисел во всех столбцах равна
— число столбцов в таблице. Поскольку сумма чисел в каждом столбца равна 10, то сумма всех чисел во всех столбцах равна ![]() . Аналогично, пусть
. Аналогично, пусть ![]() — число строк в таблице. Поскольку сумма чисел в каждой строке равна 10, то сумма всех чисел во всех строках равна
— число строк в таблице. Поскольку сумма чисел в каждой строке равна 10, то сумма всех чисел во всех строках равна ![]() . Но сумма чисел во всех строках равна сумме чисел во всех столбцах, поскольку это одни и те же числа. То есть
. Но сумма чисел во всех строках равна сумме чисел во всех столбцах, поскольку это одни и те же числа. То есть ![]() , то есть
, то есть ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
| 3. Из трёхзначного числа вычли сумму кубов его цифр. Какое наибольшее число могло при этом получиться? |
Пусть само число имеет вид ![]() , где
, где ![]() ,
, ![]() и
и ![]() — цифры этого числа, причём
— цифры этого числа, причём ![]() . Тогда само число равно
. Тогда само число равно ![]() , а его разность с суммой кубов его цифр равна:
, а его разность с суммой кубов его цифр равна:
![]()
![]()
Простым перебором убеждаемся, что первое слагаемое даёт максимальный вклад в общую сумму при ![]() , второе — при
, второе — при ![]() , третье — при
, третье — при ![]() или
или ![]() . То есть искомое число — это либо 621, либо 620. И в том, и в другом случае максимальная разность между самим числом и сумой кубов его чисел равна 396.
. То есть искомое число — это либо 621, либо 620. И в том, и в другом случае максимальная разность между самим числом и сумой кубов его чисел равна 396.
| 4. Белка собрала 10 орехов массой 100 г. Ни один орех не весит более 12 г. Всегда ли белка сможет раздать орехи двум своим бельчатам так, чтобы никто из них не обиделся. (Бельчонок обижается, если он получил а) хотя бы на 10 г меньше; б) более, чем на 10 г меньше, чем брат). |
Нет, сможет не всегда. Предположим, что белка собрала 9 орехов массой по 11,1 г и 1 орех массой 0,1 г. Если их разделить между бельчатами, то у какого-то бельчонка окажется орех массой 0,1 г, а все остальные массой по 11,1 г, а у второго все орехи будут массой по 11,1 г. При попытке разделить их так, чтобы разница между общей массой орехов у каждого из бельчат была наименьшей, у первого бельчонка будет 4 ореха по 11,1 г и 1 орех массой 0,1 г (общая масса 44,5 г), а у второго — 5 орехов по 11,1 г (общая масса 55.5 г). Разница между массами орехов у бельчат составит 11 г. Значит, первый бельчонок обидится, как в случае а), так и в случае б).
| 5. Илья стоит на автотрассе Москва — Владимир, а мимо него проезжают машины: «МАЗ» (во Владимир), «Ауди» (в Москву) и «Камаз» (во Владимир). В тот момент, когда мимо Ильи проехал «МАЗ», «Ауди» и «Камаз» были от него на равных расстояниях. Когда мимо Ильи проехал «Ауди», «МАЗ» и «Камаз» были от него на равных расстояниях. Илья полагает, что когда мимо него проедет «Камаз», «МАЗ» и «Ауди» будут от него также на равных расстояниях. Прав ли он? |
Пусть скорость машины «Ауди» составляет ![]() , скорость машины «МАЗ» составляет
, скорость машины «МАЗ» составляет ![]() , скорость машины «Камаз» также составляет
, скорость машины «Камаз» также составляет ![]() .
.
Рассмотрим сначала случай, когда сперва мимо Ильи проезжает «МАЗ». Пусть в этот момент расстояния от Ильи до машин «Ауди» и «Камаз» равны по ![]() . Тогда машина «Ауди» проедем мимо Ильи через
. Тогда машина «Ауди» проедем мимо Ильи через ![]() . При этом машина «Камаз» в этот момент окажется от Ильи на расстоянии
. При этом машина «Камаз» в этот момент окажется от Ильи на расстоянии
![]()
Одновременно машина «МАЗ» отъедет от Ильи на расстояние то же (по условию) расстояние ![]() . Значит имеет место равенство:
. Значит имеет место равенство:
![]()
После того, как мимо Ильи проедет «Ауди» должно пройти ещё ![]() времени, чтобы «Камаз» подъехал к Илье. Тогда расстояние от Ильи до «Ауди» станет равно
времени, чтобы «Камаз» подъехал к Илье. Тогда расстояние от Ильи до «Ауди» станет равно ![]() . А расстояние от Ильи до «МАЗа» станет равно:
. А расстояние от Ильи до «МАЗа» станет равно:
![]()
![]()
Значит ![]() . То есть в данном случае Илья прав. Второй случай, когда сперва мимо Ильи проезжает «Ауди», доказывается абсолютно аналогично. Ответ: Илья прав.
. То есть в данном случае Илья прав. Второй случай, когда сперва мимо Ильи проезжает «Ауди», доказывается абсолютно аналогично. Ответ: Илья прав.
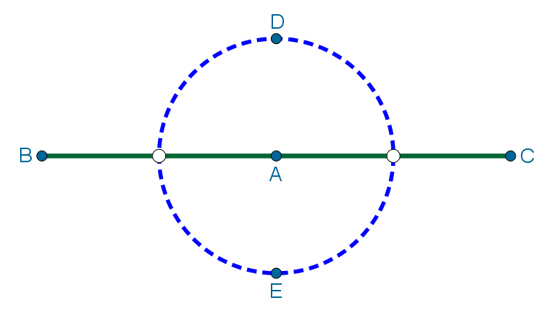
| 6. Петя стоит на прямолинейной дороге, проходящей по полю. Скорость движения Пети по полю 3 км/ч, а по дороге — 6 км/ч. Отметьте на рисунке те точки, куда Петя может дойти не более, чем за час. |
Допустим, что в начальный момент Петя находится в точке A на прямолинейной дороге. Тогда он может пройти по дороге 6 км вправо или влево до точек A и B:
Он также может пойти из точки A по полю. Тогда после 1 ч движения он окажется в любой точке поля внутри круга радиусом 3 км. На рисунку DE — диаметр этого круга:
У Пети, однако, остаётся также вариант пройти сперва некоторое расстояние по дороге, а затем начать двигаться по полю. Например, если он пройдёт полчаса по дороге по направлению к точке C (см. рисунок выше), то он окажется ровно на середине отрезка AC. И у него остается ещё полчаса, чтобы добраться на любой точки на поле внутри круга радиусом ![]() км:
км:
Обратим внимание, что радиус круга получился вдвое меньше расстояния от центра этого круга до точки C. Фокус в том, что это соотношение остаётся постоянным для любой точка на дороге. Действительно, пусть Петя двигался до какой-то точки на дороге время ![]() ч, тогда оставшееся время движения составляет
ч, тогда оставшееся время движения составляет ![]() ч. За это время Петя может продолжить своё движение по дороге и пройти
ч. За это время Петя может продолжить своё движение по дороге и пройти ![]() ч либо пойти по полю и оказаться в любой его точке внутри круга радиусом
ч либо пойти по полю и оказаться в любой его точке внутри круга радиусом ![]() км, что вдвое меньше.
км, что вдвое меньше.
Сказанное означает, что если провести касательные к каждой изображённой окружности из точки C, то все радиусы этих окружностей, проведённые в точки касания, будут перпендикулярны касательным и будут вдвое меньше расстояний от центров этих окружностей до точки C. То есть каждая касательная будет наклонена под углом ![]() к дороге и проходить через одну точку C. То есть на самом деле все эти касательные будут совпадать. Ко всем окружностям будет одна общая касательная:
к дороге и проходить через одну точку C. То есть на самом деле все эти касательные будут совпадать. Ко всем окружностям будет одна общая касательная:
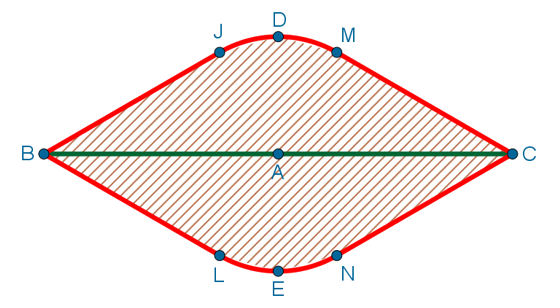
Понятно, что абсолютно симметричная ситуация получилась бы, если бы Петя пошёл влево от точки A. То есть область, которая содержит все точки, куда Петя сможет дойти не более, чем за час, выглядит следующим образом:
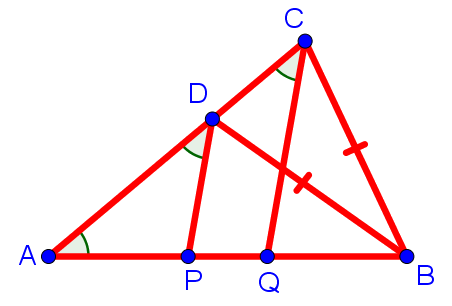
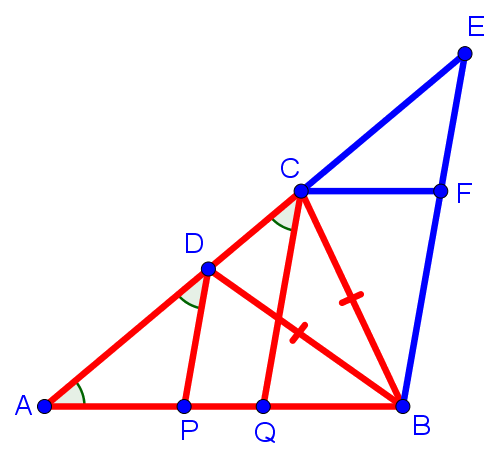
| 7. В треугольнике ABC на стороне AC выбрана точка D так, что BC = BD. На стороне AB выбраны точки P и Q так, что ∠PDA = ∠QCA = ∠BAC. Докажите, что AP = BQ. |
На рисунке ситуация выглядит следующим образом:
Отметим сразу, что прямые PD и QC параллельны, поскольку равны соответственные углы ADP и ACQ при секущей DC. Кроме того, треугольники ADP и ACQ — равнобедренные с основаниями AD и AC, соответственно.
Выполним следующее дополнительное построение. Во-первых, проведём через точку B прямую, параллельную прямым DP и QC, затем продлим сторону AC до пересечения с этой прямой в точке E. Во-вторых, через точку C проведём прямую, параллельную стороне AB до пересечения с прямой BE в точке F. В результате получим следующий рисунок:
∠ADP = ∠ACQ = ∠AEB, так как эти углы соответственные при параллельных прямых DP, CQ и EB. То есть ∠EAB = ∠AEB. Значит, треугольник ABE — равнобедренный, и AB = BE,
Треугольник DBC — равнобедренный. Значит углы при его основании равны. То есть угол ∠BDC = ∠DCB. Значит, ∠ADB = ∠BCE, так как они смежные с ∠BDC и ∠DCB, соответственно.
Значит, два угла треугольника ADB соответственно равны двум углам треугольника BCE, поэтому равны и третьи углы. То есть ∠ABD = ∠EBC.
То есть равны треугольники ADB и CBE по двум сторонам и углу между ними (AB = BE, BD = BC и ∠ABD = ∠CBE). Значит, AD = CE.
Из этого следует, что по стороне и двум прилежащим к ней углам равны треугольники ADP и CFE (∠DAP = ∠ECF, ∠ADP = ∠CEF и AD = CE). Значит, AP = PD = CF = EF. Нам важно, что AP = CF.
По построению QCFB — параллелограмм. Значит, CF = QB, так как у параллелограмма противоположные стороны равны. Значит, AP = CF = QB. То есть AP = QB. Что и требовалось доказать.
| 8. В воскресенье каждый из учеников класса один раз побывал на катке. Известно, что каждый мальчик встретил там всех своих одноклассниц. Докажите, что либо все мальчики, либо все девочки из этого класса в какой-то момент были на катке одновременно. |
Если найдутся какие-то два мальчика, которые не встретились друг с другом, то каждый из них должен был находиться на катке в тот момент, когда там были все девочки. Иначе эти мальчики встретились бы не со всеми девочками, что противоречит условию. Аналогично, если найдутся какие-то две девочки, которые не встретились друг с другом, то каждая из них должна была находиться на катке в тот момент, когда там были все мальчики. Иначе эти девочки встретились бы не со всеми мальчиками, что также противоречит условию. Значит был такой момент, когда либо все мальчики, либо все девочки были на катке одновременно. Что и требовалось доказать.
Вот такие задачи предлагаются для решения на вступительном экзамене по математике в 8 класс Московской гимназии №1543 на Юго-Западе. Если вам требуется помощь в подготовке к вступительным экзаменам по математике или физике в гимназию 1543, рекомендуем вам обратиться к профессиональному репетитору Сергею Валерьевичу, занимающемуся подготовкой школьников к этим экзаменам. Всю необходимую информацию о репетиторе и его занятиях вы сможете найти на этой странице. Успехов вам в подготовке и удачи на экзаменах!