В задании 23 из второй части диагностической работы для 9 класса по математике, прошедшей в московских школах 19 декабря 2011, была предложена геометрическая задача. Для ее решения от учеников требовалось знание так называемой теоремы о секущей и касательной, о существовании которой многие девятиклассники, как оказалось, и не подозревали. Выявив сей пробел, постараемся тут же его закрыть.
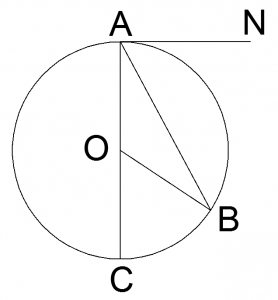
Лемма о вневписанном угле: величина угла, образованного касательной и хордой, имеющими общую точку на окружности, равна половине угловой величины дуги, заключенной между его сторонами.
Например, на рисунке ∠BAN = 1/2 AB. Докажем это. Проведем диаметр АС. Касательная перпендикулярна диаметру, проведенному в точке касания, следовательно, ∠CAN = 90°. Известно, что вписанный угол равен половине центрального угла дуги, на которую он опирается. Тогда ∠BAC = ∠BOC/2, ∠NAB = 90° — ∠BAC, значит ∠NAB = 90° — ∠BOC/2 = (180° — ∠BOC)/2 = ∠АОВ/2, то есть равен половине угловой величины дуги ВА.
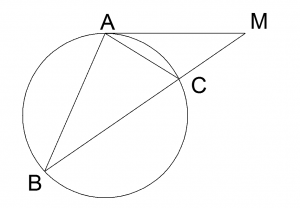
Теорема о секущей и касательной: если из внешней точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.
Например, на рисунке МА2 = МВ · МС. Доказать это несложно. Действительно, вневписанный угол CAM равен вписанному углу ABC, поскольку оба опираются на одну дугу. Тогда треугольники АМС и ВМА подобны по двум углам (∠CAM = ∠ABC, ∠M — общий). Из подобия следует, что MC : MA = МА : MB, откуда получаем, что МА2 = МВ · МС.
На этом теоретическая часть закончена, перейдем к практике. Разберем одно из заданий диагностической работы по математике для 9 класса, прошедшей в Москве 19 декабря 2011 года.
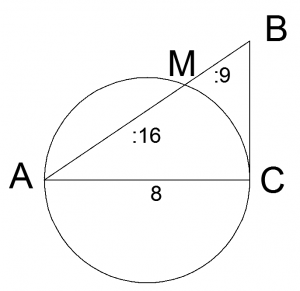
Пример. Длина катета AC прямоугольного треугольника ABC равна 8 см. Окружность с диаметром AC пересекает гипотенузу AB в точке M. Найдите площадь треугольника ABC, если известно, что AM : MB = 16 : 9.
Решение:
Пусть BC = y см, AM = 16x см и MB = 9x см. Поэтому гипотенуза AB = 25x см.
По теореме Пифагора: y2 = 625x2 — 64.
По теореме о секущей и касательной: y2=25x · 9x = 225x2.
Следовательно, 225x2 = 625x2 — 64, откуда x2 = 4/25.
Тогда y2 = 225 · 4/25; y = 15 · 2/5 = 6.
Следовательно, искомая площадь треугольника равна:
1/2 · AC · BC = 1/2 · 8 · 6 = 24 см2.
Ответ: 24 см2.
Материал подготовил репетитор по математике в Москве в районе станции метро «Тёплый Стан», Сергей Валерьевич

1/2 · AC · BC = 1/2 · 8 · 6 = 24 см2. — неправильно!!! должно быть : 1/2 · AВ · МC = 1/2 · 10 · 24/5 = 24 см2. Сергей, Вам пара за такое решение!
Ну можно и через высоту MC площадь искать, согласен. Мне важно было теорему о секущей и касательной в решении использовать, поэтому я другой способ выбрал. Не пойму только, почему Вы считаете его неправильным.
теорему Вы использовали составив второе уравнение, но площадь треугольника считается через высоту или полу периметр!!! Так в школе учат. Если Вы вывели такое равенство и соотношение в прямоугольном треугольнике — это хорошо, но не все школьники это поймут. Решение надо все таки писать более понятно, здесь не олимпиада.
Тут собственно площадь через высоту и основание и находится, только они с катетами совпадают, что для прямоугольного треугольника естественно. И в школе обычно обращается внимание, на то, что площадь именно прямоугольного треугольника можно найти как полупроизведение катетов, так что в таком виде решение должно быть понятно школьнику. Ваше решение требует еще дополнительного доказательства, что CM является высотой, повторение чего впрочем также иной раз может оказаться для ученика не лишним:-).
а вообще-то , спасибо за подсказку
Ребята, это частный случай ромбоида
С этим я, пожалуй, позволю себе не согласиться:-)
Все 23 задачи в ГИА нерешаемы….((((
мы же не все вундеркинды
Ну может быть и не обязательно их решать. Если решить все задачи кроме 23, результат все равно будет блестящий. Хотя учиться их решать, конечно, нужно. На ЕГЭ они тоже будут всех ждать:-)