 В этой статье вы найдёте решение заданий из варианта вступительного экзамена по математике в лицей 1535. Оригинал варианта размещён на официальном сайте учебного заведения. Там же вывешены на всеобщее обозрение всяческие награды лицея, а также его текущие и зачастую очень высокие позиции в различных рейтингах.
В этой статье вы найдёте решение заданий из варианта вступительного экзамена по математике в лицей 1535. Оригинал варианта размещён на официальном сайте учебного заведения. Там же вывешены на всеобщее обозрение всяческие награды лицея, а также его текущие и зачастую очень высокие позиции в различных рейтингах.
Лицей No 1535 — достаточно сильное учебное заведение, поэтому конкурс при поступлении высок. Меня, как репетитора по математике и физике, часто просят помочь подготовиться к вступительным экзаменам в этот лицей. Я с радостью этим занимаюсь, поскольку это является частью моей специализации. Предлагаю вам самим оценить сложность экзаменационных заданий. Возможно, вам тоже не помешает помощь профессионального репетитора, чтобы за короткий срок привести знания в систему и приобрести необходимые навыки для решения подобных заданий.
Решение заданий первой части вступительного экзамена по математике в лицей 1535
| Задание 1. Вычислить:
|
Выполняем необходимые действия в соответствующем порядке:
![]()
![]()
| Задание 2. Найдите разность наибольшего и наименьшего корней уравнения |
Перед нами стандартное квадратное уравнение. Причём ![]() ,
, ![]() , c=
, c=![]() . Вычисляем дискриминант:
. Вычисляем дискриминант:
![]()
Дискриминант положителен, поэтому корней у данного квадратного (или квадратичного) уравнения будет два. Вычисляются они по следующим формулам:
![Rendered by QuickLaTeX.com \[ x_{1,2}=\frac{-b\pm\sqrt{D}}{2a} = \left[\begin{array}{l} x_1 = 1 \\ x_2 = -\frac{23}{5}. \end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-63cefb71d6f506479234ef61c71f1faa_l3.png)
Искомая разность наибольшего и наименьшего корней равна ![]() .
.
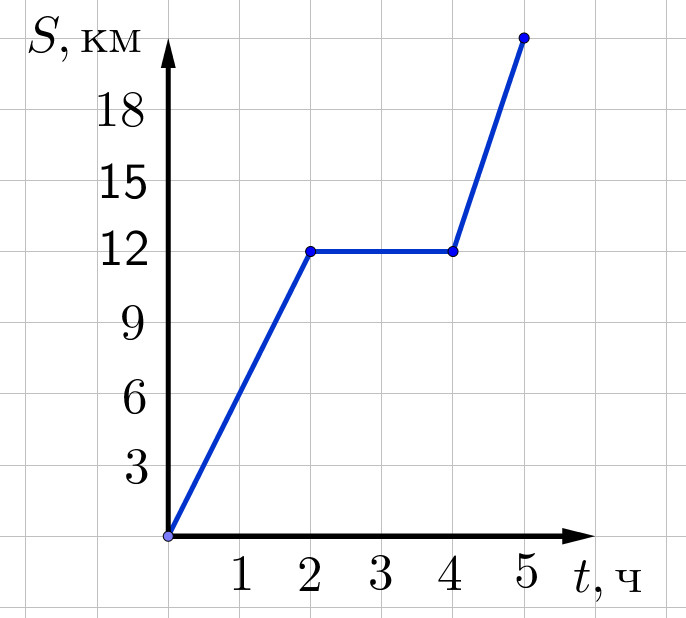
| Задание 3. На рисунке представлен график движения катера по озеру от посёлка до города с остановкой в сосновом бору. Чему была равна скорость катера (в км/ч) при движении от соснового бора до города? |
Как видно из графика, стоянка катера в сосновом бору закончилась через 4 часа после отбытия из посёлка. Далее катер за 1 ч проплыл расстояние 9 км, то есть двигался со скоростью 9 км/ч.
| Задание 4. Найдите значение выражения
|
Воспользуемся известными формулами «Квадрат разности» и «Разность квадратов»:
![]()
| Задание 5. Решите уравнение |
После элементарного упрощения левой части уравнения (приведения подобных слагаемых, вынесения общего множителя ![]() в скобках и деления правой и левой частей уравнения на
в скобках и деления правой и левой частей уравнения на ![]() ) мы получаем следующее уравнение:
) мы получаем следующее уравнение: ![]() . Как хорошо известно, произведение равно нулю, только и только тогда, когда хотя бы один из множителей равен нулю. То есть либо
. Как хорошо известно, произведение равно нулю, только и только тогда, когда хотя бы один из множителей равен нулю. То есть либо ![]() , либо
, либо ![]() . Откуда получаем
. Откуда получаем ![]() и
и ![]() . По условию требуется найти среднее арифметическое корней уравнения. Тогда ответ будет:
. По условию требуется найти среднее арифметическое корней уравнения. Тогда ответ будет:
![]()
Важное примечание! В тексте вступительного испытания по математике в лицей 1535, размещённого на сайте, ответом к этому заданию является чисто 4. Я полагаю, что связано это с тем, что уважаемые преподаватели устали проверять экзаменационные работы абитуриентов и ошиблись в записи условия. Скорее всего, имелось ввиду уравнение ![]() . Тогда корня будет три: 0, -5 и 17, и среднее арифметическое равно 4.
. Тогда корня будет три: 0, -5 и 17, и среднее арифметическое равно 4.
Но и это ещё не всё. На самом деле составители варианта ошиблись в этом задании дважды. Они просят найти среднее арифметическое корней. То есть просят сложить все корни и поделить полученное число на количество корней. Но ![]() в этом задании — это корень двойной кратности! И если на сумму корней это не влияет, числитель остаётся тем же, то знаменатель должен быть увеличен на 1. И ответ, строго говоря, должен быть другим. Но это пусть останется на совести составителей.
в этом задании — это корень двойной кратности! И если на сумму корней это не влияет, числитель остаётся тем же, то знаменатель должен быть увеличен на 1. И ответ, строго говоря, должен быть другим. Но это пусть останется на совести составителей.
| Задание 6. Наименьшим целым решением неравенства
является число … |
Умножим обе части неравенства на ![]() . Знак неравенства при этом не меняется, потому что умножение происходит на положительное число. В результате получаем:
. Знак неравенства при этом не меняется, потому что умножение происходит на положительное число. В результате получаем:
![]()
Раскрываем скобки, переносим члены, содержащие неизвестную переменную ![]() в правую сторону неравенства, остальные члены — в левую. Не забываем при этом, что при переносе из одной части неравенства в другую меняется знак того, что мы переносим. В результате приходим к следующему неравенству:
в правую сторону неравенства, остальные члены — в левую. Не забываем при этом, что при переносе из одной части неравенства в другую меняется знак того, что мы переносим. В результате приходим к следующему неравенству:
![]()
То есть ответ: ![]() .
.
| Задание 7. Сократить дробь |
Как вы понимаете, число 1535 здесь выбрано не случайно. Задание решается с использованием стандартных формул сокращенного умножения, а именно формулы «Разность квадратов». Перед её использованием вынесем минус из знаменателя и запишем его перед дробью. В результате получаем следующее выражение:
![]()
Значение этого выражения при ![]() равно -1539.
равно -1539.
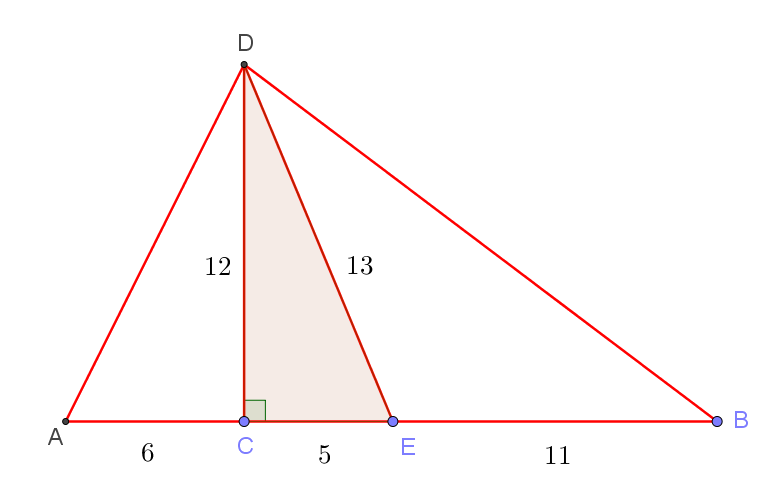
| Задание 8. К основанию треугольника длиной 22 проведены высота и медиана, длины которых равны соответственно 12 и 13. Чему равна длина наибольшей боковой стороны этого треугольника? |
Большая часть решения изображена на рисунке снизу:
Из прямоугольного треугольника CDE по теореме Пифагора находим, что длина CE равна 5. Это говорит о том, что высота DC лежит внутри треугольника ABD. Тогда длина CB равна 16. Далее уже из прямоугольного треугольника CDB по теореме Пифагора находим искомую большую боковую сторону DB, длина которой составляет 20.
| Задание 9. Найдите значение параметра |
Используем теорему Виета. В результате получаем вот такую систему уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases} 3x_1+5x_2=2 \\ x_1+x_2=4 \\ x_1x_2 = q. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8448ecd73158b76299f98bec42e72cb6_l3.png)
Из первых двух уравнений получаем ![]() и
и ![]() . Тогда искомое значение параметра равно
. Тогда искомое значение параметра равно ![]() .
.
| Задание 10. У двух преподавателей, работающих вместе с одинаковой производительностью, ушло 7,5 часов на проверку экзаменационных работ. Сколько времени (в часах) уйдёт на проверку экзаменационных работ, если производительность одного из преподавателей упадёт на 50%? |
Эта задача, по-видимому, является намёком абитуриентам, насколько тяжёлым трудом является проверка преподавателями их работ. Ну что ж, пожалеем бедных преподавателей и решим эту несложную задачку.
Пусть общая работа равна 1, а начальная производительность каждого преподавателя равна ![]() относительных единиц. Поскольку, работая вместе с одинаковой производительностью, преподаватели выполняют работу за 7,5 часов, то имеет место уравнение
относительных единиц. Поскольку, работая вместе с одинаковой производительностью, преподаватели выполняют работу за 7,5 часов, то имеет место уравнение ![]() . Если какой-то преподаватель снизит свою производительность на 50%, то она станет равной
. Если какой-то преподаватель снизит свою производительность на 50%, то она станет равной ![]() . Тогда общая производительность станет равной
. Тогда общая производительность станет равной ![]() . То есть всю работу преподаватели выполнят за 10 часов.
. То есть всю работу преподаватели выполнят за 10 часов.
Решение заданий второй части вступительного экзамена по математике в лицей 1535
| Задание 11.
а) Упростите выражение: б) Приведите пример значения переменной |
Идём по порядку. Выполняем задание под буквой а). Требуется упростить выражение. Для этого сперва преобразуем выражение, которое находится в скобках:
![]()
![]()
![]()
Теперь «по старшинству» операций следует очередь деления:
![]()
![Rendered by QuickLaTeX.com \[ \frac{2a}{(a-3)^2(3+a)}\cdot\frac{(a-3)^2}{1} = \frac{2a}{3+a}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f29cd586eee05e98bdf77a4ff831894e_l3.png)
Осталось только сложить две дроби:
![]()
б) Само собой разумеется, все преобразования в предыдущем пункте были выполнены в области допустимых значений исходного выражения. А определить эту область можно было уже на этапе разложения на множители всех знаменателей. Ведь каждому известно, что знаменатель не должен быть равен нулю. Поэтому область допустимых значений исходного выражения включает все числа, кроме ![]() и
и ![]() . Эти же значения можно привести в качестве примера в этом пункте.
. Эти же значения можно привести в качестве примера в этом пункте.
| Задание 12. Грузовик двигался по грунтовой дороге с некоторой постоянной скоростью. Из-за плохого качества дороги он отстал от графика на 6 минут. Выехав на асфальтированную дорогу, грузовик увеличил скорость на 4 км/ч, после чего, проехав 36 километров, он ликвидировал отставание по графику. Чему была равна первоначальная скорость грузовика? |
Решаем эту задачу. По-видимому, имеется ввиду, что грузовик задержался на 6 минут из-за того, что ехал по плохой дороге с меньшей, чем планировалось скоростью. Пусть эта скорость равна ![]() км/ч. Затем его скорость увеличилась на 4 км/ч, то есть стала равна
км/ч. Затем его скорость увеличилась на 4 км/ч, то есть стала равна ![]() км/ч. На участке дороги протяжённостью 36 км он ликвидировал опоздание на 6 минут, то есть на
км/ч. На участке дороги протяжённостью 36 км он ликвидировал опоздание на 6 минут, то есть на ![]() ч. Этот участок он проехал за
ч. Этот участок он проехал за ![]() ч. Если бы он двигался с прежней скоростью, то проехал бы это расстояние за
ч. Если бы он двигался с прежней скоростью, то проехал бы это расстояние за ![]() . То есть имеет место уравнение:
. То есть имеет место уравнение:
![]()
В области допустимых значений это уравнение эквивалентно следующему:
![]()
Нам, конечно же, подходит только положительный ответ 36 км/ч.
| Задание 13.
а) Постройте на одном координатном поле графики функций б) С помощью построенных графиков указать множество всех решений системы в) С помощью построенных графиков указать множество всех решений неравенства г) Найти все значения параметра |
Как видите, данное задание предполагает графическое решение. Выполним его по пунктам.
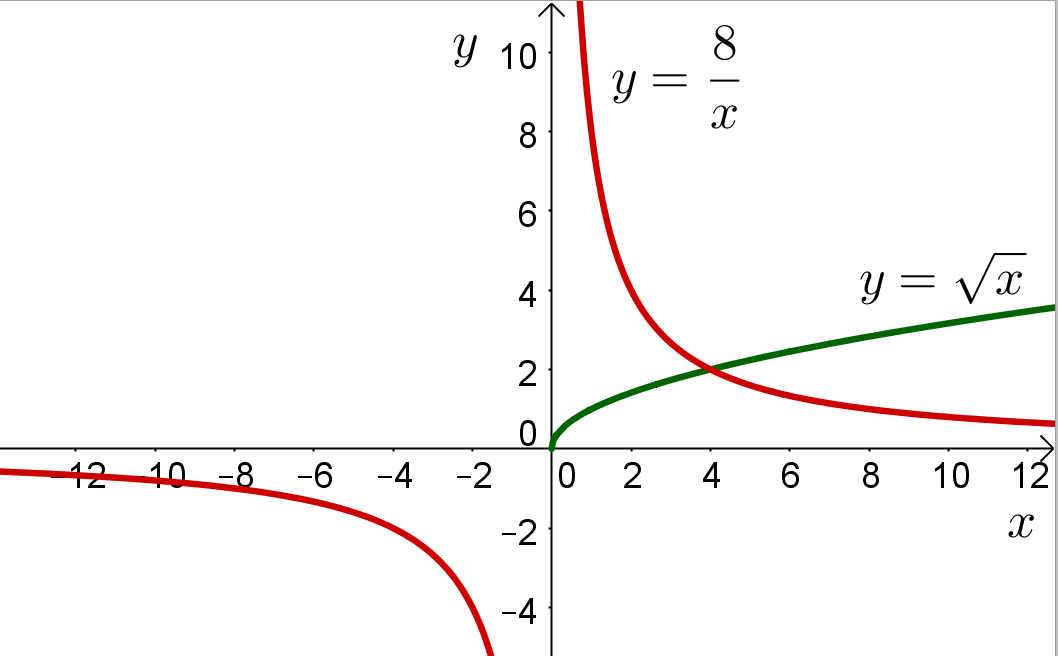
а) Строим графики функций в одной системе координат:
б) Пары координат всех точек пересечения изображённых графиков будут составлять множество всех решений указанной системы. Видно, что такая пара одна. Это точка ![]() .
.
в) Для ответа на вопрос задачи под буквой в) нужно найти абсциссы всех точек, для которых график функции ![]() лежит ниже графика функции
лежит ниже графика функции ![]() . Видно, что искомое множество задаётся промежутком
. Видно, что искомое множество задаётся промежутком ![]() .
.
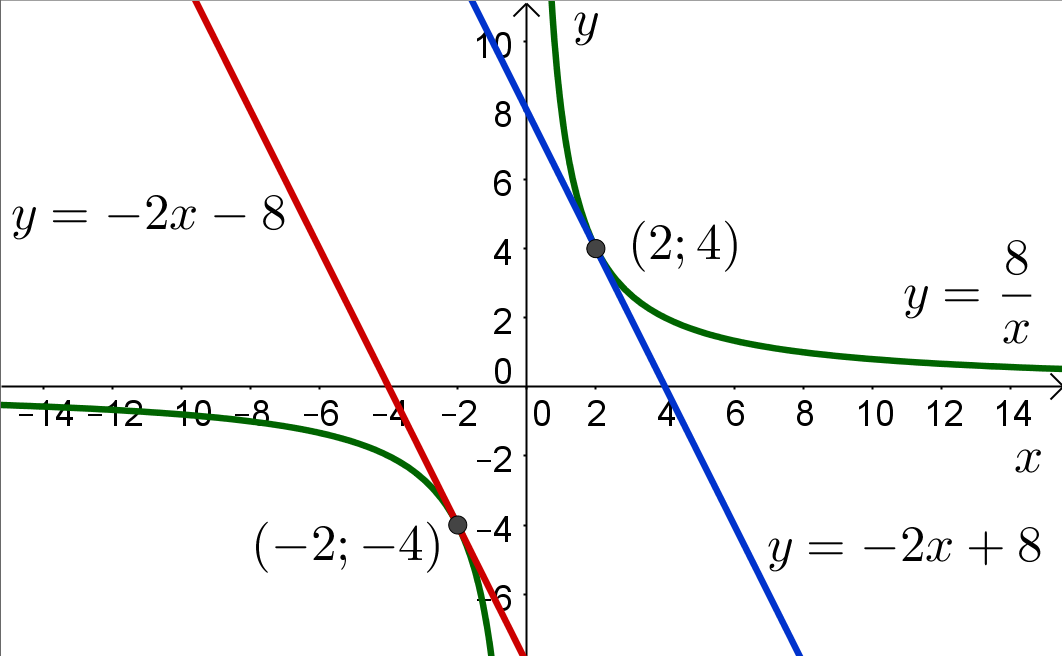
г) график функции ![]() представляет собой прямую, которая перемещается вверх или вниз в зависимости от значения параметра
представляет собой прямую, которая перемещается вверх или вниз в зависимости от значения параметра ![]() . Эта прямая будет иметь единственную точку пересечения (точнее — точку касания) с графиком функции
. Эта прямая будет иметь единственную точку пересечения (точнее — точку касания) с графиком функции ![]() при
при ![]() . Данная ситуация изображена на рисунке снизу.
. Данная ситуация изображена на рисунке снизу.
Разбор заданий вступительного экзамена в лицей 1535 представлен репетитором по математике и физике, Сергеем Валерьевичем

![Rendered by QuickLaTeX.com \[ \begin{cases} y=\sqrt{x} \\ y=\frac{8}{x} \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-19cb1b52f0732e1232b6949b21b4dd95_l3.png)