Физико-математический лицей «Вторая школа» — это достаточно сильное образовательное учреждение г. Москвы. Поток желающих обучаться в этом лицее традиционно очень высок. Но поступить в него удаётся далеко не каждому абитуриенту, поскольку для этого требуется сдать вступительные экзамены. На сайте учебного заведения приведены примеры заданий вступительного экзамена по математике для 10 класса (устной и письменной части). В данной статье предлагаю вашему вниманию разбор предложенных заданий. Оцените их сложность, чтобы узнать, насколько вы готовы к сдаче вступительного экзамена в Московскую физико-математическую школу №2 (Государственный лицей «Вторая школа»).
Физико-математический лицей «Вторая школа» — это достаточно сильное образовательное учреждение г. Москвы. Поток желающих обучаться в этом лицее традиционно очень высок. Но поступить в него удаётся далеко не каждому абитуриенту, поскольку для этого требуется сдать вступительные экзамены. На сайте учебного заведения приведены примеры заданий вступительного экзамена по математике для 10 класса (устной и письменной части). В данной статье предлагаю вашему вниманию разбор предложенных заданий. Оцените их сложность, чтобы узнать, насколько вы готовы к сдаче вступительного экзамена в Московскую физико-математическую школу №2 (Государственный лицей «Вторая школа»).
Задания письменной части вступительного экзамена в лицей «Вторая школа»
| 1. Упростите выражение:
|
Введём замену ![]() и представим выражение в виде:
и представим выражение в виде:
![Rendered by QuickLaTeX.com \[ \left(\frac{x}{x-2}+\frac{x^2-4x+2}{(x-2)(x-1)}\right)\cdot\frac{(1-x)(1+x)}{2(1-2x)}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-6ff66852946f872a71329ea8a5814b71_l3.png)
Далее, используя стандартные правила преобразования выражений, получаем:
![]()
Итак, окончательный ответ: ![]() .
.
| 2. Решите неравенство:
|
a) Заметим сразу, что для ![]() неравенство не выполняется.
неравенство не выполняется.
б) Для ![]() оно равносильно следующему:
оно равносильно следующему:
![]()
![]()
То есть с учётом условия ![]() в данном случае получаем:
в данном случае получаем: ![]() .
.
в) Для ![]() неравенство равносильно следующему:
неравенство равносильно следующему:
![]()
![]()
То есть с учётом условия ![]() получаем в этом случае:
получаем в этом случае: ![]() .
.
Итак, окончательно получаем: ![]() .
.
| 3. Решить уравнение:
|
Область допустимых решений уравнения составляют все действительные числа, кроме тех, что удовлетворяют уравнению:
![]()
В области допустимых значений данное уравнение равносильно следующему:
![]()
а) Для ![]() получаем:
получаем:
![]()
Оба значения входят в указанный промежуток. Однако, корень ![]() не входит в область допустимых значений исходного уравнения.
не входит в область допустимых значений исходного уравнения.
б) Для ![]() получаем:
получаем:
![]()
У последнего уравнения решений нет, поскольку его дискриминант отрицателен.
Итак, ![]() .
.
| 4. Решить графически систему уравнений:
|
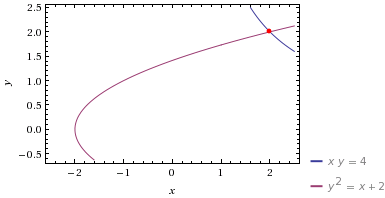
Геометрическим местом точек, удовлетворяющих условию ![]() , является гипербола. Геометрическим местом точек, удовлетворяющих условию
, является гипербола. Геометрическим местом точек, удовлетворяющих условию ![]() , — парабола с вершиной в точке
, — парабола с вершиной в точке ![]() и ветвями, направленными вправо. Изобразим их на одном координатном поле:
и ветвями, направленными вправо. Изобразим их на одном координатном поле:
Видно, что решением предложенной системы уравнений является пара ![]() .
.
| 5. Найдите |
а) Упростим первое выражение, воспользовавшись формулой преобразования произведения косинусов в сумму:
![]()
![]()
б) Второе выражение преобразуем, используя формулы приведения и понижения степени:
![]()
в) Итак, окончательно получаем: ![]() .
.
| 6. В геометрической прогрессии первый, третий и пятый члены равны соответственно первому, четвёртому и шестнадцатому члену некоторой арифметической прогрессии. Найти пятый член арифметической прогрессии, если первый её член равен 5. |
Пусть разность арифметической прогрессии равна ![]() , а знаменатель геометрической прогрессии равен
, а знаменатель геометрической прогрессии равен ![]() . Тогда первый, третий и пятый члены геометрической прогрессии, а также первый, четвёртый и шестнадцатый члены арифметической прогрессии будут равны соответственно:
. Тогда первый, третий и пятый члены геометрической прогрессии, а также первый, четвёртый и шестнадцатый члены арифметической прогрессии будут равны соответственно:
![]()
Тогда имеет место следующая система уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases} 5q^2 = 5+3d \\ 5q^4 = 5+15 d \end{cases}\Rightarrow q^4-5q^2+4=0\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-bd026744961966d337f51da415e68b14_l3.png)
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{l} \begin{cases} d = 0 \\ q^2 = 1 \end{cases}\\ \begin{cases} d = 5 \\ q^2 = 4 \end{cases} \end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8a248c3938a500cf4ed7535d645ecbe8_l3.png)
В первом тривиальном случае пятый член арифметической прогрессии равен её первому члену, то есть 5. Во втором случае пятый член арифметической прогрессии равен 25.
| 7. Из точки C окружности проведены две хорды CA и CB так, что |
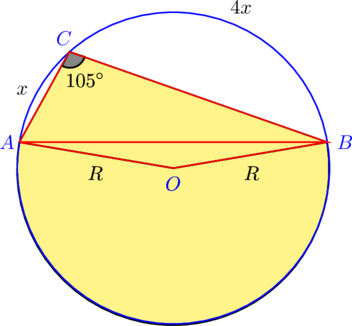
Искомая фигура состоит из трёх частей: треугольника ABC, треугольника ABO и сектора с вершиной O и дугой AB, не содержащей точки C. Найдём последовательно площади всех трёх фигур и сложим их, чтобы получить ответ.
а) Ищем площадь сектора. Вписанный угол ACB опирается на дугу AB, не содержащую точку C, градусная мера которой равна, соответственно, ![]() . Центральный угол AOB, опирающийся на эту дугу также равен
. Центральный угол AOB, опирающийся на эту дугу также равен ![]() . Тогда искомая площадь сектора равна:
. Тогда искомая площадь сектора равна:
![]()
б) Ищем площадь треугольника AOB. Меньший угол AOB равен ![]() . Треугольник равнобедренный с боковым сторонами, которые равны радиусу окружности. Следовательно, его площадь равна:
. Треугольник равнобедренный с боковым сторонами, которые равны радиусу окружности. Следовательно, его площадь равна:
![]()
в) Ищем площадь треугольника ACB. По условию дуга CB, не содержащая точки A, в четыре раза длиннее, чем дуга AC, не содержащая точки B. Градусная мера полной окружности равна ![]() . Поэтому имеет место уравнение:
. Поэтому имеет место уравнение:
![]()
Отсюда градусные меры малых дуг AC, CB и AB равны ![]() ,
, ![]() и
и ![]() соответственно.
соответственно.
Ищем неизвестные углы треугольника ABC. Вписанный угол CAB опирается на дугу BC и равен половине её градусной меры, то есть ![]() . Аналогично, угол CBA равен
. Аналогично, угол CBA равен ![]() .
.
Сторону AB находим из треугольника AOB по теореме косинусов:
![]()
С помощью формулы понижения степени можно показать также, что:
![]()
Тогда из теоремы синусов для треугольника ABC получаем:
![]()
В последнем преобразовании воспользовались формулой приведения:
![]()
То есть получаем:
![Rendered by QuickLaTeX.com \[ AC = R\sqrt{2+\sqrt{3}}\cdot\frac{\sqrt{2-\sqrt{3}}}{\sqrt{2+\sqrt{3}}} = = R\sqrt{2-\sqrt{3}}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-d13cac18d59b334b817d5125fdf2d1ce_l3.png)
То есть площадь треугольника ABC равна:
![]()
![]()
Тогда искомая площадь равна:
![]()
Примечание. Есть способ чуть более короткий и изящный, основанный на использовании формулы площади треугольника через радиус описанной окружности: ![]() . Однако, здесь я сознательно его не использовал, поскольку далеко не все школьные учителя знакомят учеников на своих уроках с этой формулой.
. Однако, здесь я сознательно его не использовал, поскольку далеко не все школьные учителя знакомят учеников на своих уроках с этой формулой.
Решение некоторых заданий устной части вступительного экзамена в лицей «Вторая школа»
| 1. Какое из чисел больше: |
Из школьного курса математики известно, что ![]() . Поэтому сравним сперва
. Поэтому сравним сперва ![]() и
и ![]() .
.
Возводим обе части в квадрат и получаем: ![]() и
и ![]() . Сравниваем тогда
. Сравниваем тогда ![]() и
и ![]() .
.
Вновь возводим обе части в квадрат и получаем: ![]() и
и ![]() . То есть
. То есть ![]() , а значит и
, а значит и ![]() .
.
| 2. Найдите последнюю цифру числа: |
Ищем закономерность:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т. д.
и т. д.
Закономерность такова: идут группы по 4 числа, в конце которых в указанном порядке стоят цифры: ![]() ,
, ![]() ,
, ![]() и
и ![]() . Замечаем, что
. Замечаем, что ![]() .
.
Следовательно, будет ![]() таких групп чисел. Поэтому последняя цифра последнего числа будет равна
таких групп чисел. Поэтому последняя цифра последнего числа будет равна ![]() .
.
| 3. Доказать, что для всех чётных натуральных чисел n число |
Поскольку n — четное натуральное число, его можно представить в виде ![]() , где k — натуральное число. Тогда представленное выражение принимает вид:
, где k — натуральное число. Тогда представленное выражение принимает вид: ![]() . Оно делится на 8. Следовательно, осталось доказать, что выражение
. Оно делится на 8. Следовательно, осталось доказать, что выражение ![]() делится на 6. Для этого нужно доказать, что оно делится на 2 и на 3.
делится на 6. Для этого нужно доказать, что оно делится на 2 и на 3.
а) Доказываем делимость на 2. Если k — чётное, то выражение делится на 2. Если k — нечётное, то его можно представить в виде ![]() , где
, где ![]() Тогда выражение для k принимает вид:
Тогда выражение для k принимает вид: ![]() . Это выражение также делится на 2.
. Это выражение также делится на 2.
б) Докажем делимость на 3. Если k делится на 3, то выражение делится на 3. Если k не делится на 3, то его можно представить в виде ![]() или
или ![]() , где
, где ![]() В первом случае выражение для k принимает вид:
В первом случае выражение для k принимает вид: ![]() . Последнее выражение делится на 3. Во втором случае выражение для k принимает вид:
. Последнее выражение делится на 3. Во втором случае выражение для k принимает вид: ![]() . Последнее выражение также делится на 3.
. Последнее выражение также делится на 3.
| 4. Найдите максимальное и минимальное значение выражения:
|
Задача легко решается с помощью такого мощного понятия, как производная функции. Однако, поступающие в 10 класс школьники с этим понятием, к сожалению, не знакомы. Поэтому придётся «изобретать» другое решение.
Заметим сразу, что выражение, стоящее в знаменателе всегда положительно, поскольку коэффициент при ![]() положителен, а дискриминант соответствующего квадратного уравнения отрицателен. Заметим также, что выражение принимает отрицательные значения при
положителен, а дискриминант соответствующего квадратного уравнения отрицателен. Заметим также, что выражение принимает отрицательные значения при ![]() и положительные значения при
и положительные значения при ![]() . То есть минимальное значение будет отрицательным, а максимальное значение будет положительным.
. То есть минимальное значение будет отрицательным, а максимальное значение будет положительным.
а) Ищем максимальное значение. Рассмотрим следующее неравенство с параметром ![]() :
:
![]()
Будем искать минимальное значение a, при котором это неравенство выполняется для любых x. Это значение и будет являться максимальным значением данного выражения. Поскольку ![]() , то неравенство можно представить в виде:
, то неравенство можно представить в виде:
![]()
При ![]() последнее неравенство будет выполняться для всех x в том случае, если дискриминант соответствующего квадратного уравнения будет меньше или равен нулю. То есть при
последнее неравенство будет выполняться для всех x в том случае, если дискриминант соответствующего квадратного уравнения будет меньше или равен нулю. То есть при ![]() . Наименьшее из возможных значений значений a, которое удовлетворяет всем требуемым условиям, является число
. Наименьшее из возможных значений значений a, которое удовлетворяет всем требуемым условиям, является число ![]() . Это значение достигается в вершине соответствующей квадратичной функции, то есть при
. Это значение достигается в вершине соответствующей квадратичной функции, то есть при ![]() .
.
б) Рассуждая аналогично, находим, что наименьшее значение выражения равно ![]() .
.
Разбор заданий вступительного экзамена по математике в лицей «Вторая школа» представлен репетитором по математике в Москве, Сергеем Валерьевичем.

![Rendered by QuickLaTeX.com \[ \frac{3x^2-|2x+3|+2}{3|x|-1} = 0. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-74776803c3ce630a0ce7db9cd682f2ef_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases} xy = 4 \\ y^2 = x+2. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ea247cce86664d8f1d8eaad491d5551e_l3.png)