Набор во Вторую школу

Суббота, 20 июня, 2020

Каждый год десятки московских родителей с нетерпением ожидают, когда будет объявлен набор во Вторую школу. Их легко понять: обучение здесь – это шанс получить образование высокого качества. Среди учеников и выпускников это школы встречаются:

победители всероссийских и международных олимпиад;
студенты лучших российских вузов;
кандидаты и доктора наук;
лауреаты российских и международных премий;
и даже академики РАН и Британской академии наук.

Пока среди выпускников нет, пожалуй, только обладателей Нобелевской премии. Но у школы с такой историей, это, конечно, ещё впереди.

История лицея «Вторая школа»

В 1956 году на окраине Москвы открыли новую школу – самую обычную, общеобразовательную, просто №2. В.Ф. Овчинников, директор школы, уже тогда был гениальным педагогом и руководителем: не колеблясь, он отправился в Институт точной механики и вычислительной техники и договорился об организации обучения радиомонтажников на его базе. Это было впервые в городе. И новые ученики заполнили классы – сейчас бы их назвали продвинутыми. Спустя год уже директор института, которому понравился опыт сотрудничества, предложил обучать ещё и программистов. По тем временам это была неслыханная специальность. Так сформировался профиль школы – физико-математический. К слову, дальше ещё многие нововведения в школе сопровождались эпитетом «первый».

Отбор был жёстким, но в результате лучших детей стали учить лучшие педагоги. Среди них были настоящие ученые. Лучшее – всегда нестандартное. Нестандартной была и атмосфера в школе: она предполагала свободу мышления, свободу взглядов на происходящее в стране и в мире.

Сейчас лицей «Вторая школа» – это:

верхние строчки в рейтингах учебных заведений Москвы и России;
7 кандидатов наук и 2 доктора наук среди педагогов;
высокая конкурентоспособность выпускников на российском и международном уровне;
победы учащихся на всероссийских и международных предметных олимпиадах;
разнообразная внеурочная деятельность.

Высокие баллы на ЕГЭ и уверенное поступление в ведущие вузы сами собой разумеются.

Набор в лицей «Вторая школа»

Прием в лицей проводится во вновь открывающиеся 6 и 7 классы. В 8-11 классы может быть добор на свободные места, если такие появятся. При этом для поступления в 11 класс недостаточно только успешного прохождения вступительных испытаний: необходимы высокие результаты обучения за два предыдущих года и обязательно – призовые места в олимпиадах как минимум регионального уровня.

Вступительные испытания во все классы проходят в форме зачетов, без отметок. Первый незачет допускает повторное выполнение. Два незачета влекут за собой отстранение от участия в приемной кампании.

Для поступления в 6 и 7 классы требуется получить зачет по русскому языку и математике. Последний разбит на два уровня: базовая математика проверяется письменно, творческая – устно, в процессе решения нестандартных задач.

Для зачисления на вакантные места в 8 класс предусмотрены дополнительные испытания по профильной математике, где необходимо решить задачи по программе Лицея, и по физике. В 9-11 классе вместо творческой математики вводится алгебра.

Каждый зачет занимает от полутора до трех часов в зависимости от возраста учащихся. Заключительный этап испытаний – административное собеседование для выяснения мотивации и общего культурного уровня.

Учитывая, что набор в лицей «Вторая школа» всегда сопровождается сильнейшей конкуренцией самых способных детей, администрация предупреждает, что даже успешное прохождение конкурса – не гарантия зачисления, особенно в старших классах.

Учеба в лицее – это не только престижно и интересно. В первую очередь это сложно. Поэтому конкурс призван отобрать тех, кто способен оригинально мыслить, усердно трудиться и сотрудничать в коллективе. Одними школьными знаниями тут не обойтись. Скорее всего, понадобятся занятия с репетитором, предпочтительно индивидуальные.

Особенности набора во Вторую школу в условиях повышенной готовности

В обычном режиме вступительные экзамены во Вторую школу проходят очно. Однако, в 2020 году пандемия внесла свои коррективы. Все вступительные испытания проводятся дистанционно. Добор в 8-11 классы проходит в две волны. Вторая отложена на август. Регистрация на сайте лицея уже открыта. Разумно расценивать это как возможность дополнительной подготовки, благо многие хорошие репетиторы давно перешли на дистанционный формат.

Я говорю школьников к вступительным экзаменам в этот лицей, в том числе работаю летом. Это очень удобно, если вы планируете поступать в лицей «Вторая школа» в рамках второй волны набора.

Экзамены обычно сложные, поэтому необходима серьёзная подготовка. Для примера приведу здесь разбор письменной части вступительного экзамена в 10 класс в 2020 году (первая волна).

Разбор варианта вступительного экзамена первой волны

Задание 1. Числа $x$ , $y$ , $z$ , $t$ образуют арифметическую прогрессии, а числа $x+4$ , $y+1$ , $z-1$ , $t-1$ образуют геометрическую прогрессию. Найдите $x$ , $y$ , $z$ , $t$ . (Члены прогрессий указаны в порядке возрастания).

Пусть разность арифметической прогрессии равна $d$ . Тогда арифметическая прогрессия имеет вид: $x$ , $x+d$ , $x+2d$ , $x+3d$ . Значит, геометрическая прогрессия имеет вид: $x+4$ , $x+d+1$ , $x+2d-1$ , $x+3d-1$ . При этом среди членов этой геометрической прогрессии нет нулевых.

Тогда имеет место равенство: $(x+d+1)^2=(x+4)(x+2d-1)$ , из которого после упрощения получаем, что $d^2-6d+5=x$ . Тогда члены геометрической прогрессии можно представить в следующем виде:

$1:\, d^2-6d+9 = (d-3)^2$

$2:\, d^2-5d+6 = (d-2)(d-3)$

$3:\, d^2-4d+4 = (d-2)^2$

$4:\, d^2-3d+4$

Тогда имеет место равенство:

$(d-2)^4=(d-2)(d-3)(d^2-3d+4)$

Поскольку $d\ne 2$ (иначе 2-й и 2-й члены геометрической прогрессии нулевые, а два других отличны от нуля, что невозможно) получаем:

$(d-2)^3=(d-3)(d^2-3d+4)$

$d^2-6d+8=0$

Последнее уравнение имеет два корня: $d_1 = 2$ , который не подходит, и $d_2 = 4$ , который подходит. Тогда $x=-3$ , $y = 1$ , $z = 5$ и $t = 9$ .

Задание 2. Из города в село выходит автобус со скоростью V км/ч. Через 30 мин. следом за ним выезжает автомобиль со скоростью 40 км/ч, догоняет автобус, не доезжая до села, и возвращается обратно в город. Выясните, какой должна быть скорость автобуса, чтобы он прибыл в село раньше, чем автомобиль вернётся в город. Расстояние от города до села 30 км.

К моменту выезда автомобиля автобус проедет $\dfrac{1}{2}V$ км. Скорость сближения автомобиля и автобуса равна $40-V$ км/ч. Значит, автомобиль догонит автобус через $\dfrac{V}{2(40-V)}$ часов. Столько же времени он потратит на то, чтобы вернуться обратно в город. То есть общее время движения автомобиля составляет $\( \dfrac{V}{40-V}$ часов. Общее время движения автобуса составляет $\dfrac{30}{V}$ . Поскольку автомобиль выехал из города на полчаса раньше, то имеет место неравенство:

$\dfrac{30}{V}-\dfrac{1}{2}<\dfrac{V}{40-V}$

$\dfrac{(V-20)(V+120)}{V(V-40)}<0$

Решая полученное неравенство, получаем для $V>0$ окончательный ответ: $20<V<40$ .

Задание 3. Решите уравнение:

$\sqrt{\sqrt{x+2}+\sqrt{x-2}}=2\sqrt{\sqrt{x+2}-\sqrt{x-2}}+\sqrt{2}$

Заметим, что в области допустимых значений, то есть при $x\geqslant 2$ , верно равенство:

$\left(\sqrt{x+2}+\sqrt{x-2}\right)\left(\sqrt{x+2}-\sqrt{x-2}\right)=4$

Тогда исходное уравнение можно переписать в виде:

$\sqrt{\sqrt{x+2}+\sqrt{x-2}} = \dfrac{4}{\sqrt{\sqrt{x+2}+\sqrt{x-2}}} +\sqrt{2}$

Пусть $\sqrt{\sqrt{x+2}+\sqrt{x-2}} = t > 0$ . Тогда получаем уравнение $t=\dfrac{4}{t}+\sqrt{2}$ , откуда $t = 2\sqrt{2}$ .

Возвращаясь к исходной переменной, получаем следующее уравнение:

$\sqrt{x+2}+\sqrt{x-2} = 8$

В области допустимых значений можно возвести обе части полученного уравнения в квадрат:

$x+2+2\sqrt{(x+2)(x-2)}+x-2 = 64$

$\sqrt{x^2-4} = 32-x$

Для $32-x\geqslant 0$ после возведения в квадрат обеих частей полученного уравнения получаем:

$x^2-4 = x^2-64x+1024 \Leftrightarrow x = \dfrac{257}{16}$

Задание 4. Решите неравенство:

$|x^3-2x^2+2|\geqslant 2-3x$

Исходное неравенство равносильно следующей совокупности:

$\left[\begin{array}{l} x^3-2x^2+2\geqslant 2-3x \\ x^3-2x^2+2\leqslant 3x-2 \end{array}\Leftrightarrow \left[\begin{array}{l} x^3-2x^2+3x\geqslant 0 \\ x^3-2x^2-3x+4\leqslant 0 \end{array}$

Преобразуем неравенства к следующему виду:

$\left[\begin{array}{l} x(x^2-2x+3)\geqslant 0 \\ x^3-2x^2-3x+4\leqslant 0 \end{array}$

Обратим внимание, что $x^2-2x+3 = (x-1)^2+2> 0$ . Значит, первое неравенство в совокупности эквивалентно неравенству $x\geqslant 0$ .

Разложим левую часть второго неравенства на множители. Для этого заметим, что корнем многочлена, стоящего слева, является число 1. Значит, его можно нацело поделить на $x-1$ . Тогда получаем следующее неравенство:

$(x-1)(x^2-x-4)\leqslant 0$

Решаем его методом интервалов, в результате чего получаем: $x \in \left(-\infty;\dfrac{1-\sqrt{17}}{2}\right]\cup \left [1;\dfrac{1+\sqrt{17}}{2}\right]$ . Объединяем полученный результат с решением первого неравенства совокупности и получаем окончательный ответ.

Ответ: $x \in \left(-\infty;\dfrac{1-\sqrt{17}}{2}\right]\cup [0;+\infty)$

Задание 5. Найдите все значения параметра $a$ , при каждом из которых уравнение

$\left(\dfrac{x-1}{x^2+1}\right)^2-2a\dfrac{x-1}{x^2+1}+a^2-0.25 = 0$

имеет ровно три различных действительных корня.

Пусть $t = \dfrac{x-1}{x^2+1}$ . Тогда исходное уравнение принимает вид: $t^2-2at+a^2-\dfrac{1}{4} = 0$ . Дискриминант этого уравнения равен $D = 4a^2-4\left(a^2-\dfrac{1}{4}\right) = 1$ . Значит, его корни равны $t_1 = \dfrac{2a+1}{2}$ и $t_2 = \dfrac{2a-1}{2}$ .

Возвращаемся теперь к исходной переменной: $\dfrac{x-1}{x^2+1} = \dfrac{2a+1}{2}$ и $\dfrac{x-1}{x^2+1} = \dfrac{2a-1}{2}$ . Поскольку $x^2+1>0$ , то можно умножить обе части каждого из уравнений на это выражение. Тогда после упрощения мы придём к следующим уравнениям:

(1) $\begin{equation*} (2a+1)x^2-2x+2a+3=0 \end{equation*}$

(2) $\begin{equation*} (2a-1)x^2-2x+2a+1=0 \end{equation*}$

Тогда возможны следующие варианты, когда исходное уравнение имеет 3 различных действительных корня:

Уравнение (1) имеет 1 корень, а уравнение (2) имеет два различных корня, каждый из которых не равен корню уравнения (1).
Уравнение (2) имеет 1 корень, а уравнение (1) имеет два различных корня, каждый из которых не равен корню уравнения (1).

Уравнение (1) имеет единственный корень, если:

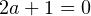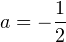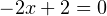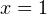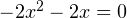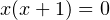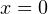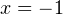При $2a+1=0$ , то есть при $a=-\dfrac{1}{2}$ . При этом получаем, что $-2x+2=0$ , то есть этот корень $x=1$ . Уравнение (2) при полученном значении параметра принимает вид $-2x^2-2x=0$ или $x(x+1) = 0$ , откуда получаем, что корни этого уравнения $x=0$ и $x=-1$ , то есть не совпадают в корнем первого уравнения. Этот случай подходит.
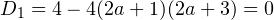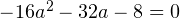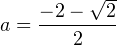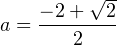Если $D_1 = 4-4(2a+1)(2a+3) = 0$ , то есть при $-16a^2-32a-8 = 0$ , откуда $a=\dfrac{-2-\sqrt{2}}{2}$ и $a=\dfrac{-2+\sqrt{2}}{2}$ . Для первого значения параметра уравнение (2) принимает вид: 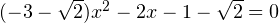$(-3-\sqrt{2})x^2-2x-1-\sqrt{2}=0$ . Дискриминант полученного уравнения отрицателен. Этот случай не подходит. Для второго значения параметра уравнение (2) принимает вид: 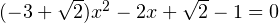$(-3+\sqrt{2})x^2-2x+\sqrt{2}-1=0$ . Дискриминант полученного уравнения положителен, оно имеет два различных корня. Убедимся, что ни один из них не совпадает с корнем уравнения (1). Действительно, корень уравнения (1) при рассматриваемом значении параметра равен: 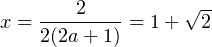$x = \dfrac{2}{2(2a+1)} = 1+\sqrt{2}$ . Прямой подстановкой убеждаемся, что это число не является корнем уравнения (2) при рассматриваемом значении параметра. Этот случай подходит.

Уравнение (2) имеет единственный корень, если:

При 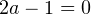$2a-1=0$ , то есть при 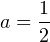$a=\dfrac{1}{2}$ . При этом получаем, что 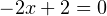$-2x+2=0$ , то есть этот корень 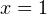$x=1$ . Но в этом случае уравнение (1) принимает вид: 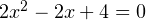$2x^2-2x+4=0$ . Последнее уравнение не имеет корней, поэтому этот вариант нам не подходит.
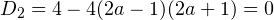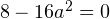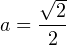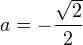Если $D_2 = 4-4(2a-1)(2a+1) = 0$ , то есть при $8-16a^2 = 0$ , откуда $a=\dfrac{\sqrt{2}}{2}$ и $a=-\dfrac{\sqrt{2}}{2}$ . Для первого значения параметра уравнение (1) принимает вид: 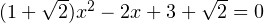$(1+\sqrt{2})x^2-2x+3+\sqrt{2}=0$ . Дискриминант полученного уравнения отрицателен. Этот случай не подходит. Для второго значения параметра уравнение (1) принимает вид: 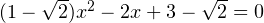$(1-\sqrt{2})x^2-2x+3-\sqrt{2}=0$ . Дискриминант полученного уравнения положителен, оно имеет два различных корня. Убедимся, что ни один из них не совпадает с корнем уравнения (2). Действительно, корень уравнения (2) при рассматриваемом значении параметра равен: 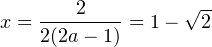$x = \dfrac{2}{2(2a-1)} = 1-\sqrt{2}$ . Прямой подстановкой убеждаемся, что это число не является корнем уравнения (1) при рассматриваемом значении параметра. Этот случай подходит.

Ответ: $a_1 = -\dfrac{1}{2}$ , $a_2 = -\dfrac{\sqrt{2}}{2}$ и $a_3 = \dfrac{-2+\sqrt{2}}{2}$ .

Задание 6. Решите уравнение:

$\left(x^2-x\right)^2-\dfrac{24(x-1)}{x-2}+12=0$

Приведём всё к общему знаменателю:

$\dfrac{x^2(x-1)^2(x-2)-24(x-1)+12(x-2)}{x-2}=0$

$\dfrac{x^2(x-1)^2(x-2)-12x}{x-2}=0$

$\dfrac{x(x(x-1)^2(x-2)-12)}{x-2}=0$

$\frac{x((x^2-2x+1)(x^2-2x)-12)}{x-2} = 0$

Для $x\ne 2$ получаем, что $x_1 = 0$ или $(x^2-2x+1)(x^2-2x)-12 = 0$ . Последнее уравнение решаем заменой $t = x^2-2x$ . Тогда $t^2+t-12 = 0$ , откуда $t_1 = -4$ и $t_2 = 3$ . Возвращаясь к исходной переменной, получаем, что $x^2-2x + 4 =0$ или $x^2-2x - 3 =0$ . Решения есть только у второго уравнения: $x_2 = 3$ и $x_3=-1$ .

Ответ: 0, -1, 3.

Задание 7. При каком значении параметра $b$ сумма

$\dfrac{x_1}{2x_2}+\dfrac{2x_2}{x_1}$

достигает своего наименьшего положительного значения, если $x_1$ и $x_2$ — корни уравнения $x^2-(2b+1)x+2b^2 = 0$ .

Преобразуем выражение к виду:

$\dfrac{x_1}{2x_2}+\dfrac{2x_2}{x_1} = \dfrac{x_1^2+4x_2^2}{2x_1x_2} =$

$= \dfrac{x_1^2-4x_1x_2+4x_2^2+4x_1x_2}{2x_1x_2} = \dfrac{(x_1-2x_2)^2+4x_1x_2}{2x_1x_2} =$

$=\dfrac{(x_1-2x_2)^2}{2x_1x_2}+2$

Так как $x_1x_2 = 2b^2 > 0$ , то в этом случае наименьшее положительное значение 2 достигается, если $x_1 = 2x_2$ . Тогда с учётом теоремы Виета для квадратного уравнения получаем следующую систему уравнений:

$\begin{cases}x_1+x_2=2b+1 \\ x_1x_2=2b^2 \\ x_1=2x_2 \end{cases}$

Поскольку $x_1=2x_2$ , то сумма $x_1+x_2 = 3x_2 = 2b+1$ , откуда находим, что $x_2 = \dfrac{2b+1}{3}$ . Тогда $x_1 = \dfrac{4b+2}{3}$ . Подставляем полученные выражения для $x_1$ и $x_2$ во второе уравнение системы и получаем следующее уравнение:

$\dfrac{4b+2}{3}\cdot \dfrac{2b+1}{3} = 2b^2$

$5b^2 -4b - 1 =0$

Последнее уравнение имеет 2 решения: $b_1 = 1$ и $b_2 = -\dfrac{1}{5}$ .

Ответ: $1$ и $-\dfrac{1}{5}$ .

Подготовка к набору во Вторую школу

Вот такие задания предлагались абитуриентам лицея на дистанционном вступительном экзамене в рамках набора во Вторую школу в этом году. Вторая волна вступительных экзаменов ожидается во второй половине августа, поэтому у вас всё ещё есть возможность подготовиться к этим экзаменам. И лучше всего это делать с репетитором. Я как раз занимаюсь такого рода подготовкой, в том числе работаю летом. С радостью готов организовать для вас занятия по подготовке к поступлению в лицей «Вторая школа». Обращайтесь! Мои контакты вы найдёте на этой странице.

Метки: алгебра, лицей вторая школа, подготовка к вступительным экзаменам с репетитором, решение задач по математике
Опубликовано в категории Методическая копилка | Комментарии к записи Набор во Вторую школу отключены

Набор во Вторую школу

История лицея «Вторая школа»

Набор в лицей «Вторая школа»

Особенности набора во Вторую школу в условиях повышенной готовности

Разбор варианта вступительного экзамена первой волны

Подготовка к набору во Вторую школу

Страницы

Понравился сайт?

Последние записи

Архив записей

Прочее