Считается, что чем больше различных решений существует у задачи, тем она интереснее с математический точки зрения. В этом отношении, задача, которую мы рассмотрим сегодня, является одной из наиболее интересных в школьном курсе геометрии. Она же, кстати, была предложена для решения в задании 24 модуля «Геометрия» демонстрационного варианта ОГЭ по математике в 2015 году. Так что попробуем решить её максимально возможным количеством способов, не выходящих за рамки школьного курса. Присылайте, пожалуйста, свои варианты решения в комментариях или на почту репетитора по математике и физике. С удовольствием опубликую их и поставлю ссылку на вашу анкету или сайт, если это необходимо.

Доказательство репетитора по математике и физике

I способ. Дополнительное построение.

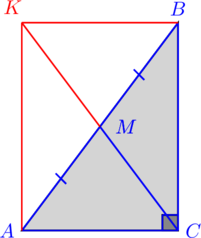
1. Проведем прямую через точку , параллельную прямой . Точку пересечения этой прямой с прямой обозначим буквой .

2. Тогда , так как они являются накрест лежащими при параллельных прямых , и секущей . Также , так как они вертикальные. Кроме того, по условию. Следовательно, по стороне и двум прилежащим к ней углам.

3. Следовательно, . То есть в четырехугольнике две стороны равны и параллельны. Следовательно, этот четырехугольник — параллелограмм. Кроме того, все углы этого параллелограмма прямые. Следовательно, — прямоугольник.

4. То есть , так как это диагонали данного прямоугольника. Кроме того, эти диагонали точкой пересечения делятся пополам, следовательно, .

II способ. Описать окружность.

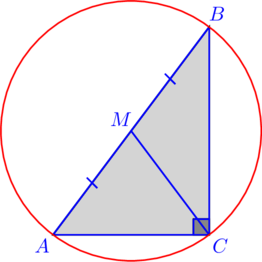
1. Опишем вокруг треугольника окружность. является диаметром этой окружности, поскольку — вписанный в эту окружность и должен опираться на полуокружность.

2. Следовательно, , где — радиус описанной окружности.

III способ. Решение «с конца».

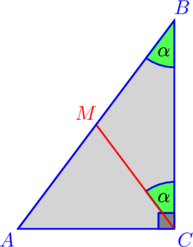
1. Проведем отрезок такой, что . Тогда — равнобедренный, а значит .

2. Кроме того, . Следовательно, — равнобедренный, а значит .

3. Следовательно, . Что и требовалось доказать.