Данную задачу прислала одна из читательниц моего блога с просьбой объяснить решение. Задача показалась мне достаточно интересной, поэтому я решил написать про неё отдельную маленькую статью. Итак, давайте вместе разберёмся с задачей и её решением.
| Точка |
Решение задачи сводится к построению окружностей, симметричных исходным относительно точки ![]() . На рисунке исходные окружности изображены сплошной синей линией, а построенные симметричные — пунктирной красной. Тогда искомая прямая
. На рисунке исходные окружности изображены сплошной синей линией, а построенные симметричные — пунктирной красной. Тогда искомая прямая ![]() легко получается из соображений симметрии, как показано на рисунке:
легко получается из соображений симметрии, как показано на рисунке:
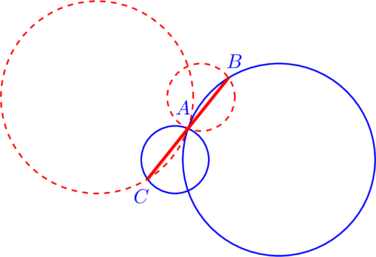
Как видите, задача интересна тем, что для её решения фактически не требуется глубоких знаний геометрии. Всё решается на основе здравого смысла и самых простых представлений о симметрии, поэтому решить её могут даже стопроцентные гуманитарии.
Присылайте свои интересные задачи, с удовольствием решим их вместе и опубликуем на страницах данного сайта. Удачи в обучении! Репетитор по математике в Москве в районе метро «Юго-Западная», Сергей Валерьевич.