 Практически с полной уверенностью можно сказать, что хотя бы одна задача на окружность обязательно встретится вам на ЕГЭ по математике профильного или базового уровня. В профильном варианте ЕГЭ такие задачи встречаются под номерами 6, 16 и, как эти ни странно, 18. Последнее задание ассоциируется обычно с параметрами, но если вы дочитаете эту статью до конца, то узнаете, как окружность может иногда помочь решить такого рода задания. Конечно, задачи на окружность в ЕГЭ могут попасться и в заданиях по стереометрии, но в этой статье речь пока пойдёт только о заданиях, связанных с планиметрией. В конце концов, первый шаг в освоении мастерства решения задач по стереометрии — это решение планиметрических задач.
Практически с полной уверенностью можно сказать, что хотя бы одна задача на окружность обязательно встретится вам на ЕГЭ по математике профильного или базового уровня. В профильном варианте ЕГЭ такие задачи встречаются под номерами 6, 16 и, как эти ни странно, 18. Последнее задание ассоциируется обычно с параметрами, но если вы дочитаете эту статью до конца, то узнаете, как окружность может иногда помочь решить такого рода задания. Конечно, задачи на окружность в ЕГЭ могут попасться и в заданиях по стереометрии, но в этой статье речь пока пойдёт только о заданиях, связанных с планиметрией. В конце концов, первый шаг в освоении мастерства решения задач по стереометрии — это решение планиметрических задач.
Все задания, которые мы сегодня рассмотрим, — это задания из реальных вариантов ЕГЭ по математике. Именно такого рода задания вам и предстоит решать на ЕГЭ, если вы к нему готовитесь. Так что дочитайте эту статью до конца. Знания, которые вы получите, обязательно пригодятся вам на экзамене.
| Задание 6. Внутри треугольника ABC взяли точку O такую, что она равноудалена от вершин треугольника. Угол BAC равен 62 |
Обратим сразу внимание на то, что поскольку точка O равноудалена от вершин треугольника, то она является центром описанной около него окружности. Интересно также отметить, что этот треугольник обязательно должен быть остроугольным. В противном случае центр описанной окружности должен был бы оказаться вне треугольника, а не внутри него, как у нас. Изобразим эту ситуацию на рисунке:
Ну и теперь, когда мы всё это понимаем, как же решить задачу? Для этого нужно знать так называемую теорему о вписанном угле, которая гласит, что градусная мера вписанного угла равна половине градусной меры дуги, на которую этот угол опирается. И ещё нужно знать, что градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Ну и если вы помните эти нехитрые факты, решение становится совсем простым. Ведь в нашем случае угол BAC как раз является вписанным. Значит градусная мера малой дуги BC равна 124![]() (вдвое больше самого вписанного угла). Ну а тогда искомая градусная мера центрального угла BOC равна тем же 124
(вдвое больше самого вписанного угла). Ну а тогда искомая градусная мера центрального угла BOC равна тем же 124![]() . И это наш ответ:
. И это наш ответ:
Следующие задания из ЕГЭ по математике, при решении которых вам могут потребоваться знания, связанные с темой «Окружность», встречаются уже во второй части этого экзамена. Разберём пару примеров.
| Задание 16. Треугольник ABC вписан в окружность. Через вершину C проведена касательная к окружности, пересекающая прямую BA в точке D, причём B лежит между A и D; AB = 7.5 и CD = а) Докажите, что BD = 2AB. б) Из вершин A и B на касательную CD опущены перпендикуляры, меньший из которых равен 9. Определите площадь трапеции, образованной этими перпендикулярами, стороной AB и отрезком касательной. |
а) Начнём с доказательства. Для этого изобразим ситуацию на рисунке:
Для доказательства используем теорему о касательной и секущей. Согласно этой теореме имеет место соотношение:
![]()
Пусть ![]() . Тогда записанное равенство принимает вид:
. Тогда записанное равенство принимает вид:
![Rendered by QuickLaTeX.com \[ \left(15\sqrt{\frac{3}{2}}\right)^2 = x\left(\frac{15}{2}+x\right)\Leftrightarrow \frac{15^2\cdot 3}{2} = x\left(\frac{15}{2}+x\right) \Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8805e720e2ef597cfc07e39df9039d69_l3.png)
![]()
Из последнего равенства видно, что один из корней уравнения: ![]() . Второй будет отрицательным. Это видно из теоремы Виета. Конкретно из того, что свободный член в первоначальном квадратном уравнении, если его записать в стандартном виде, будет отрицателен. То есть второй корень нам не подходит.
. Второй будет отрицательным. Это видно из теоремы Виета. Конкретно из того, что свободный член в первоначальном квадратном уравнении, если его записать в стандартном виде, будет отрицателен. То есть второй корень нам не подходит.
Итак, получается, что BD = 15, и это доказывает, что BD = 2AB
б) Проведём теперь перпендикуляры к касательной из точек A и B, меньший из которых равен 9, и найдём площадь трапеции, образовавшейся между этими перпендикулярами, отрезком AB и отрезком касательной, концами которого являются основания проведённых перпендикуляров:
Начнём с того, что треугольники FBD и EAD подобны по двум углам. Действительно, угол ADE у них общий, а углы AED и BFD равны, поскольку они оба прямые. Коэффициент подобия этих треугольников равен отношению AD:BD, то есть равен ![]() . То есть сторона AE равна
. То есть сторона AE равна ![]() . Таким образом мы нашли оба основания трапеции.
. Таким образом мы нашли оба основания трапеции.
Теперь давайте найдём длину FD. Сделать это не сложно. Для этого нужно воспользоваться теоремой Пифагора для прямоугольного треугольника BFD. Из этого находим, что FD = 12. Значит, вновь используя подобие треугольников FBD и EAD, можно найти, что ED = 18, а значит EF = 6. То есть мы нашли высоту нашей трапеции.
Теперь мы знает всё, что нужно для нахождения площади нашей трапеции. Итак, искомая площадь равна:
![]()
Это наш ответ.
Ну и ещё одно задание из профильного ЕГЭ по математике, где вам может встретиться окружность, как это ни странно, — это задание под номером 18. Традиционно это задание ассоциируется с параметрами, поэтому причём здесь геометрия с окружностями с первого взгляда не совсем понятно. Но посмотрите на решение следующего задания, и вы поймёте в чём тут суть дела.
| Задание 18. Найдите все значения параметра имеет единственное решение. |
Рассмотрим три случая:
1. При ![]() . В этом случае
. В этом случае ![]() , что невозможно ни при каких
, что невозможно ни при каких ![]() и
и ![]() , поскольку сумма квадратов действительных чисел не может быть отрицательной. То есть в этом случае решений у системы нет.
, поскольку сумма квадратов действительных чисел не может быть отрицательной. То есть в этом случае решений у системы нет.
2. При ![]() уравнение системы принимает вид
уравнение системы принимает вид ![]() , что возможно только в том случае, если оба выражения в скобках одновременно обращаются в нуль. То есть имеет место система:
, что возможно только в том случае, если оба выражения в скобках одновременно обращаются в нуль. То есть имеет место система:
![Rendered by QuickLaTeX.com \[ \begin{cases} x=a \\ y=2a \end{cases} \begin{cases} x=-2 \\ y=-4. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-0f83813f806f8c52ed7425b8c43142d0_l3.png)
Прямой подстановкой полученных значений в неравенство системы убеждаемся, что они ему удовлетворяют:
![]()
Значит вариант с ![]() нам подходит, система имеет единственное решение при этом значении параметра
нам подходит, система имеет единственное решение при этом значении параметра ![]() .
.
3. Рассмотрим теперь случай, когда ![]() . В этом случае задание допускает графическое решение. Первое неравенство с модулем можно заменить вот таким двойным неравенством:
. В этом случае задание допускает графическое решение. Первое неравенство с модулем можно заменить вот таким двойным неравенством: ![]() . Тогда исходную систему можно переписать в следующем виде:
. Тогда исходную систему можно переписать в следующем виде:
![Rendered by QuickLaTeX.com \[ \begin{cases} x+2y\geqslant -12\\ x+2y\leqslant 10\\ (x-a)^2+(y-2a)^2=2+a. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-97ab5580160bb5d4376e0db0f52e25ac_l3.png)
Или в более удобном виде:
![Rendered by QuickLaTeX.com \[ \begin{cases} y\geqslant -6-\frac{1}{2}x\\ y\leqslant 5-\frac{1}{2}x\\ (x-a)^2+(y-2a)^2=2+a. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-a8534b8b45dca742ee68c21baa5de5e4_l3.png)
Посмотрим на уравнение системы. Какую линию задаёт на координатной плоскости это уравнение при ![]() ? И вот здесь-то и появляется наша любимая окружность. Действительно, ведь этой уравнение окружности! Квадрат радиуса этой окружности равен
? И вот здесь-то и появляется наша любимая окружность. Действительно, ведь этой уравнение окружности! Квадрат радиуса этой окружности равен ![]() , а центр лежит в точке
, а центр лежит в точке ![]() , то есть где-то на прямой
, то есть где-то на прямой ![]() . На рисунке снизу она изображена красным цветом. При этом прямая
. На рисунке снизу она изображена красным цветом. При этом прямая ![]() перпендикулярна прямой
перпендикулярна прямой ![]() :
:
Это легко доказать, если рассмотреть треугольник, полученный между этими прямыми и осью OY. Длины сторон этого треугольника равны ![]() ,
, ![]() и
и ![]() (подробнее об этом смотрите в видео). Значит, по теореме, обратной теореме Пифагора, этот треугольник является прямоугольным.
(подробнее об этом смотрите в видео). Значит, по теореме, обратной теореме Пифагора, этот треугольник является прямоугольным.
Изобразим теперь, какую область на координатной плоскости задают первые два неравенства системы. Для этого изобразим ещё график функции ![]() (зелёная линия на рисунке снизу). Тогда выделенная на рисунке снизу область, заключённая между этими прямыми, и будет являться искомой.
(зелёная линия на рисунке снизу). Тогда выделенная на рисунке снизу область, заключённая между этими прямыми, и будет являться искомой.
Это даёт понять, что система имеет единственное решение в том случае, когда наша окружность внешним образом касается верхней границы заштрихованной области в точке B, как показано на рисунке:
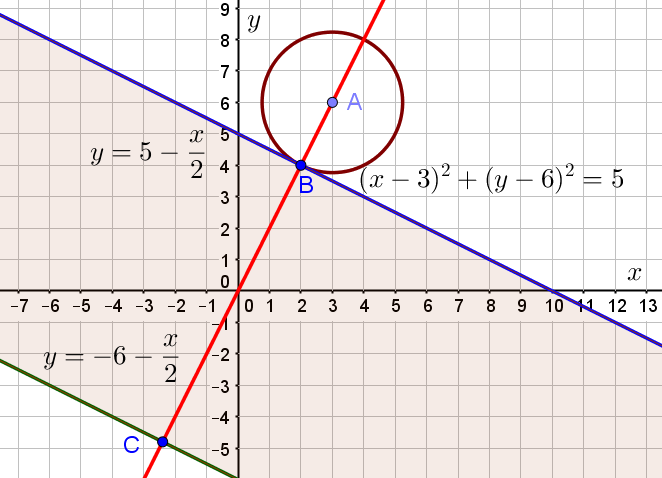
Эта ситуация реализуется, когда ![]() . Действительно, поскольку окружность касается области в точке B, то координаты этой точки должны удовлетворять уравнению окружности, то есть должно быть справедливо равенство:
. Действительно, поскольку окружность касается области в точке B, то координаты этой точки должны удовлетворять уравнению окружности, то есть должно быть справедливо равенство:
![]()
![]()
![]()
Подходит только первый корень, поскольку второй соответствует касанию окружности в точке B внутренним образом. То есть второй случай нам не подходит, так как в этом случае решений у системы будет бесконечно много, а не одно, как требуется в условии.
Итак, мы почти решили задачу. Остаётся открытым вопрос. Может ли подобная ситуация реализоваться в случае с касанием нашей окружности с выделенной областью в точке C внешним образом? Ответ на этот вопрос — нет. Почему? Потому что в этом случае координата ![]() центра окружности, а значит и значение параметра
центра окружности, а значит и значение параметра ![]() меньше -2. Но мы уже выяснили выше, что при
меньше -2. Но мы уже выяснили выше, что при ![]() решений у системы нет.
решений у системы нет.
Итак, ответ к этому заданию: ![]() .
.
В данной статье мы рассмотрели задачи на окружность, которые могут вам встретиться на ЕГЭ по математике. Они могли показаться вам сложными, особенно если вы только начали свою подготовку к предстоящему экзамену. Но на самом деле, для того, чтобы научиться их решать, не требуется ничего сверхъестественного. Нужно лишь желание, достаточное количество времени, ну и помощь грамотного наставника. Если кому-то из вас нужны занятия с репетитором для подготовки к предстоящему экзамену, пройдите по этой ссылке, там вы найдёте информацию обо мне и моих занятиях. Удачи вам в подготовке к экзамену!
Статью написал репетитор по математике для подготовки к ЕГЭ, Сергей Валерьевич
Понравилась статья? Тогда, возможно, вам будут интересны также следующие:
А как найти длину медианы треугольника, если известны его стороны?